How to check if two given line segments intersect?

Last Updated : 23 Jul, 2025

Given two line segments represented as a 3D vector points[][][], where each line segment i is defined by its endpoints stored in points[i][0] and points[i][1] (each containing 2 integers), your task is to determine if these two line segments intersect with each other.

Examples:

Input: points[][][] = [ [[1, 1], [10, 1]] , [[1, 2], [10, 2]] ]
Output: No
Explanation: The given line segments are parallel to each other.

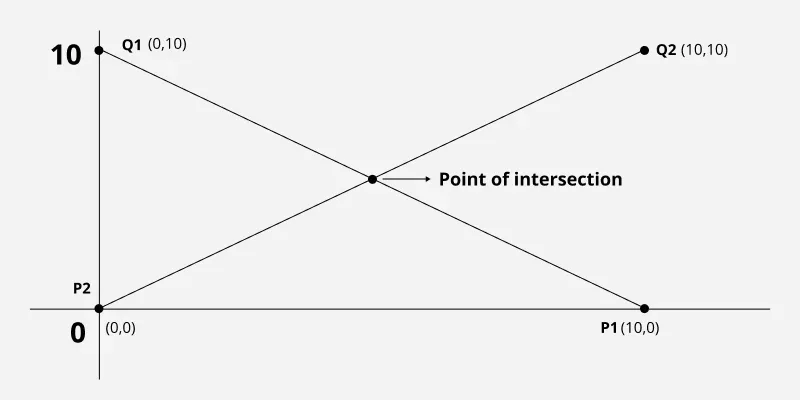
Input: points[][][] = [ [[10, 0], [0, 10]] , [[0, 0], [10, 10]] ]
Output: Yes
Explanation: The given line segments are mirror image of each other and intersects at middle point.

We are going to use the below concept of orientation to solve this problem.

Orientation of 3 Ordered Points

Orientation of an ordered triplet of points in the plane can be:
counterclockwise
clockwise
collinear
The following diagram shows different possible orientations of (a, b, c)
If orientation of (p1, p2, p3) is collinear, then orientation of (p3, p2, p1) is also collinear.
If orientation of (p1, p2, p3) is clockwise, then orientation of (p3, p2, p1) is counterclockwise and vice versa is also true.

Using Orientation of Lines - O(1) Time and O(1) Space

The idea is to use orientation of lines to determine whether they intersect or not. Two line segments [p1, q1] and [p2, q2] intersects if and only if one of the following two conditions is verified:
1. General Case:-
[p1, q1, p2] and [p1, q1, q2] have different orientations.
[p2, q2, p1] and [p2, q2, q1] have different orientations.
Following image contains examples of general case:
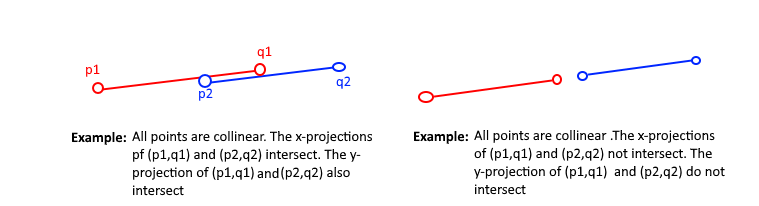
2. Special Case:
[p1, q1, p2], [p1, q1, q2], [p2, q2, p1], and [p2, q2, q1] are all collinear.
The x-projections of [p1, q1] and [p2, q2] intersect.
The y-projections of [p1, q1] and [p2, q2] intersect.
Following image contains examples of special case:

Approach:

The idea is to firstly find the four orientations required to analyze general and special cases. We've discussed an approach to find orientation of 3 ordered points in article Orientation of 3 Ordered points. Thereafter, check for the general case, if both the conditions are true, return true, else check for special case. Now, for special case, the points must be collinear and the point should on the line segment. To check if the point lies on line segment, check if the point lies between max and min of x and y coordinates.

C++

#include <bits/stdc++.h>
using namespace std;

// function to check if point q lies on line segment 'pr'
bool onSegment(vector<int>& p, vector<int>& q, vector<int>& r) {
    return (q[0] <= max(p[0], r[0]) && 
            q[0] >= min(p[0], r[0]) &&
            q[1] <= max(p[1], r[1]) && 
            q[1] >= min(p[1], r[1]));
}

// function to find orientation of ordered triplet (p, q, r)
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(vector<int>& p, vector<int>& q, vector<int>& r) {
    int val = (q[1] - p[1]) * (r[0] - q[0]) -
              (q[0] - p[0]) * (r[1] - q[1]);

    // collinear
    if (val == 0) return 0;

    // clock or counterclock wise
    // 1 for clockwise, 2 for counterclockwise
    return (val > 0) ? 1 : 2;
}


// function to check if two line segments intersect
bool doIntersect(vector<vector<vector<int>>>& points) {

    // find the four orientations needed
    // for general and special cases
    int o1 = orientation(points[0][0], points[0][1], points[1][0]);
    int o2 = orientation(points[0][0], points[0][1], points[1][1]);
    int o3 = orientation(points[1][0], points[1][1], points[0][0]);
    int o4 = orientation(points[1][0], points[1][1], points[0][1]);

    // general case
    if (o1 != o2 && o3 != o4)
        return true;

    // special cases
    // p1, q1 and p2 are collinear and p2 lies on segment p1q1
    if (o1 == 0 && 
    onSegment(points[0][0], points[1][0], points[0][1])) return true;

    // p1, q1 and q2 are collinear and q2 lies on segment p1q1
    if (o2 == 0 && 
    onSegment(points[0][0], points[1][1], points[0][1])) return true;

    // p2, q2 and p1 are collinear and p1 lies on segment p2q2
    if (o3 == 0 && 
    onSegment(points[1][0], points[0][0], points[1][1])) return true;

    // p2, q2 and q1 are collinear and q1 lies on segment p2q2 
    if (o4 == 0 && 
    onSegment(points[1][0], points[0][1], points[1][1])) return true;

    return false;
}

int main() {
    vector<vector<vector<int>>> points = 
    {{{1, 1}, {10, 1}}, {{1, 2}, {10, 2}}};

    if(doIntersect(points))
        cout << "Yes";
    else cout << "No";

    return 0;
}

Java

import java.util.*;

public class GfG {

    // function to check if point q lies on line segment 'pr'
    public static boolean onSegment(int[] p, int[] q, int[] r) {
        return (q[0] <= Math.max(p[0], r[0]) && 
                q[0] >= Math.min(p[0], r[0]) &&
                q[1] <= Math.max(p[1], r[1]) && 
                q[1] >= Math.min(p[1], r[1]));
    }

    // function to find orientation of ordered triplet (p, q, r)
    // 0 --> p, q and r are collinear
    // 1 --> Clockwise
    // 2 --> Counterclockwise
    public static int orientation(int[] p, int[] q, int[] r) {
        int val = (q[1] - p[1]) * (r[0] - q[0]) -
                  (q[0] - p[0]) * (r[1] - q[1]);

        if (val == 0) return 0;

        return (val > 0) ? 1 : 2;
    }

    // function to check if two line segments intersect
    public static boolean doIntersect(int[][][] points) {

        int o1 = orientation(points[0][0], points[0][1], points[1][0]);
        int o2 = orientation(points[0][0], points[0][1], points[1][1]);
        int o3 = orientation(points[1][0], points[1][1], points[0][0]);
        int o4 = orientation(points[1][0], points[1][1], points[0][1]);

        if (o1 != o2 && o3 != o4)
            return true;

        if (o1 == 0 &&
        onSegment(points[0][0], points[1][0], points[0][1])) return true;

        if (o2 == 0 &&
        onSegment(points[0][0], points[1][1], points[0][1])) return true;

        if (o3 == 0 &&
        onSegment(points[1][0], points[0][0], points[1][1])) return true;

        if (o4 == 0 &&
        onSegment(points[1][0], points[0][1], points[1][1])) return true;

        return false;
    }

    public static void main(String[] args) {
        int[][][] points = {
            { {1, 1}, {10, 1} },
            { {1, 2}, {10, 2} }
        };

        if (doIntersect(points))
            System.out.print("Yes");
        else
            System.out.print("No");
    }
}

Python

from collections import defaultdict

# function to check if point q lies on line segment 'pr'
def onSegment(p, q, r):
    return (q[0] <= max(p[0], r[0]) and q[0] >= min(p[0], r[0]) and
            q[1] <= max(p[1], r[1]) and q[1] >= min(p[1], r[1]))

# function to find orientation of ordered triplet (p, q, r)
# 0 --> p, q and r are collinear
# 1 --> Clockwise
# 2 --> Counterclockwise
def orientation(p, q, r):
    val = (q[1] - p[1]) * (r[0] - q[0]) - \
          (q[0] - p[0]) * (r[1] - q[1])

    # collinear
    if val == 0:
        return 0

    # clock or counterclock wise
    # 1 for clockwise, 2 for counterclockwise
    return 1 if val > 0 else 2


# function to check if two line segments intersect
def doIntersect(points):
    # find the four orientations needed
    # for general and special cases
    o1 = orientation(points[0][0], points[0][1], points[1][0])
    o2 = orientation(points[0][0], points[0][1], points[1][1])
    o3 = orientation(points[1][0], points[1][1], points[0][0])
    o4 = orientation(points[1][0], points[1][1], points[0][1])

    # general case
    if o1 != o2 and o3 != o4:
        return True

    # special cases
    # p1, q1 and p2 are collinear and p2 lies on segment p1q1
    if o1 == 0 and onSegment(points[0][0], points[1][0], points[0][1]):
        return True

    # p1, q1 and q2 are collinear and q2 lies on segment p1q1
    if o2 == 0 and onSegment(points[0][0], points[1][1], points[0][1]):
        return True

    # p2, q2 and p1 are collinear and p1 lies on segment p2q2
    if o3 == 0 and onSegment(points[1][0], points[0][0], points[1][1]):
        return True

    # p2, q2 and q1 are collinear and q1 lies on segment p2q2 
    if o4 == 0 and onSegment(points[1][0], points[0][1], points[1][1]):
        return True

    return False


if __name__ == "__main__":
    points = [[[1, 1], [10, 1]], [[1, 2], [10, 2]]]
    if doIntersect(points):
        print("Yes")
    else:
        print("No")

using System;
using System.Collections.Generic;

public class GfG {

    // function to check if point q lies on line segment 'pr'
    public static bool onSegment(List<int> p, List<int> q, List<int> r) {
        return (q[0] <= Math.Max(p[0], r[0]) && 
                q[0] >= Math.Min(p[0], r[0]) &&
                q[1] <= Math.Max(p[1], r[1]) && 
                q[1] >= Math.Min(p[1], r[1]));
    }

    // function to find orientation of ordered triplet (p, q, r)
    // 0 --> p, q and r are collinear
    // 1 --> Clockwise
    // 2 --> Counterclockwise
    public static int orientation(List<int> p, List<int> q, List<int> r) {
        int val = (q[1] - p[1]) * (r[0] - q[0]) -
                  (q[0] - p[0]) * (r[1] - q[1]);

        // collinear
        if (val == 0) return 0;

        // clock or counterclock wise
        // 1 for clockwise, 2 for counterclockwise
        return (val > 0) ? 1 : 2;
    }


    // function to check if two line segments intersect
    public static bool doIntersect(List<List<List<int>>> points) {

        // find the four orientations needed
        // for general and special cases
        int o1 = orientation(points[0][0], points[0][1], points[1][0]);
        int o2 = orientation(points[0][0], points[0][1], points[1][1]);
        int o3 = orientation(points[1][0], points[1][1], points[0][0]);
        int o4 = orientation(points[1][0], points[1][1], points[0][1]);

        // general case
        if (o1 != o2 && o3 != o4)
            return true;

        // special cases
        // p1, q1 and p2 are collinear and p2 lies on segment p1q1
        if (o1 == 0 &&
        onSegment(points[0][0], points[1][0], points[0][1])) return true;

        // p1, q1 and q2 are collinear and q2 lies on segment p1q1
        if (o2 == 0 &&
        onSegment(points[0][0], points[1][1], points[0][1])) return true;

        // p2, q2 and p1 are collinear and p1 lies on segment p2q2
        if (o3 == 0 &&
        onSegment(points[1][0], points[0][0], points[1][1])) return true;

        // p2, q2 and q1 are collinear and q1 lies on segment p2q2 
        if (o4 == 0 &&
        onSegment(points[1][0], points[0][1], points[1][1])) return true;

        return false;
    }

    public static void Main() {
        List<List<List<int>>> points = new List<List<List<int>>> {
            new List<List<int>> { new List<int> {1, 1}, 
                                new List<int> {10, 1} },
            new List<List<int>> { new List<int> {1, 2}, 
                                new List<int> {10, 2} }
        };

        if (doIntersect(points))
            Console.Write("Yes");
        else
            Console.Write("No");
    }
}

JavaScript

// function to check if point q lies on line segment 'pr'
function onSegment(p, q, r) {
    return (q[0] <= Math.max(p[0], r[0]) && 
            q[0] >= Math.min(p[0], r[0]) &&
            q[1] <= Math.max(p[1], r[1]) &&
            q[1] >= Math.min(p[1], r[1]));
}

    // function to find orientation of ordered triplet (p, q, r)
    // 0 --> p, q and r are collinear
    // 1 --> Clockwise
    // 2 --> Counterclockwise
function orientation(p, q, r) {
    let val = (q[1] - p[1]) * (r[0] - q[0]) -
              (q[0] - p[0]) * (r[1] - q[1]);

    // collinear
    if (val === 0) return 0;

    // clock or counterclock wise
    // 1 for clockwise, 2 for counterclockwise
    return (val > 0) ? 1 : 2;
}


// function to check if two line segments intersect
function doIntersect(points) {

    // find the four orientations needed
    // for general and special cases
    let o1 = orientation(points[0][0], points[0][1], points[1][0]);
    let o2 = orientation(points[0][0], points[0][1], points[1][1]);
    let o3 = orientation(points[1][0], points[1][1], points[0][0]);
    let o4 = orientation(points[1][0], points[1][1], points[0][1]);

    // general case
    if (o1 !== o2 && o3 !== o4)
        return true;

    // special cases
    // p1, q1 and p2 are collinear and p2 lies on segment p1q1
    if (o1 === 0 &&
    onSegment(points[0][0], points[1][0], points[0][1])) return true;

    // p1, q1 and q2 are collinear and q2 lies on segment p1q1
    if (o2 === 0 &&
    onSegment(points[0][0], points[1][1], points[0][1])) return true;

    // p2, q2 and p1 are collinear and p1 lies on segment p2q2
    if (o3 === 0 &&
    onSegment(points[1][0], points[0][0], points[1][1])) return true;

    // p2, q2 and q1 are collinear and q1 lies on segment p2q2 
    if (o4 === 0 &&
    onSegment(points[1][0], points[0][1], points[1][1])) return true;

    return false;
}

let points = [[[1, 1], [10, 1]], [[1, 2], [10, 2]]];
if (doIntersect(points))
    console.log("Yes");
else
    console.log("No");

Output

No

Time Complexity: O(1)
Space Complexity: O(1)

Analysis of Algorithms

kartik

Improve

Article Tags :

Practice Tags :

How to check if two given line segments intersect?

Orientation of 3 Ordered Points

Using Orientation of Lines - O(1) Time and O(1) Space

Similar Reads

Basics & Prerequisites

Data Structures

Algorithms

Advanced

Interview Preparation

Practice Problem

Thank You!

What kind of Experience do you want to share?