Dial's Algorithm (Optimized Dijkstra for small range weights)
Given a weighted Graph and a source vertex, the task is to find the shortest paths from the source node to all other vertices.
Example:
Input : n = 9, src = 0
Output : 0 4 12 19 21 11 9 8 14
We have learned about how to find the shortest path from a given source vertex to all other vertex using Dijkstra's shortest path algorithm with the Time Complexity of O(E log V) in this article.
Can we optimize Dijkstra's shortest path algorithm to work better than O(E log V) if the maximum weight is small (or the range of edge weights is small)?
For example, in the above diagram, the maximum weight is 14. Many times the range of weights on edges is in a small range (i.e. all edge weights can be mapped to 0, 1, 2.. W where W is a small number). In that case, Dijkstra’s algorithm can be modified by using different data structures, and buckets, which is called dial implementation of Dijkstra's algorithm. time complexity is O(E + WV) where W is the maximum weight on any edge of the graph, so we can see that, if W is small then this implementation runs much faster than the traditional algorithm.
The following are important observations.
- The maximum distance between any two nodes can be at max w(V – 1) (w is maximum edge weight and we can have at max V-1 edges between two vertices).
- In the Dijkstra algorithm, distances are finalized in non-decreasing, i.e., the distance of the closer (to given source) vertices is finalized before the distant vertices.
Approach:
The idea is to use bucket based optimization for Dijkstra's algorithm when edge weights are small integers. Instead of using a priority queue, we create buckets for each possible distance value and process nodes in distance order by iterating through buckets sequentially.


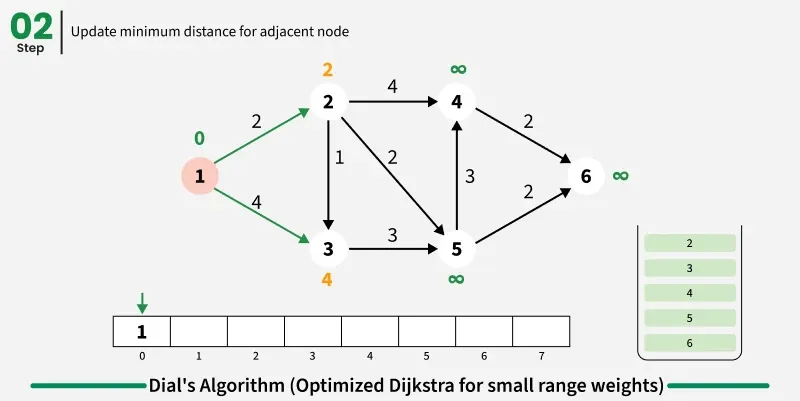

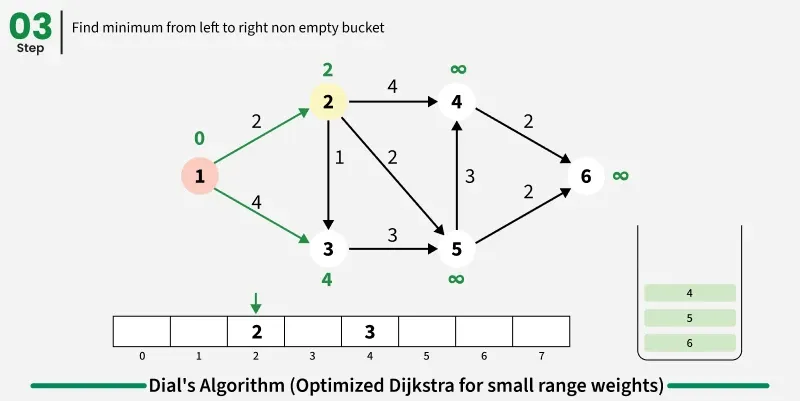

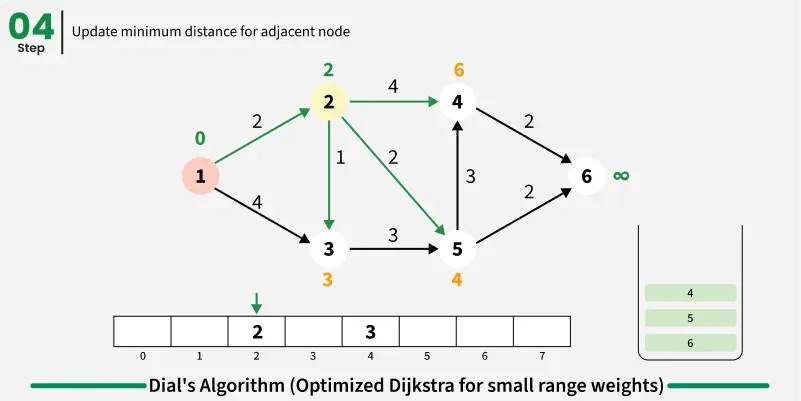

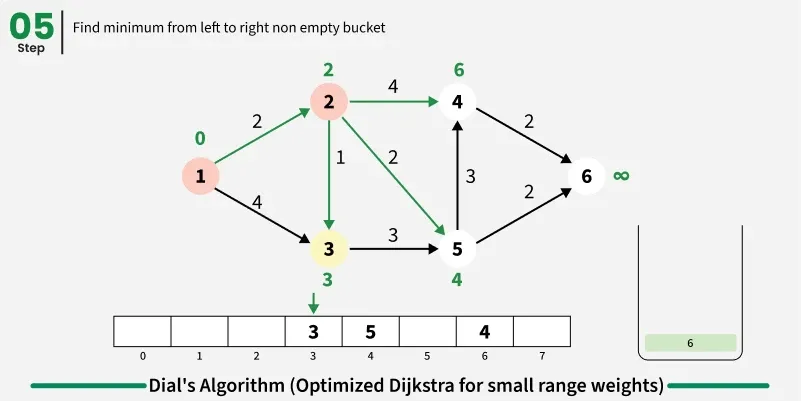

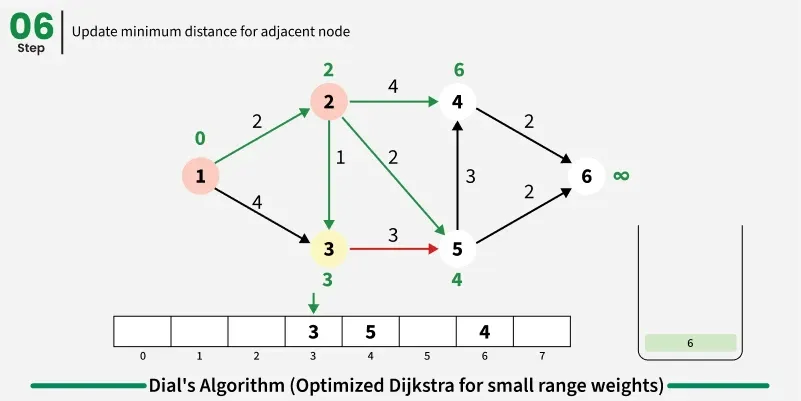

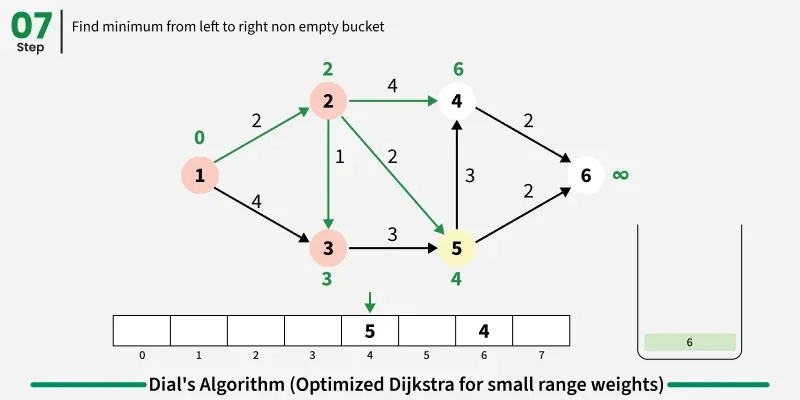

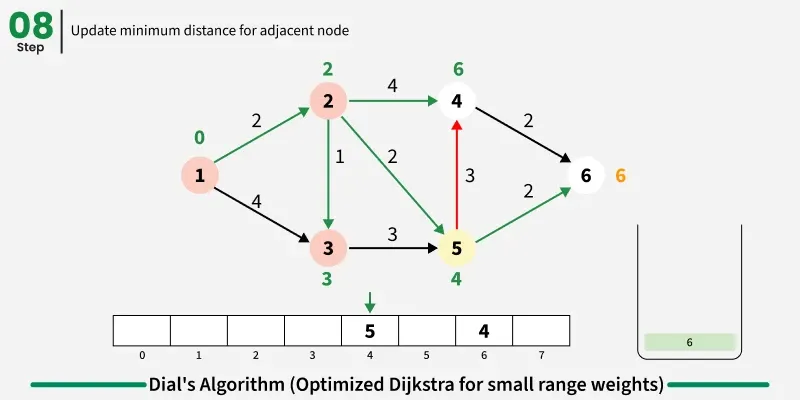

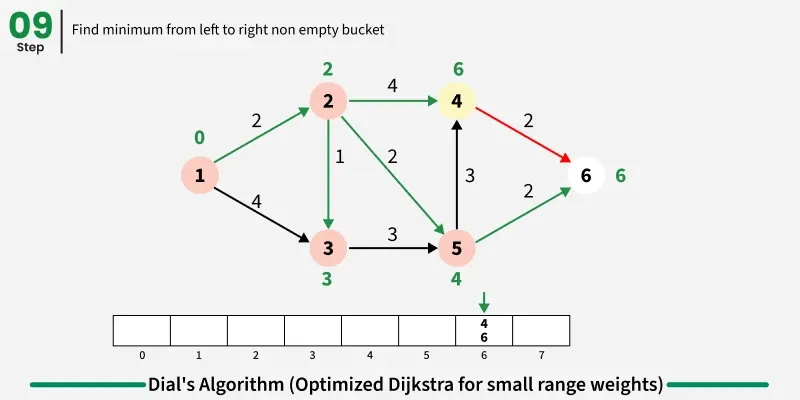

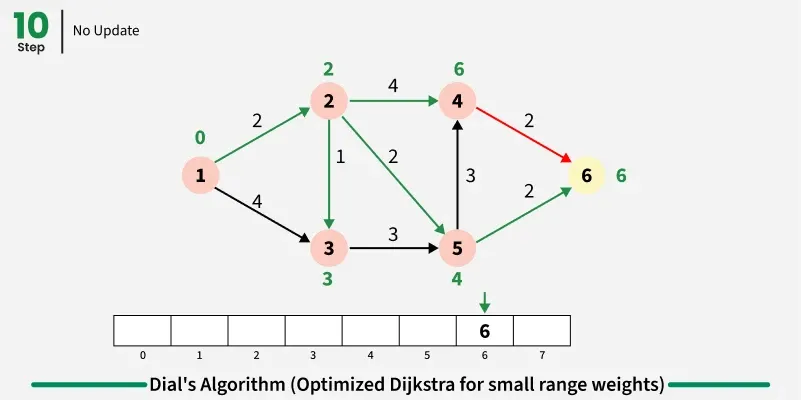

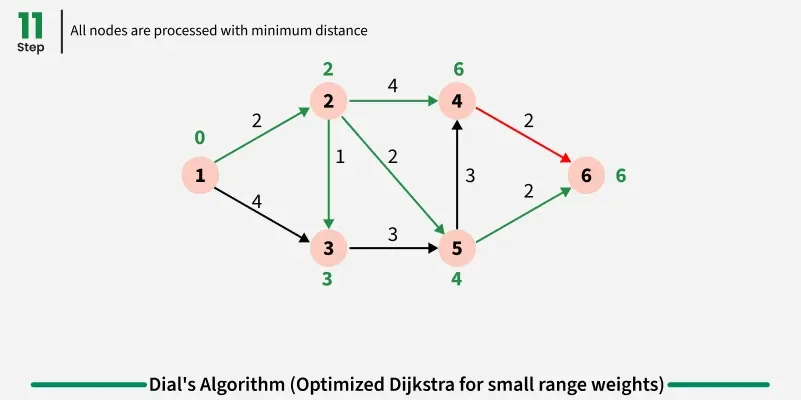

Step by step approach:
- Create buckets equal to maximum possible distance and initialize source distance as zero in first bucket.
- Iterate through buckets sequentially and process all nodes in current bucket:
- For each node, examine all adjacent nodes and calculate new distance through current node.
- If shorter path found, remove node from its current bucket and place in bucket corresponding to new distance.
// C++ program to find Shortest Path using Dial's Algorithm
#include <bits/stdc++.h>
using namespace std;
// Function to find Shortest Path
vector<int> shortestPath(int n, int src, vector<vector<int>> &edges) {
vector<vector<vector<int>>> adj(n);
int maxWeight = 0;
// Build adjacency list and find maximum weight
for (auto e: edges) {
adj[e[0]].push_back({e[1], e[2]});
adj[e[1]].push_back({e[0], e[2]});
maxWeight = max(maxWeight, e[2]);
}
// Initialize distance array
vector<int> dist(n, INT_MAX);
dist[src] = 0;
// Create buckets for distances
int maxDist = (n - 1) * maxWeight;
vector<unordered_set<int>> buckets(maxDist + 1);
// Add source to bucket 0
buckets[0].insert(src);
// Process buckets in order
for (int d = 0; d <= maxDist; d++) {
// Process all nodes in current bucket
while (!buckets[d].empty()) {
int u = *buckets[d].begin();
buckets[d].erase(buckets[d].begin());
// Skip if we already found a better path
if (d > dist[u]) continue;
// Process all adjacent nodes
for (auto& edge : adj[u]) {
int v = edge[0];
int weight = edge[1];
int newDist = dist[u] + weight;
// If shorter path found
if (newDist < dist[v]) {
// Remove from old bucket if it was there
if (dist[v] != INT_MAX) {
buckets[dist[v]].erase(v);
}
// Update distance and add to new bucket
dist[v] = newDist;
buckets[newDist].insert(v);
}
}
}
}
return dist;
}
int main() {
int n = 9;
int src = 0;
vector<vector<int>> edges = {
{0, 1, 4},
{0, 7, 8},
{1, 2, 8},
{1, 7, 11},
{2, 3, 7},
{2, 8, 2},
{3, 4, 9},
{3, 5, 14},
{4, 5, 10},
{5, 6, 2},
{6, 7, 1},
{6, 8, 6},
{7, 8, 7}
};
vector<int> res = shortestPath(n, src, edges);
for (auto val : res) {
cout << val << " ";
}
cout << endl;
return 0;
}
// Java program to find Shortest Path using Dial's Algorithm
import java.util.*;
class GfG {
// Function to find Shortest Path
static int[] shortestPath(int n, int src, int[][] edges) {
ArrayList<ArrayList<ArrayList<Integer>>> adj = new ArrayList<>();
int maxWeight = 0;
// Build adjacency list and find maximum weight
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] e : edges) {
ArrayList<Integer> edge1 = new ArrayList<>();
edge1.add(e[1]);
edge1.add(e[2]);
adj.get(e[0]).add(edge1);
ArrayList<Integer> edge2 = new ArrayList<>();
edge2.add(e[0]);
edge2.add(e[2]);
adj.get(e[1]).add(edge2);
maxWeight = Math.max(maxWeight, e[2]);
}
// Initialize distance array
int[] dist = new int[n];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[src] = 0;
// Create buckets for distances
int maxDist = (n - 1) * maxWeight;
ArrayList<HashSet<Integer>> buckets = new ArrayList<>(maxDist + 1);
for (int i = 0; i <= maxDist; i++) {
buckets.add(new HashSet<>());
}
// Add source to bucket 0
buckets.get(0).add(src);
// Process buckets in order
for (int d = 0; d <= maxDist; d++) {
// Process all nodes in current bucket
while (!buckets.get(d).isEmpty()) {
int u = buckets.get(d).iterator().next();
buckets.get(d).remove(u);
// Skip if we already found a better path
if (d > dist[u]) continue;
// Process all adjacent nodes
for (ArrayList<Integer> edge : adj.get(u)) {
int v = edge.get(0);
int weight = edge.get(1);
int newDist = dist[u] + weight;
// If shorter path found
if (newDist < dist[v]) {
// Remove from old bucket if it was there
if (dist[v] != Integer.MAX_VALUE) {
buckets.get(dist[v]).remove(v);
}
// Update distance and add to new bucket
dist[v] = newDist;
buckets.get(newDist).add(v);
}
}
}
}
return dist;
}
public static void main(String[] args) {
int n = 9;
int src = 0;
int[][] edges = {
{0, 1, 4},
{0, 7, 8},
{1, 2, 8},
{1, 7, 11},
{2, 3, 7},
{2, 8, 2},
{3, 4, 9},
{3, 5, 14},
{4, 5, 10},
{5, 6, 2},
{6, 7, 1},
{6, 8, 6},
{7, 8, 7}
};
int[] res = shortestPath(n, src, edges);
for (int val : res) {
System.out.print(val + " ");
}
System.out.println();
}
}
# Python program to find Shortest Path using Dial's Algorithm
import sys
from collections import defaultdict
def shortestPath(n, src, edges):
adj = [[] for _ in range(n)]
maxWeight = 0
# Build adjacency list and find maximum weight
for e in edges:
adj[e[0]].append([e[1], e[2]])
adj[e[1]].append([e[0], e[2]])
maxWeight = max(maxWeight, e[2])
# Initialize distance array
dist = [sys.maxsize] * n
dist[src] = 0
# Create buckets for distances
maxDist = (n - 1) * maxWeight
buckets = defaultdict(set)
# Add source to bucket 0
buckets[0].add(src)
# Process buckets in order
for d in range(maxDist + 1):
# Process all nodes in current bucket
while d in buckets and buckets[d]:
u = buckets[d].pop()
# Skip if we already found a better path
if d > dist[u]:
continue
# Process all adjacent nodes
for edge in adj[u]:
v, weight = edge[0], edge[1]
newDist = dist[u] + weight
# If shorter path found
if newDist < dist[v]:
# Remove from old bucket if it was there
if dist[v] != sys.maxsize:
buckets[dist[v]].discard(v)
# Update distance and add to new bucket
dist[v] = newDist
buckets[newDist].add(v)
return dist
if __name__ == "__main__":
n = 9
src = 0
edges = [
[0, 1, 4],
[0, 7, 8],
[1, 2, 8],
[1, 7, 11],
[2, 3, 7],
[2, 8, 2],
[3, 4, 9],
[3, 5, 14],
[4, 5, 10],
[5, 6, 2],
[6, 7, 1],
[6, 8, 6],
[7, 8, 7]
]
res = shortestPath(n, src, edges)
for val in res:
print(val, end=" ")
print()
// C# program to find Shortest Path using Dial's Algorithm
using System;
using System.Collections.Generic;
class GfG {
// Function to find Shortest Path
static int[] shortestPath(int n, int src, int[][] edges) {
List<List<List<int>>> adj = new List<List<List<int>>>();
int maxWeight = 0;
// Build adjacency list and find maximum weight
for (int i = 0; i < n; i++) {
adj.Add(new List<List<int>>());
}
foreach (int[] e in edges) {
adj[e[0]].Add(new List<int> {e[1], e[2]});
adj[e[1]].Add(new List<int> {e[0], e[2]});
maxWeight = Math.Max(maxWeight, e[2]);
}
// Initialize distance array
int[] dist = new int[n];
Array.Fill(dist, int.MaxValue);
dist[src] = 0;
// Create buckets for distances
int maxDist = (n - 1) * maxWeight;
List<HashSet<int>> buckets = new List<HashSet<int>>(maxDist + 1);
for (int i = 0; i <= maxDist; i++) {
buckets.Add(new HashSet<int>());
}
// Add source to bucket 0
buckets[0].Add(src);
// Process buckets in order
for (int d = 0; d <= maxDist; d++) {
// Process all nodes in current bucket
while (buckets[d].Count > 0) {
int u = 0;
foreach (int node in buckets[d]) {
u = node;
break;
}
buckets[d].Remove(u);
// Skip if we already found a better path
if (d > dist[u]) continue;
// Process all adjacent nodes
foreach (List<int> edge in adj[u]) {
int v = edge[0];
int weight = edge[1];
int newDist = dist[u] + weight;
// If shorter path found
if (newDist < dist[v]) {
// Remove from old bucket if it was there
if (dist[v] != int.MaxValue) {
buckets[dist[v]].Remove(v);
}
// Update distance and add to new bucket
dist[v] = newDist;
buckets[newDist].Add(v);
}
}
}
}
return dist;
}
static void Main() {
int n = 9;
int src = 0;
int[][] edges = new int[][] {
new int[] {0, 1, 4},
new int[] {0, 7, 8},
new int[] {1, 2, 8},
new int[] {1, 7, 11},
new int[] {2, 3, 7},
new int[] {2, 8, 2},
new int[] {3, 4, 9},
new int[] {3, 5, 14},
new int[] {4, 5, 10},
new int[] {5, 6, 2},
new int[] {6, 7, 1},
new int[] {6, 8, 6},
new int[] {7, 8, 7}
};
int[] res = shortestPath(n, src, edges);
foreach (int val in res) {
Console.Write(val + " ");
}
Console.WriteLine();
}
}
// Js program to find Shortest Path using Dial's Algorithm
function shortestPath(n, src, edges) {
const adj = Array.from({length: n}, () => []);
let maxWeight = 0;
// Build adjacency list and find maximum weight
for (const e of edges) {
adj[e[0]].push([e[1], e[2]]);
adj[e[1]].push([e[0], e[2]]);
maxWeight = Math.max(maxWeight, e[2]);
}
// Initialize distance array
const dist = new Array(n).fill(Infinity);
dist[src] = 0;
// Create buckets for distances
const maxDist = (n - 1) * maxWeight;
const buckets = Array.from({length: maxDist + 1}, () => new Set());
// Add source to bucket 0
buckets[0].add(src);
// Process buckets in order
for (let d = 0; d <= maxDist; d++) {
// Process all nodes in current bucket
while (buckets[d].size > 0) {
const u = buckets[d].values().next().value;
buckets[d].delete(u);
// Skip if we already found a better path
if (d > dist[u]) continue;
// Process all adjacent nodes
for (const edge of adj[u]) {
const [v, weight] = edge;
const newDist = dist[u] + weight;
// If shorter path found
if (newDist < dist[v]) {
// Remove from old bucket if it was there
if (dist[v] !== Infinity) {
buckets[dist[v]].delete(v);
}
// Update distance and add to new bucket
dist[v] = newDist;
buckets[newDist].add(v);
}
}
}
}
return dist;
}
const n = 9;
const src = 0;
const edges = [
[0, 1, 4],
[0, 7, 8],
[1, 2, 8],
[1, 7, 11],
[2, 3, 7],
[2, 8, 2],
[3, 4, 9],
[3, 5, 14],
[4, 5, 10],
[5, 6, 2],
[6, 7, 1],
[6, 8, 6],
[7, 8, 7]
];
const res = shortestPath(n, src, edges);
console.log(res.join(' '));
Output
0 4 12 19 21 11 9 8 14
Time Complexity: O(V + E + W×V), where W is the maximum weight of an edge.
Space Complexity: O(V + W×V) for storing buckets and adjacency list.
Advantages:
- Dial's algorithm can be much faster than Dijkstra's algorithm for graphs with small range weights.
- It is easy to implement and modify from Dijkstra's algorithm.
Disadvantages:
- Dial's algorithm is only applicable when the range of the edge weights is small. For graphs with large range weights, Dijkstra's algorithm may be faster.
