Sliding Window Technique

Last Updated : 20 May, 2025

Sliding Window Technique is a method used to solve problems that involve subarray or substring or window.

The main idea is to use the results of previous window to do computations for the next window.
This technique is commonly used in algorithms like finding subarrays with a specific sum, finding the longest substring with unique characters, or solving problems that require a fixed-size window to process elements efficiently.

Table of Content

Example Problem - Maximum Sum of a Subarray with K Elements

Given an array and an integer k, we need to calculate the maximum sum of a subarray having size exactly k.

Input : arr[] = {100, 200, 300, 400}, k = 2
Output : 700
We get maximum sum by considering the subarray [300, 400]
Input : arr[] = {1, 4, 2, 10, 23, 3, 1, 0, 20}, k = 4
Output : 39
We get maximum sum by adding subarray {4, 2, 10, 23} of size 4.
Input : arr[] = {2, 3}, k = 3
Output : Invalid
There is no subarray of size 3 as size of whole array is 2.

Naive Approach - O(n k) Time and O(1) Space

We run two nest loops and compute sums of all subarrays of size k

C++

#include <iostream>
#include <vector>
#include <climits>

using namespace std;

// Returns maximum sum in a subarray of size k.
int maxSum(vector<int>& arr, int k) {
    int n = arr.size();
    int max_sum = INT_MIN;

    // Consider all blocks starting with i
    for (int i = 0; i <= n - k; i++) {
        int current_sum = 0;

        // Calculate sum of current subarray of size k
        for (int j = 0; j < k; j++)
            current_sum += arr[i + j];

        // Update result if required
        max_sum = max(current_sum, max_sum);
    }

    return max_sum;
}

// Driver code
int main() {
    vector<int> arr = {1, 4, 2, 10, 2, 3, 1, 0, 20};
    int k = 4;

    cout << maxSum(arr, k) << endl;
    return 0;
}

// O(n*k) solution for finding maximum sum of
// a subarray of size k
#include <limits.h>
#include <math.h>
#include <stdio.h>

// Find maximum between two numbers.
int max(int num1, int num2)
{
    return (num1 > num2) ? num1 : num2;
}

// Returns maximum sum in a subarray of size k.
int maxSum(int arr[], int n, int k)
{
    // Initialize result
    int max_sum = INT_MIN;

    // Consider all blocks starting with i.
    for (int i = 0; i < n - k + 1; i++) {
        int current_sum = 0;
        for (int j = 0; j < k; j++)
            current_sum = current_sum + arr[i + j];

        // Update result if required.
        max_sum = max(current_sum, max_sum);
    }

    return max_sum;
}

// Driver code
int main()
{
    int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
    int k = 4;
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("%d", maxSum(arr, n, k));
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

Java

// Java code O(n*k) solution for finding maximum sum of
// a subarray of size k
class GFG {
    // Returns maximum sum in
    // a subarray of size k.
    static int maxSum(int arr[], int n, int k)
    {
        // Initialize result
        int max_sum = Integer.MIN_VALUE;

        // Consider all blocks starting with i.
        for (int i = 0; i < n - k + 1; i++) {
            int current_sum = 0;
            for (int j = 0; j < k; j++)
                current_sum = current_sum + arr[i + j];

            // Update result if required.
            max_sum = Math.max(current_sum, max_sum);
        }

        return max_sum;
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
        int k = 4;
        int n = arr.length;
        System.out.println(maxSum(arr, n, k));
    }
}

Python

import sys

# O(n * k) solution for finding
# maximum sum of a subarray of size k


# Returns maximum sum in a
# subarray of size k.


def maxSum(arr, n, k):

    # Initialize result
    max_sum = -sys.maxsize

    # Consider all blocks
    # starting with i.
    for i in range(n - k + 1):
        current_sum = 0
        for j in range(k):
            current_sum = current_sum + arr[i + j]

        # Update result if required.
        max_sum = max(current_sum, max_sum)

    return max_sum


# Driver code
arr = [1, 4, 2, 10, 2,
       3, 1, 0, 20]
k = 4
n = len(arr)
print(maxSum(arr, n, k))

// C# code here O(n*k) solution for
// finding maximum sum of a subarray
// of size k
using System;

class GFG {

    // Returns maximum sum in a
    // subarray of size k.
    static int maxSum(int[] arr, int n, int k)
    {
        // Initialize result
        int max_sum = int.MinValue;

        // Consider all blocks starting
        // with i.
        for (int i = 0; i < n - k + 1; i++) {
            int current_sum = 0;
            for (int j = 0; j < k; j++)
                current_sum = current_sum + arr[i + j];

            // Update result if required.
            max_sum = Math.Max(current_sum, max_sum);
        }

        return max_sum;
    }

    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
        int k = 4;
        int n = arr.Length;
        Console.WriteLine(maxSum(arr, n, k));
    }
}

JavaScript

// Function to find the maximum sum of a subarray of size k
function maxSum(arr, n, k) {
    
    // Initialize result
    let max_sum = Number.MIN_SAFE_INTEGER;

    // Consider all blocks starting with i
    for (let i = 0; i < n - k + 1; i++) {
        let current_sum = 0;
        for (let j = 0; j < k; j++) {
            current_sum += arr[i + j];
        }

        // Update result if required
        max_sum = Math.max(current_sum, max_sum);
    }

    return max_sum;
}

// Driver code
const arr = [1, 4, 2, 10, 2, 3, 1, 0, 20];
const k = 4;
const n = arr.length;
console.log(maxSum(arr, n, k));

PHP

<?php
    // code
?>
<?php
// O(n*k) solution for finding maximum sum of
// a subarray of size k

// Returns maximum sum in a subarray of size k.
function maxSum($arr, $n, $k)
{
    
    // Initialize result
    $max_sum = PHP_INT_MIN ;

    // Consider all blocks 
    // starting with i.
    for ( $i = 0; $i < $n - $k + 1; $i++)
    {
        $current_sum = 0;
        for ( $j = 0; $j < $k; $j++)
            $current_sum = $current_sum + 
                   gold         $arr[$i + $j];

        // Update result if required.
        $max_sum = max($current_sum, $max_sum );
    }

    return $max_sum;
}

    // Driver code
    $arr = array(1, 4, 2, 10, 2, 3, 1, 0, 20);
    $k = 4;
    $n = count($arr);
    echo maxSum($arr, $n, $k);
?>

Output

Using the Sliding Window Technique - O(n) Time and O(1) Space

We compute the sum of the first k elements out of n terms using a linear loop and store the sum in variable window_sum.
Then we will traverse linearly over the array till it reaches the end and simultaneously keep track of the maximum sum.
To get the current sum of a block of k elements just subtract the first element from the previous block and add the last element of the current block.

The below representation will make it clear how the window slides over the array.

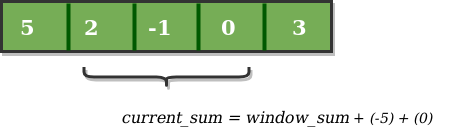
Consider an array arr[] = {5, 2, -1, 0, 3} and value of k = 3 and n = 5
This is the initial phase where we have calculated the initial window sum starting from index 0 . At this stage the window sum is 6. Now, we set the maximum_sum as current_window i.e 6.

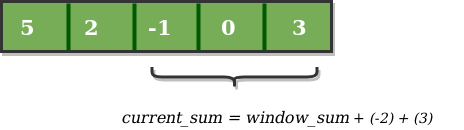
Now, we slide our window by a unit index. Therefore, now it discards 5 from the window and adds 0 to the window. Hence, we will get our new window sum by subtracting 5 and then adding 0 to it. So, our window sum now becomes 1. Now, we will compare this window sum with the maximum_sum. As it is smaller, we won't change the maximum_sum.

Similarly, now once again we slide our window by a unit index and obtain the new window sum to be 2. Again we check if this current window sum is greater than the maximum_sum till now. Once, again it is smaller so we don't change the maximum_sum.
Therefore, for the above array our maximum_sum is 6.

Below is the code for above approach:

C++

#include <iostream>
#include <vector>
using namespace std;

// Returns maximum sum in a subarray of size k.
int maxSum(vector<int>& arr, int k)
{
    int n = arr.size();

    // n must be greater
    if (n <= k) {
        cout << "Invalid";
        return -1;
    }

    // Compute sum of first window of size k
    int max_sum = 0;
    for (int i = 0; i < k; i++)
        max_sum += arr[i];

    // Compute sums of remaining windows by
    // removing first element of previous
    // window and adding last element of
    // current window.
    int window_sum = max_sum;
    for (int i = k; i < n; i++) {
        window_sum += arr[i] - arr[i - k];
        max_sum = max(max_sum, window_sum);
    }

    return max_sum;
}

// Driver code
int main()
{
    vector<int> arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
    int k = 4;
    cout << maxSum(arr, k);
    return 0;
}

Java

// Java code for
// O(n) solution for finding
// maximum sum of a subarray
// of size k
class GFG {

    // Returns maximum sum in
    // a subarray of size k.
    static int maxSum(int arr[], int n, int k)
    {
        // n must be greater
        if (n <= k) {
            System.out.println("Invalid");
            return -1;
        }

        // Compute sum of first window of size k
        int max_sum = 0;
        for (int i = 0; i < k; i++)
            max_sum += arr[i];

        // Compute sums of remaining windows by
        // removing first element of previous
        // window and adding last element of
        // current window.
        int window_sum = max_sum;
        for (int i = k; i < n; i++) {
            window_sum += arr[i] - arr[i - k];
            max_sum = Math.max(max_sum, window_sum);
        }

        return max_sum;
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
        int k = 4;
        int n = arr.length;
        System.out.println(maxSum(arr, n, k));
    }
}

Python

# O(n) solution for finding
# maximum sum of a subarray of size k


def maxSum(arr, k):
    
    # length of the array
    n = len(arr)

    # n must be greater than k
    if n <= k:
        print("Invalid")
        return -1

    # Compute sum of first window of size k
    window_sum = sum(arr[:k])

    # first sum available
    max_sum = window_sum

    # Compute the sums of remaining windows by
    # removing first element of previous
    # window and adding last element of
    # the current window.
    for i in range(n - k):
        window_sum = window_sum - arr[i] + arr[i + k]
        max_sum = max(window_sum, max_sum)

    return max_sum


# Driver code
arr = [1, 4, 2, 10, 2, 3, 1, 0, 20]
k = 4
print(maxSum(arr, k))

// C# code for O(n) solution for finding
// maximum sum of a subarray of size k
using System;

class GFG {

    // Returns maximum sum in
    // a subarray of size k.
    static int maxSum(int[] arr, int n, int k)
    {

        // n must be greater
        if (n <= k) {
            Console.WriteLine("Invalid");
            return -1;
        }

        // Compute sum of first window of size k
        int max_sum = 0;
        for (int i = 0; i < k; i++)
            max_sum += arr[i];

        // Compute sums of remaining windows by
        // removing first element of previous
        // window and adding last element of
        // current window.
        int window_sum = max_sum;
        for (int i = k; i < n; i++) {
            window_sum += arr[i] - arr[i - k];
            max_sum = Math.Max(max_sum, window_sum);
        }

        return max_sum;
    }

    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
        int k = 4;
        int n = arr.Length;
        Console.WriteLine(maxSum(arr, n, k));
    }
}

// This code is contributed by anuj_67.

JavaScript

function maxSum(arr, k) {
    const n = arr.length;
    if (n < k) {
        console.log("Invalid");
        return -1;
    }

    // Compute sum of first window of size k
    let windowSum = 0;
    for (let i = 0; i < k; i++) {
        windowSum += arr[i];
    }

    let maxSum = windowSum;

    // Slide the window from start to end of the array
    for (let i = k; i < n; i++) {
        windowSum += arr[i] - arr[i - k];
        maxSum = Math.max(maxSum, windowSum);
    }

    return maxSum;
}

// Example usage
const arr = [1, 4, 2, 10, 2, 3, 1, 0, 20];
const k = 4;
console.log(maxSum(arr, k)); // Output: 24

PHP

<?php
// O(n) solution for finding maximum sum of
// a subarray of size k

// Returns maximum sum in a 
// subarray of size k.
function maxSum( $arr, $n, $k)
{
    // n must be greater
    if ($n <= $k)
    {
        echo "Invalid";
        return -1;
    }

    // Compute sum of first
    // window of size k
    $max_sum = 0;
    for($i = 0; $i < $k; $i++)
    $max_sum += $arr[$i];

    // Compute sums of remaining windows by
    // removing first element of previous
    // window and adding last element of
    // current window.
    $window_sum = $max_sum;
    for ($i = $k; $i < $n; $i++)
    {
        $window_sum += $arr[$i] - $arr[$i - $k];
        $max_sum = max($max_sum, $window_sum);
    }

    return $max_sum;
}

    // Driver code
    $arr = array(1, 4, 2, 10, 2, 3, 1, 0, 20);
    $k = 4;
    $n = count($arr);
    echo maxSum($arr, $n, $k);

// This code is contributed by anuj_67
?>

Output

How to use Sliding Window Technique?

There are basically two types of sliding window:

1. Fixed Size Sliding Window:

The general steps to solve these questions by following below steps:

Find the size of the window required, say K.
Compute the result for 1st window, i.e. include the first K elements of the data structure.
Then use a loop to slide the window by 1 and keep computing the result window by window.

2. Variable Size Sliding Window:

The general steps to solve these questions by following below steps:

In this type of sliding window problem, we increase our right pointer one by one till our condition is true.
At any step if our condition does not match, we shrink the size of our window by increasing left pointer.
Again, when our condition satisfies, we start increasing the right pointer and follow step 1.
We follow these steps until we reach to the end of the array.

How to Identify Sliding Window Problems?

These problems generally require Finding Maximum/Minimum Subarray, Substrings which satisfy some specific condition.
The size of the subarray or substring ‘k’ will be given in some of the problems.
These problems can easily be solved in O(n²) time complexity using nested loops, using sliding window we can solve these in O(n) Time Complexity.
Required Time Complexity: O(n) or O(n log n)
Constraints: n <= 10⁶

Sliding Window Technique

Example Problem - Maximum Sum of a Subarray with K Elements

Naive Approach - O(n k) Time and O(1) Space

Using the Sliding Window Technique - O(n) Time and O(1) Space

How to use Sliding Window Technique?

How to Identify Sliding Window Problems?

More Example Problems

Similar Reads

Sliding Window Technique

Example Problem - Maximum Sum of a Subarray with K Elements

Naive Approach - O(n k) Time and O(1) Space

Using the Sliding Window Technique - O(n) Time and O(1) Space

How to use Sliding Window Technique?

How to Identify Sliding Window Problems?

More Example Problems

Similar Reads

Basics & Prerequisites

Data Structures

Algorithms

Advanced

Interview Preparation

Practice Problem

Thank You!

What kind of Experience do you want to share?