Eulerian path and circuit for undirected graph

Given an undirected connected graph with v nodes, and e edges, with adjacency list adj. We need to write a function that returns 2 if the graph contains an eulerian circuit or cycle, else if the graph contains an eulerian path, returns 1, otherwise, returns 0.
A graph is said to be Eulerian if it contains an Eulerian Cycle, a cycle that visits every edge exactly once and starts and ends at the same vertex.
If a graph contains an Eulerian Path, a path that visits every edge exactly once but starts and ends at different vertices, it is called Semi-Eulerian.
Examples:
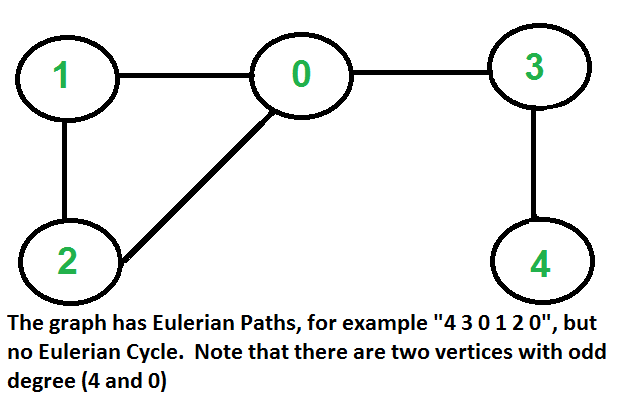
Input:
Output: 1
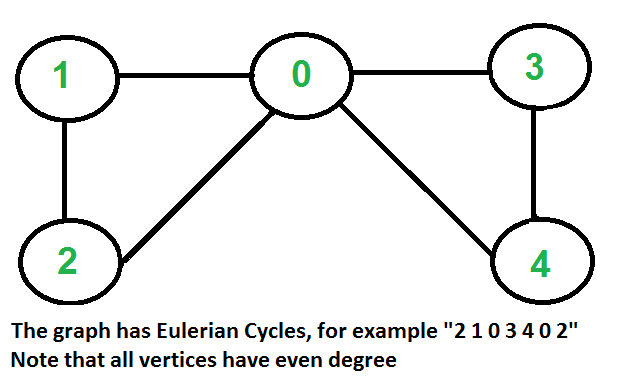
Input:
Output: 2
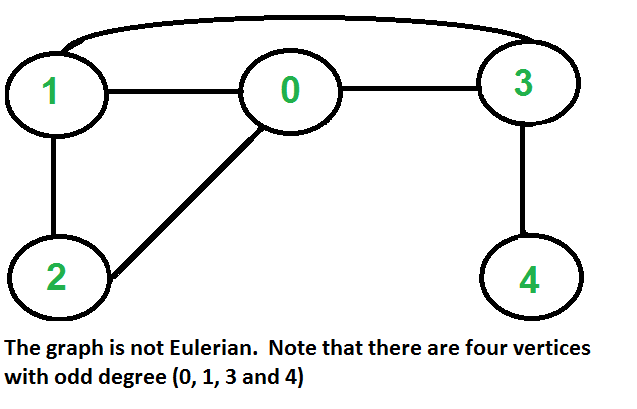
Input:
Output: 0
The problem can be framed as follows: "Is it possible to draw a graph without lifting your pencil from the paper and without retracing any edge?"
At first glance, this may seem similar to the Hamiltonian Path problem, which is NP-complete for general graphs. However, determining whether a graph has an Eulerian Path or Cycle is much more efficient: It can be solved in O(v + e) time.
Approach:
The idea is to use some key properties of undirected graphs that help determine whether they are Eulerian (i.e., contain an Eulerian Path or Cycle) or not.
Eulerian Cycle
A graph has an Eulerian Cycle if and only if the below two conditions are true
- All vertices with non-zero degree are part of a single connected component. (We ignore isolated vertices— those with zero degree — as they do not affect the cycle.)
- Every vertex in the graph has an even degree.
Eulerian Path
A graph has an Eulerian Path if and only if the below two conditions are true
- All vertices with non-zero degree must belong to the same connected component. (Same as Eulerian Cycle)
- Exactly Zero or Two Vertices with Odd Degree:
- If zero vertices have odd degree → Eulerian Cycle exists (which is also a path).
- If two vertices have odd degree → Eulerian Path exists (but not a cycle).
- If one vertex has odd degree → Not possible in an undirected graph. (Because the sum of all degrees in an undirected graph is always even.)
Note: A graph with no edges is trivially Eulerian. There are no edges to traverse, so by definition, it satisfies both Eulerian Path and Cycle conditions.
How Does This Work?
- In an Eulerian Path, whenever we enter a vertex (except start and end), we must also leave it. So all intermediate vertices must have even degree.
- In an Eulerian Cycle, since we start and end at the same vertex, every vertex must have even degree. This ensures that every entry into a vertex can be paired with an exit.
Steps to implement the above idea:
- Create an adjacency list to represent the graph and initialize a visited array for DFS traversal.
- Perform DFS starting from the first vertex having non-zero degree to check graph connectivity.
- After DFS, ensure all non-zero degree vertices were visited to confirm the graph is connected.
- Count the number of vertices with odd degree to classify the graph as Eulerian or not.
- If all degrees are even, the graph has an Eulerian Circuit; if exactly two are odd, it's a Path.
- If more than two vertices have odd degree or graph isn't connected, it's not Eulerian.
- Return 2 for Circuit, 1 for Path, and 0 when graph fails Eulerian conditions.
// C++ program to check whether a graph is
// Eulerian Path, Eulerian Circuit, or neither
#include <bits/stdc++.h>
using namespace std;
// DFS to check connectivity, excluding zero-degree vertices
void dfs(int node, vector<int> adj[], vector<bool> &visited) {
visited[node] = true;
for (int neighbor : adj[node]) {
if (!visited[neighbor]) {
dfs(neighbor, adj, visited);
}
}
}
// Function to check Eulerian Path or Circuit
int isEulerCircuit(int v, vector<int> adj[]) {
vector<bool> visited(v, false);
// Find first vertex with non-zero degree
int start = -1;
for (int i = 0; i < v; i++) {
if (adj[i].size() > 0) {
start = i;
break;
}
}
// No edges: graph is trivially Eulerian
if (start == -1) {
return 2;
}
// DFS from the first non-zero degree vertex
dfs(start, adj, visited);
// Check if all non-zero degree vertices are connected
for (int i = 0; i < v; i++) {
if (adj[i].size() > 0 && !visited[i]) {
return 0; // Not connected
}
}
// Count vertices with odd degree
int odd = 0;
for (int i = 0; i < v; i++) {
if (adj[i].size() % 2 != 0) {
odd++;
}
}
// Apply Eulerian rules
if (odd == 0) {
return 2;
} else if (odd == 2) {
return 1;
} else {
return 0;
}
}
// Driver code
int main() {
int v = 5;
vector<int> adj[5] = {{1, 2, 3}, {0, 2},
{1, 0}, {0, 4}, {3}};
cout << isEulerCircuit(v, adj);
return 0;
}
// Java program to check whether a graph is
// Eulerian Path, Eulerian Circuit, or neither
import java.util.*;
class GfG {
// DFS to check connectivity, excluding zero-degree vertices
static void dfs(int node, List<Integer>[] adj, boolean[] visited) {
visited[node] = true;
for (int neighbor : adj[node]) {
if (!visited[neighbor]) {
dfs(neighbor, adj, visited);
}
}
}
// Function to check Eulerian Path or Circuit
static int isEulerCircuit(int v, List<Integer>[] adj) {
boolean[] visited = new boolean[v];
// Find first vertex with non-zero degree
int start = -1;
for (int i = 0; i < v; i++) {
if (adj[i].size() > 0) {
start = i;
break;
}
}
// No edges: graph is trivially Eulerian
if (start == -1) {
return 2;
}
// DFS from the first non-zero degree vertex
dfs(start, adj, visited);
// Check if all non-zero degree vertices are connected
for (int i = 0; i < v; i++) {
if (adj[i].size() > 0 && !visited[i]) {
return 0; // Not connected
}
}
// Count vertices with odd degree
int odd = 0;
for (int i = 0; i < v; i++) {
if (adj[i].size() % 2 != 0) {
odd++;
}
}
// Apply Eulerian rules
if (odd == 0) {
return 2;
} else if (odd == 2) {
return 1;
} else {
return 0;
}
}
public static void main(String[] args) {
int v = 5;
List<Integer>[] adj = new ArrayList[v];
for (int i = 0; i < v; i++) {
adj[i] = new ArrayList<>();
}
adj[0].addAll(Arrays.asList(1, 2, 3));
adj[1].addAll(Arrays.asList(0, 2));
adj[2].addAll(Arrays.asList(1, 0));
adj[3].addAll(Arrays.asList(0, 4));
adj[4].addAll(Arrays.asList(3));
System.out.println(isEulerCircuit(v, adj));
}
}
# Python program to check whether a graph is
# Eulerian Path, Eulerian Circuit, or neither
# DFS to check connectivity, excluding zero-degree vertices
def dfs(node, adj, visited):
visited[node] = True
for neighbor in adj[node]:
if not visited[neighbor]:
dfs(neighbor, adj, visited)
# Function to check Eulerian Path or Circuit
def isEulerCircuit(v, adj):
visited = [False] * v
# Find first vertex with non-zero degree
start = -1
for i in range(v):
if len(adj[i]) > 0:
start = i
break
# No edges: graph is trivially Eulerian
if start == -1:
return 2
# DFS from the first non-zero degree vertex
dfs(start, adj, visited)
# Check if all non-zero degree vertices are connected
for i in range(v):
if len(adj[i]) > 0 and not visited[i]:
return 0 # Not connected
# Count vertices with odd degree
odd = 0
for i in range(v):
if len(adj[i]) % 2 != 0:
odd += 1
# Apply Eulerian rules
if odd == 0:
return 2
elif odd == 2:
return 1
else:
return 0
if __name__ == "__main__":
v = 5
adj = [
[1, 2, 3],
[0, 2],
[1, 0],
[0, 4],
[3]
]
print(isEulerCircuit(v, adj))
// C# program to check whether a graph is
// Eulerian Path, Eulerian Circuit, or neither
using System;
using System.Collections.Generic;
class GfG {
// DFS to check connectivity, excluding zero-degree vertices
static void dfs(int node, List<int>[] adj, bool[] visited) {
visited[node] = true;
foreach (int neighbor in adj[node]) {
if (!visited[neighbor]) {
dfs(neighbor, adj, visited);
}
}
}
// Function to check Eulerian Path or Circuit
static int isEulerCircuit(int v, List<int>[] adj) {
bool[] visited = new bool[v];
// Find first vertex with non-zero degree
int start = -1;
for (int i = 0; i < v; i++) {
if (adj[i].Count > 0) {
start = i;
break;
}
}
// No edges: graph is trivially Eulerian
if (start == -1) {
return 2;
}
// DFS from the first non-zero degree vertex
dfs(start, adj, visited);
// Check if all non-zero degree vertices are connected
for (int i = 0; i < v; i++) {
if (adj[i].Count > 0 && !visited[i]) {
return 0; // Not connected
}
}
// Count vertices with odd degree
int odd = 0;
for (int i = 0; i < v; i++) {
if (adj[i].Count % 2 != 0) {
odd++;
}
}
// Apply Eulerian rules
if (odd == 0) {
return 2;
} else if (odd == 2) {
return 1;
} else {
return 0;
}
}
static void Main() {
int v = 5;
List<int>[] adj = new List<int>[v];
for (int i = 0; i < v; i++) {
adj[i] = new List<int>();
}
adj[0].AddRange(new int[] {1, 2, 3});
adj[1].AddRange(new int[] {0, 2});
adj[2].AddRange(new int[] {1, 0});
adj[3].AddRange(new int[] {0, 4});
adj[4].AddRange(new int[] {3});
Console.WriteLine(isEulerCircuit(v, adj));
}
}
// JavaScript program to check whether a graph is
// Eulerian Path, Eulerian Circuit, or neither
// DFS to check connectivity, excluding zero-degree vertices
function dfs(node, adj, visited) {
visited[node] = true;
for (let neighbor of adj[node]) {
if (!visited[neighbor]) {
dfs(neighbor, adj, visited);
}
}
}
// Function to check Eulerian Path or Circuit
function isEulerCircuit(v, adj) {
let visited = new Array(v).fill(false);
// Find first vertex with non-zero degree
let start = -1;
for (let i = 0; i < v; i++) {
if (adj[i].length > 0) {
start = i;
break;
}
}
// No edges: graph is trivially Eulerian
if (start === -1) {
return 2;
}
// DFS from the first non-zero degree vertex
dfs(start, adj, visited);
// Check if all non-zero degree vertices are connected
for (let i = 0; i < v; i++) {
if (adj[i].length > 0 && !visited[i]) {
return 0; // Not connected
}
}
// Count vertices with odd degree
let odd = 0;
for (let i = 0; i < v; i++) {
if (adj[i].length % 2 !== 0) {
odd++;
}
}
// Apply Eulerian rules
if (odd === 0) {
return 2;
} else if (odd === 2) {
return 1;
} else {
return 0;
}
}
// Driver Code
let v = 5;
let adj = [
[1, 2, 3],
[0, 2],
[1, 0],
[0, 4],
[3]
];
console.log(isEulerCircuit(v, adj));
Output
1
Time Complexity: O(v + e), DFS traverses all vertices and edges to check connectivity and degree.
Space Complexity: O(v + e), Space used for visited array and adjacency list to represent graph.