Ford-Fulkerson Algorithm for Maximum Flow Problem
The Ford-Fulkerson algorithm is a widely used algorithm to solve the maximum flow problem in a flow network. The maximum flow problem involves determining the maximum amount of flow that can be sent from a source vertex to a sink vertex in a directed weighted graph, subject to capacity constraints on the edges.
The algorithm works by iteratively finding an augmenting path, which is a path from the source to the sink in the residual graph, i.e., the graph obtained by subtracting the current flow from the capacity of each edge. The algorithm then increases the flow along this path by the maximum possible amount, which is the minimum capacity of the edges along the path.
Problem:
Given a graph which represents a flow network where every edge has a capacity. Also, given two vertices source 's' and sink 't' in the graph, find the maximum possible flow from s to t with the following constraints:
- Flow on an edge doesn't exceed the given capacity of the edge.
- Incoming flow is equal to outgoing flow for every vertex except s and t.
For example, consider the following graph from the CLRS book.
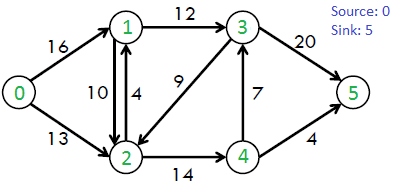
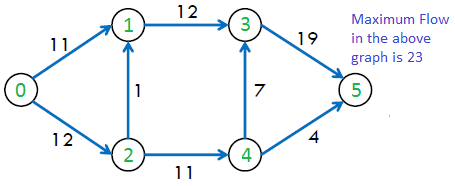
The maximum possible flow in the above graph is 23.
Prerequisite : Max Flow Problem Introduction
Ford-Fulkerson Algorithm
The following is simple idea of Ford-Fulkerson algorithm:
- Start with initial flow as 0.
- While there exists an augmenting path from the source to the sink:
- Find an augmenting path using any path-finding algorithm, such as breadth-first search or depth-first search.
- Determine the amount of flow that can be sent along the augmenting path, which is the minimum residual capacity along the edges of the path.
- Increase the flow along the augmenting path by the determined amount.
- Return the maximum flow.
Time Complexity: Time complexity of the above algorithm is O(max_flow * E). We run a loop while there is an augmenting path. In worst case, we may add 1 unit flow in every iteration. Therefore the time complexity becomes O(max_flow * E).
How to implement the above simple algorithm?
Let us first define the concept of Residual Graph which is needed for understanding the implementation.
Residual Graph of a flow network is a graph which indicates additional possible flow. If there is a path from source to sink in residual graph, then it is possible to add flow. Every edge of a residual graph has a value called residual capacity which is equal to original capacity of the edge minus current flow. Residual capacity is basically the current capacity of the edge.
Let us now talk about implementation details. Residual capacity is 0 if there is no edge between two vertices of residual graph. We can initialize the residual graph as original graph as there is no initial flow and initially residual capacity is equal to original capacity. To find an augmenting path, we can either do a BFS or DFS of the residual graph. We have used BFS in below implementation. Using BFS, we can find out if there is a path from source to sink. BFS also builds parent[] array. Using the parent[] array, we traverse through the found path and find possible flow through this path by finding minimum residual capacity along the path. We later add the found path flow to overall flow.
The important thing is, we need to update residual capacities in the residual graph. We subtract path flow from all edges along the path and we add path flow along the reverse edges We need to add path flow along reverse edges because may later need to send flow in reverse direction (See following link for example).
https://www.geeksforgeeks.org/dsa/max-flow-problem-introduction/
Below is the implementation of Ford-Fulkerson algorithm. To keep things simple, graph is represented as a 2D matrix.
// C++ program for implementation of Ford Fulkerson
// algorithm
#include <iostream>
#include <limits.h>
#include <queue>
#include <string.h>
using namespace std;
// Number of vertices in given graph
#define V 6
/* Returns true if there is a path from source 's' to sink
't' in residual graph. Also fills parent[] to store the
path */
bool bfs(int rGraph[V][V], int s, int t, int parent[])
{
// Create a visited array and mark all vertices as not
// visited
bool visited[V];
memset(visited, 0, sizeof(visited));
// Create a queue, enqueue source vertex and mark source
// vertex as visited
queue<int> q;
q.push(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v = 0; v < V; v++) {
if (visited[v] == false && rGraph[u][v] > 0) {
// If we find a connection to the sink node,
// then there is no point in BFS anymore We
// just have to set its parent and can return
// true
if (v == t) {
parent[v] = u;
return true;
}
q.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting from source, so
// return false
return false;
}
// Returns the maximum flow from s to t in the given graph
int fordFulkerson(int graph[V][V], int s, int t)
{
int u, v;
// Create a residual graph and fill the residual graph
// with given capacities in the original graph as
// residual capacities in residual graph
int rGraph[V]
[V]; // Residual graph where rGraph[i][j]
// indicates residual capacity of edge
// from i to j (if there is an edge. If
// rGraph[i][j] is 0, then there is not)
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
int parent[V]; // This array is filled by BFS and to
// store path
int max_flow = 0; // There is no flow initially
// Augment the flow while there is path from source to
// sink
while (bfs(rGraph, s, t, parent)) {
// Find minimum residual capacity of the edges along
// the path filled by BFS. Or we can say find the
// maximum flow through the path found.
int path_flow = INT_MAX;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow = min(path_flow, rGraph[u][v]);
}
// update residual capacities of the edges and
// reverse edges along the path
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver program to test above functions
int main()
{
// Let us create a graph shown in the above example
int graph[V][V]
= { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } };
cout << "The maximum possible flow is "
<< fordFulkerson(graph, 0, 5);
return 0;
}
// Java program for implementation of Ford Fulkerson
// algorithm
import java.io.*;
import java.lang.*;
import java.util.*;
import java.util.LinkedList;
class MaxFlow {
static final int V = 6; // Number of vertices in graph
/* Returns true if there is a path from source 's' to
sink 't' in residual graph. Also fills parent[] to
store the path */
boolean bfs(int rGraph[][], int s, int t, int parent[])
{
// Create a visited array and mark all vertices as
// not visited
boolean visited[] = new boolean[V];
for (int i = 0; i < V; ++i)
visited[i] = false;
// Create a queue, enqueue source vertex and mark
// source vertex as visited
LinkedList<Integer> queue
= new LinkedList<Integer>();
queue.add(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (queue.size() != 0) {
int u = queue.poll();
for (int v = 0; v < V; v++) {
if (visited[v] == false
&& rGraph[u][v] > 0) {
// If we find a connection to the sink
// node, then there is no point in BFS
// anymore We just have to set its parent
// and can return true
if (v == t) {
parent[v] = u;
return true;
}
queue.add(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting from source,
// so return false
return false;
}
// Returns the maximum flow from s to t in the given
// graph
int fordFulkerson(int graph[][], int s, int t)
{
int u, v;
// Create a residual graph and fill the residual
// graph with given capacities in the original graph
// as residual capacities in residual graph
// Residual graph where rGraph[i][j] indicates
// residual capacity of edge from i to j (if there
// is an edge. If rGraph[i][j] is 0, then there is
// not)
int rGraph[][] = new int[V][V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
// This array is filled by BFS and to store path
int parent[] = new int[V];
int max_flow = 0; // There is no flow initially
// Augment the flow while there is path from source
// to sink
while (bfs(rGraph, s, t, parent)) {
// Find minimum residual capacity of the edges
// along the path filled by BFS. Or we can say
// find the maximum flow through the path found.
int path_flow = Integer.MAX_VALUE;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow
= Math.min(path_flow, rGraph[u][v]);
}
// update residual capacities of the edges and
// reverse edges along the path
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver program to test above functions
public static void main(String[] args)
throws java.lang.Exception
{
// Let us create a graph shown in the above example
int graph[][] = new int[][] {
{ 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 }
};
MaxFlow m = new MaxFlow();
System.out.println("The maximum possible flow is "
+ m.fordFulkerson(graph, 0, 5));
}
}
# Python program for implementation
# of Ford Fulkerson algorithm
from collections import defaultdict
# This class represents a directed graph
# using adjacency matrix representation
class Graph:
def __init__(self, graph):
self.graph = graph # residual graph
self. ROW = len(graph)
# self.COL = len(gr[0])
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
def BFS(self, s, t, parent):
# Mark all the vertices as not visited
visited = [False]*(self.ROW)
# Create a queue for BFS
queue = []
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
# Dequeue a vertex from queue and print it
u = queue.pop(0)
# Get all adjacent vertices of the dequeued vertex u
# If a adjacent has not been visited, then mark it
# visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
# If we find a connection to the sink node,
# then there is no point in BFS anymore
# We just have to set its parent and can return true
queue.append(ind)
visited[ind] = True
parent[ind] = u
if ind == t:
return True
# We didn't reach sink in BFS starting
# from source, so return false
return False
# Returns the maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1]*(self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent) :
# Find minimum residual capacity of the edges along the
# path filled by BFS. Or we can say find the maximum flow
# through the path found.
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges
# along the path
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
# Create a graph given in the above diagram
graph = [[0, 16, 13, 0, 0, 0],
[0, 0, 10, 12, 0, 0],
[0, 4, 0, 0, 14, 0],
[0, 0, 9, 0, 0, 20],
[0, 0, 0, 7, 0, 4],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0; sink = 5
print ("The maximum possible flow is %d " % g.FordFulkerson(source, sink))
# This code is contributed by Neelam Yadav
// C# program for implementation
// of Ford Fulkerson algorithm
using System;
using System.Collections.Generic;
public class MaxFlow {
static readonly int V = 6; // Number of vertices in
// graph
/* Returns true if there is a path
from source 's' to sink 't' in residual
graph. Also fills parent[] to store the
path */
bool bfs(int[, ] rGraph, int s, int t, int[] parent)
{
// Create a visited array and mark
// all vertices as not visited
bool[] visited = new bool[V];
for (int i = 0; i < V; ++i)
visited[i] = false;
// Create a queue, enqueue source vertex and mark
// source vertex as visited
List<int> queue = new List<int>();
queue.Add(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (queue.Count != 0) {
int u = queue[0];
queue.RemoveAt(0);
for (int v = 0; v < V; v++) {
if (visited[v] == false
&& rGraph[u, v] > 0) {
// If we find a connection to the sink
// node, then there is no point in BFS
// anymore We just have to set its parent
// and can return true
if (v == t) {
parent[v] = u;
return true;
}
queue.Add(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting from source,
// so return false
return false;
}
// Returns the maximum flow
// from s to t in the given graph
int fordFulkerson(int[, ] graph, int s, int t)
{
int u, v;
// Create a residual graph and fill
// the residual graph with given
// capacities in the original graph as
// residual capacities in residual graph
// Residual graph where rGraph[i,j]
// indicates residual capacity of
// edge from i to j (if there is an
// edge. If rGraph[i,j] is 0, then
// there is not)
int[, ] rGraph = new int[V, V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u, v] = graph[u, v];
// This array is filled by BFS and to store path
int[] parent = new int[V];
int max_flow = 0; // There is no flow initially
// Augment the flow while there is path from source
// to sink
while (bfs(rGraph, s, t, parent)) {
// Find minimum residual capacity of the edges
// along the path filled by BFS. Or we can say
// find the maximum flow through the path found.
int path_flow = int.MaxValue;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow
= Math.Min(path_flow, rGraph[u, v]);
}
// update residual capacities of the edges and
// reverse edges along the path
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u, v] -= path_flow;
rGraph[v, u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver code
public static void Main()
{
// Let us create a graph shown in the above example
int[, ] graph = new int[, ] {
{ 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 }
};
MaxFlow m = new MaxFlow();
Console.WriteLine("The maximum possible flow is "
+ m.fordFulkerson(graph, 0, 5));
}
}
/* This code contributed by PrinciRaj1992 */
<script>
// Javascript program for implementation of Ford
// Fulkerson algorithm
// Number of vertices in graph
let V = 6;
// Returns true if there is a path from source
// 's' to sink 't' in residual graph. Also
// fills parent[] to store the path
function bfs(rGraph, s, t, parent)
{
// Create a visited array and mark all
// vertices as not visited
let visited = new Array(V);
for(let i = 0; i < V; ++i)
visited[i] = false;
// Create a queue, enqueue source vertex
// and mark source vertex as visited
let queue = [];
queue.push(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (queue.length != 0)
{
let u = queue.shift();
for(let v = 0; v < V; v++)
{
if (visited[v] == false &&
rGraph[u][v] > 0)
{
// If we find a connection to the sink
// node, then there is no point in BFS
// anymore We just have to set its parent
// and can return true
if (v == t)
{
parent[v] = u;
return true;
}
queue.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting
// from source, so return false
return false;
}
// Returns the maximum flow from s to t in
// the given graph
function fordFulkerson(graph, s, t)
{
let u, v;
// Create a residual graph and fill the
// residual graph with given capacities
// in the original graph as residual
// capacities in residual graph
// Residual graph where rGraph[i][j]
// indicates residual capacity of edge
// from i to j (if there is an edge.
// If rGraph[i][j] is 0, then there is
// not)
let rGraph = new Array(V);
for(u = 0; u < V; u++)
{
rGraph[u] = new Array(V);
for(v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
}
// This array is filled by BFS and to store path
let parent = new Array(V);
// There is no flow initially
let max_flow = 0;
// Augment the flow while there
// is path from source to sink
while (bfs(rGraph, s, t, parent))
{
// Find minimum residual capacity of the edges
// along the path filled by BFS. Or we can say
// find the maximum flow through the path found.
let path_flow = Number.MAX_VALUE;
for(v = t; v != s; v = parent[v])
{
u = parent[v];
path_flow = Math.min(path_flow,
rGraph[u][v]);
}
// Update residual capacities of the edges and
// reverse edges along the path
for(v = t; v != s; v = parent[v])
{
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver code
// Let us create a graph shown in the above example
let graph = [ [ 0, 16, 13, 0, 0, 0 ],
[ 0, 0, 10, 12, 0, 0 ],
[ 0, 4, 0, 0, 14, 0 ],
[ 0, 0, 9, 0, 0, 20 ],
[ 0, 0, 0, 7, 0, 4 ],
[ 0, 0, 0, 0, 0, 0 ] ];
document.write("The maximum possible flow is " +
fordFulkerson(graph, 0, 5));
// This code is contributed by avanitrachhadiya2155
</script>
Output
The maximum possible flow is 23
Time Complexity : O(|V| * E^2) ,where E is the number of edges and V is the number of vertices.
Space Complexity :O(V) , as we created queue.
The above implementation of Ford Fulkerson Algorithm is called Edmonds-Karp Algorithm. The idea of Edmonds-Karp is to use BFS in Ford Fulkerson implementation as BFS always picks a path with minimum number of edges. When BFS is used, the worst case time complexity can be reduced to O(VE2). The above implementation uses adjacency matrix representation though where BFS takes O(V2) time, the time complexity of the above implementation is O(EV3) (Refer CLRS book for proof of time complexity)
This is an important problem as it arises in many practical situations. Examples include, maximizing the transportation with given traffic limits, maximizing packet flow in computer networks.
Dinc's Algorithm for Max-Flow.
Exercise:
Modify the above implementation so that it that runs in O(VE2) time.
