Heap Data Structure
Last Updated :
23 Jul, 2025
Improve
A Heap is a complete binary tree data structure that satisfies the heap property: for every node, the value of its children is greater than or equal to its own value. Heaps are usually used to implement priority queues, where the smallest (or largest) element is always at the root of the tree.
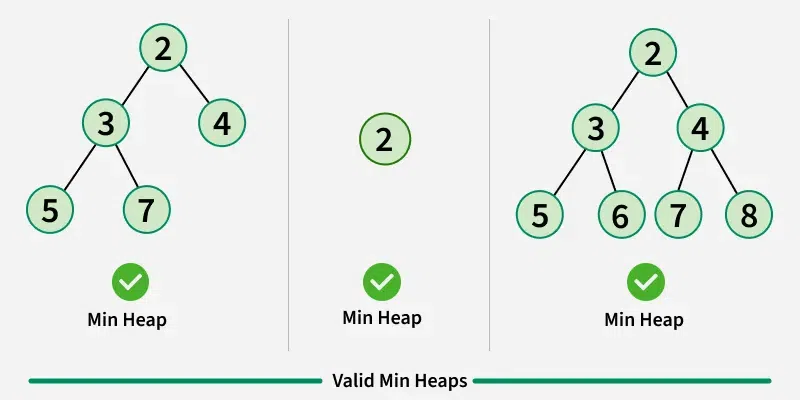







Basics
Library Implementations
- Heap in C++ STL
- priority_queue in C++
- PriorityQueue in Java
- PriorityQueue in C#
- heapq in Python
- Heap in JavaScript
Easy Problems
- Check if an array is Heap?
- K’th Smallest & K'th Largest
- Heap Sort
- Heap Sort for Decreasing Order
- Height of a Heap with N Nodes
Medium Problems
- Nearly Sorted Array
- K Largest Elements & K Smallest
- k Closest Elements
- Max diff between two m Sized Subsets
- Check if Binary Tree is Heap
- Huffman Coding
- Nodes less than a value in a Min Heap.
- Connect n ropes with minimum cost
- K maximum sum combinations from two arrays
- K’th largest in a stream
- Largest triplet product in a stream
- k most frequent
- Min Heap to Max Heap
- Check for Min-Heap from Level Order
- BST to Min Heap
- K Closest Points to the Origin
Hard Problems
- The Skyline Problem
- Median in a stream
- K-th Largest Sum Subarray
- Sort by Frequency
- Merge k sorted arrays & Linked Lists
- Range Covering K Sorted Lists
- Prim's Minimum Spanning Tree
- Dijkstra's Shortest Path
- Sort numbers stored on different machines
- Largest Derangement of a Sequence
- Merge two binary Max Heaps
- Sum of all between k1’th and k2’th smallest
- A data structure with min and max
Other Types of Heaps
Quick Links:
- Top Interview Questions on Heap
- Practice Problems on Heap
- Quizzes on Heap
- Learn Data Structure and Algorithms | DSA Tutorial
Binary Heap Introduction
Visit Course


Binary Heap Introduction

