(Translated by https://www.hiragana.jp/)
Kruskal’s Minimum Spanning Tree (MST) Algorithm - GeeksforGeeks

Kruskal’s Minimum Spanning Tree (MST) Algorithm

Last Updated : 23 Jul, 2025

Try it on GfG Practice

A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected, and undirected graph is a spanning tree (no cycles and connects all vertices) that has minimum weight. The weight of a spanning tree is the sum of all edges in the tree.

In Kruskal's algorithm, we sort all edges of the given graph in increasing order. Then it keeps on adding new edges and nodes in the MST if the newly added edge does not form a cycle. It picks the minimum weighted edge at first and the maximum weighted edge at last. Thus we can say that it makes a locally optimal choice in each step in order to find the optimal solution. Hence this is a Greedy Algorithm.

How to find MST using Kruskal's algorithm?

Below are the steps for finding MST using Kruskal's algorithm:

Sort all the edges in a non-decreasing order of their weight.
Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If the cycle is not formed, include this edge. Else, discard it.
Repeat step 2 until there are (V-1) edges in the spanning tree.

Kruskal's Algorithm uses the Disjoint Set Data Structure to detect cycles.

Illustration:

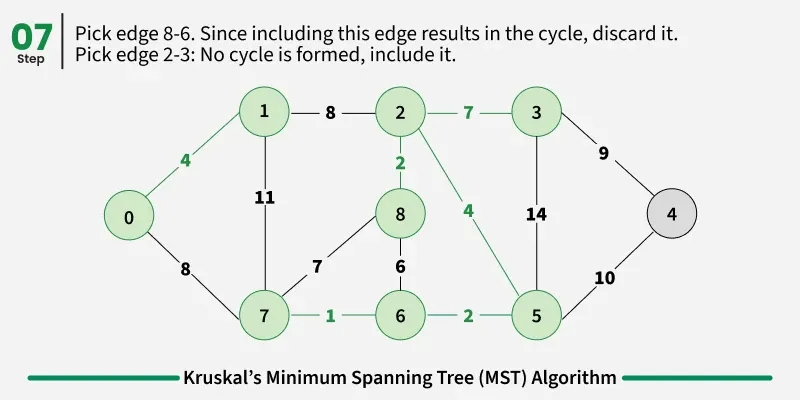
The graph contains 9 vertices and 14 edges. So, the minimum spanning tree formed will be having (9 - 1) = 8 edges.
1 / 10

C++

#include <bits/stdc++.h>
using namespace std;

// Disjoint set data struture
class DSU {
    vector<int> parent, rank;

public:
    DSU(int n) {
        parent.resize(n);
        rank.resize(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    int find(int i) {
        return (parent[i] == i) ? i : (parent[i] = find(parent[i]));
    }

    void unite(int x, int y) {
        int s1 = find(x), s2 = find(y);
        if (s1 != s2) {
            if (rank[s1] < rank[s2]) parent[s1] = s2;
            else if (rank[s1] > rank[s2]) parent[s2] = s1;
            else parent[s2] = s1, rank[s1]++;
        }
    }
};
bool comparator(vector<int> &a,vector<int> &b){
    if(a[2]<=b[2])return true;
    return false;
}
int kruskalsMST(int V, vector<vector<int>> &edges) {
    
    // Sort all edhes
    sort(edges.begin(), edges.end(),comparator);
    
    // Traverse edges in sorted order
    DSU dsu(V);
    int cost = 0, count = 0;
    
    for (auto &e : edges) {
        int x = e[0], y = e[1], w = e[2];
        
        // Make sure that there is no cycle
        if (dsu.find(x) != dsu.find(y)) {
            dsu.unite(x, y);
            cost += w;
            if (++count == V - 1) break;
        }
    }
    return cost;
}

int main() {
    
    // An edge contains, weight, source and destination
    vector<vector<int>> edges = {
        {0, 1, 10}, {1, 3, 15}, {2, 3, 4}, {2, 0, 6}, {0, 3, 5}
    };
    
    cout<<kruskalsMST(4, edges);
    
    return 0;
}

C

// C code to implement Kruskal's algorithm

#include <stdio.h>
#include <stdlib.h>

// Comparator function to use in sorting
int comparator(const int p1[], const int p2[])
{
    return p1[2] - p2[2];
}

// Initialization of parent[] and rank[] arrays
void makeSet(int parent[], int rank[], int n)
{
    for (int i = 0; i < n; i++) {
        parent[i] = i;
        rank[i] = 0;
    }
}

// Function to find the parent of a node
int findParent(int parent[], int component)
{
    if (parent[component] == component)
        return component;

    return parent[component]
           = findParent(parent, parent[component]);
}

// Function to unite two sets
void unionSet(int u, int v, int parent[], int rank[], int n)
{
    // Finding the parents
    u = findParent(parent, u);
    v = findParent(parent, v);

    if (rank[u] < rank[v]) {
        parent[u] = v;
    }
    else if (rank[u] > rank[v]) {
        parent[v] = u;
    }
    else {
        parent[v] = u;

        // Since the rank increases if
        // the ranks of two sets are same
        rank[u]++;
    }
}

// Function to find the MST
int kruskalAlgo(int n, int edge[n][3])
{
    // First we sort the edge array in ascending order
    // so that we can access minimum distances/cost
    qsort(edge, n, sizeof(edge[0]), comparator);

    int parent[n];
    int rank[n];

    // Function to initialize parent[] and rank[]
    makeSet(parent, rank, n);

    // To store the minimun cost
    int minCost = 0;
    for (int i = 0; i < n; i++) {
        int v1 = findParent(parent, edge[i][0]);
        int v2 = findParent(parent, edge[i][1]);
        int wt = edge[i][2];

        // If the parents are different that
        // means they are in different sets so
        // union them
        if (v1 != v2) {
            unionSet(v1, v2, parent, rank, n);
            minCost += wt;
        }
    }

    return minCost;
}

// Driver code
int main()
{
    int edge[5][3] = { { 0, 1, 10 },
                       { 0, 2, 6 },
                       { 0, 3, 5 },
                       { 1, 3, 15 },
                       { 2, 3, 4 } };

    printf("%d",kruskalAlgo(5, edge));

    return 0;
}

Java

import java.util.Arrays;
import java.util.Comparator;

class GfG {
    public static int kruskalsMST(int V, int[][] edges) {
        
        // Sort all edges based on weight
        Arrays.sort(edges, Comparator.comparingInt(e -> e[2]));
        
        // Traverse edges in sorted order
        DSU dsu = new DSU(V);
        int cost = 0, count = 0;
        
        for (int[] e : edges) {
            int x = e[0], y = e[1], w = e[2];
            
            // Make sure that there is no cycle
            if (dsu.find(x) != dsu.find(y)) {
                dsu.union(x, y);
                cost += w;
                if (++count == V - 1) break;
            }
        }
        return cost;
    }

    public static void main(String[] args) {
        
        // An edge contains, weight, source and destination
        int[][] edges = {
            {0, 1, 10}, {1, 3, 15}, {2, 3, 4}, {2, 0, 6}, {0, 3, 5}
        };
        
       System.out.println(kruskalsMST(4, edges));
    }
}

// Disjoint set data structure
class DSU {
    private int[] parent, rank;

    public DSU(int n) {
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    public int find(int i) {
        if (parent[i] != i) {
            parent[i] = find(parent[i]);
        }
        return parent[i];
    }

    public void union(int x, int y) {
        int s1 = find(x);
        int s2 = find(y);
        if (s1 != s2) {
            if (rank[s1] < rank[s2]) {
                parent[s1] = s2;
            } else if (rank[s1] > rank[s2]) {
                parent[s2] = s1;
            } else {
                parent[s2] = s1;
                rank[s1]++;
            }
        }
    }
}

Python

from functools import cmp_to_key

def comparator(a,b):
    return a[2] - b[2];

def kruskals_mst(V, edges):

    # Sort all edges
    edges = sorted(edges,key=cmp_to_key(comparator))
    
    # Traverse edges in sorted order
    dsu = DSU(V)
    cost = 0
    count = 0
    for x, y, w in edges:
        
        # Make sure that there is no cycle
        if dsu.find(x) != dsu.find(y):
            dsu.union(x, y)
            cost += w
            count += 1
            if count == V - 1:
                break
    return cost
    
# Disjoint set data structure
class DSU:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [1] * n

    def find(self, i):
        if self.parent[i] != i:
            self.parent[i] = self.find(self.parent[i])
        return self.parent[i]

    def union(self, x, y):
        s1 = self.find(x)
        s2 = self.find(y)
        if s1 != s2:
            if self.rank[s1] < self.rank[s2]:
                self.parent[s1] = s2
            elif self.rank[s1] > self.rank[s2]:
                self.parent[s2] = s1
            else:
                self.parent[s2] = s1
                self.rank[s1] += 1


if __name__ == '__main__':
    
    # An edge contains, weight, source and destination
    edges = [[0, 1, 10], [1, 3, 15], [2, 3, 4], [2, 0, 6], [0, 3, 5]]
    print(kruskals_mst(4, edges))

C#

// Using System.Collections.Generic;
using System;

class GfG {
    public static int KruskalsMST(int V, int[][] edges) {
        // Sort all edges based on weight
        Array.Sort(edges, (e1, e2) => e1[2].CompareTo(e2[2]));
        
        // Traverse edges in sorted order
        DSU dsu = new DSU(V);
        int cost = 0, count = 0;
        
        foreach (var e in edges) {
            int x = e[0], y = e[1], w = e[2];
            
            // Make sure that there is no cycle
            if (dsu.Find(x) != dsu.Find(y)) {
                dsu.Union(x, y);
                cost += w;
                if (++count == V - 1) break;
            }
        }
        return cost;
    }

    public static void Main(string[] args) {
        // An edge contains, weight, source and destination
        int[][] edges = {
            new int[] {0, 1, 10}, new int[] {1, 3, 15}, new int[] {2, 3, 4}, new int[] {2, 0, 6}, new int[] {0, 3, 5}
        };
        
        Console.WriteLine(KruskalsMST(4, edges));
    }
}

// Disjoint set data structure
class DSU {
    private int[] parent, rank;

    public DSU(int n) {
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    public int Find(int i) {
        if (parent[i] != i) {
            parent[i] = Find(parent[i]);
        }
        return parent[i];
    }

    public void Union(int x, int y) {
        int s1 = Find(x);
        int s2 = Find(y);
        if (s1 != s2) {
            if (rank[s1] < rank[s2]) {
                parent[s1] = s2;
            } else if (rank[s1] > rank[s2]) {
                parent[s2] = s1;
            } else {
                parent[s2] = s1;
                rank[s1]++;
            }
        }
    }
}

JavaScript

function kruskalsMST(V, edges) {
    
    // Sort all edges
    edges.sort((a, b) => a[2] - b[2]);
    
    // Traverse edges in sorted order
    const dsu = new DSU(V);
    let cost = 0;
    let count = 0;
    for (const [x, y, w] of edges) {
        
        // Make sure that there is no cycle
        if (dsu.find(x) !== dsu.find(y)) {
            dsu.unite(x, y);
            cost += w;
            if (++count === V - 1) break;
        }
    }
    return cost;
}

// Disjoint set data structure
class DSU {
    constructor(n) {
        this.parent = Array.from({ length: n }, (_, i) => i);
        this.rank = Array(n).fill(1);
    }

    find(i) {
        if (this.parent[i] !== i) {
            this.parent[i] = this.find(this.parent[i]);
        }
        return this.parent[i];
    }

    unite(x, y) {
        const s1 = this.find(x);
        const s2 = this.find(y);
        if (s1 !== s2) {
            if (this.rank[s1] < this.rank[s2]) this.parent[s1] = s2;
            else if (this.rank[s1] > this.rank[s2]) this.parent[s2] = s1;
            else {
                this.parent[s2] = s1;
                this.rank[s1]++;
            }
        }
    }
}

const edges = [
    [0, 1, 10], [1, 3, 15], [2, 3, 4], [2, 0, 6], [0, 3, 5]
];
console.log(kruskalsMST(4, edges));

Output

Following are the edges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Minimum Cost Spanning Tree: 19

Time Complexity: O(E * log E) or O(E * log V)

Sorting of edges takes O(E*logE) time.
After sorting, we iterate through all edges and apply the find-union algorithm. The find and union operations can take at most O(logV) time.
So overall complexity is O(E*logE + E*logV) time.
The value of E can be at most O(V²), so O(logV) and O(logE) are the same. Therefore, the overall time complexity is O(E * logE) or O(E*logV)

Auxiliary Space: O(E+V), where V is the number of vertices and E is the number of edges in the graph.

Problems based on Minimum Spanning Tree

Kruskal’s Algorithm for Minimum Spanning Tree

K

kartik

Improve

Article Tags :

Practice Tags :

Similar Reads