Maximum Subarray Sum - Kadane's Algorithm

Given an integer array arr[], find the subarray (containing at least one element) which has the maximum possible sum, and return that sum.
Note: A subarray is a continuous part of an array.
Examples:
Input: arr[] = [2, 3, -8, 7, -1, 2, 3]
Output: 11
Explanation: The subarray [7, -1, 2, 3] has the largest sum 11.Input: arr[] = [-2, -4]
Output: -2
Explanation: The subarray [-2] has the largest sum -2.Input: arr[] = [5, 4, 1, 7, 8]
Output: 25
Explanation: The subarray [5, 4, 1, 7, 8] has the largest sum 25.
Table of Content
[Naive Approach] By iterating over all subarrays - O(n^2) Time and O(1) Space
The idea is to run two nested loops to iterate over all possible subarrays and find the maximum sum. The outer loop will mark the starting point of a subarray and inner loop will mark the ending point of the subarray.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int maxSubarraySum(vector<int> &arr) {
int res = arr[0];
// Outer loop for starting point of subarray
for(int i = 0; i < arr.size(); i++) {
int currSum = 0;
// Inner loop for ending point of subarray
for(int j = i; j < arr.size(); j++) {
currSum = currSum + arr[j];
// Update res if currSum is greater than res
res = max(res, currSum);
}
}
return res;
}
int main() {
vector<int> arr = {2, 3, -8, 7, -1, 2, 3};
cout << maxSubarraySum(arr);
return 0;
}
using namespace std;int maxSubarraySum(vector<int> &arr) { int res = arr[0]; // Outer loop for starting point of subarray for(int i = 0; i < arr.size(); i++) { int currSum = 0; // Inner loop for ending point of subarray for(int j = i; j < arr.size(); j++) { currSum = currSum + arr[j]; // Update res if currSum is greater than res res = max(res, currSum); } } return res;}int main() { vector<int> arr = {2, 3, -8, 7, -1, 2, 3}; cout << maxSubarraySum(arr); return 0;}#include <stdio.h>
int maxSubarraySum(int arr[], int size) {
int maxSum = arr[0];
// Outer loop for starting point of subarray
for (int i = 0; i < size; i++) {
int currSum = 0;
// Inner loop for ending point of subarray
for (int j = i; j < size; j++) {
currSum = currSum + arr[j];
// Update maxSum if currSum is greater than maxSum
if (currSum > maxSum) {
maxSum = currSum;
}
}
}
return maxSum;
}
int main() {
int arr[] = {2, 3, -8, 7, -1, 2, 3};
int size = sizeof(arr) / sizeof(arr[0]);
printf("%d", maxSubarraySum(arr, size));
return 0;
}
import java.util.Arrays;
class GfG {
static int maxSubarraySum(int[] arr) {
int res = arr[0];
// Outer loop for starting point of subarray
for (int i = 0; i < arr.length; i++) {
int currSum = 0;
// Inner loop for ending point of subarray
for (int j = i; j < arr.length; j++) {
currSum = currSum + arr[j];
// Update res if currSum is greater than res
res = Math.max(res, currSum);
}
}
return res;
}
public static void main(String[] args) {
int[] arr = {2, 3, -8, 7, -1, 2, 3};
System.out.println(maxSubarraySum(arr));
}
}
def maxSubarraySum(arr):
res = arr[0]
# Outer loop for starting point of subarray
for i in range(len(arr)):
currSum = 0
# Inner loop for ending point of subarray
for j in range(i, len(arr)):
currSum = currSum + arr[j]
# Update res if currSum is greater than res
res = max(res, currSum)
return res
if __name__ == "__main__":
arr = [2, 3, -8, 7, -1, 2, 3]
print(maxSubarraySum(arr))
using System;
class GfG {
static int maxSubarraySum(int[] arr) {
int res = arr[0];
// Outer loop for starting point of subarray
for (int i = 0; i < arr.Length; i++) {
int currSum = 0;
// Inner loop for ending point of subarray
for (int j = i; j < arr.Length; j++) {
currSum = currSum + arr[j];
// Update res if currSum is greater than res
res = Math.Max(res, currSum);
}
}
return res;
}
static void Main() {
int[] arr = {2, 3, -8, 7, -1, 2, 3};
Console.WriteLine(maxSubarraySum(arr));
}
}
function maxSubarraySum(arr) {
let res = arr[0];
// Outer loop for starting point of subarray
for (let i = 0; i < arr.length; i++) {
let currSum = 0;
// Inner loop for ending point of subarray
for (let j = i; j < arr.length; j++) {
currSum = currSum + arr[j];
// Update res if currSum is greater than res
res = Math.max(res, currSum);
}
}
return res;
}
const arr = [2, 3, -8, 7, -1, 2, 3];
console.log(maxSubarraySum(arr));
Output
11
[Expected Approach] Using Kadane's Algorithm - O(n) Time and O(1) Space
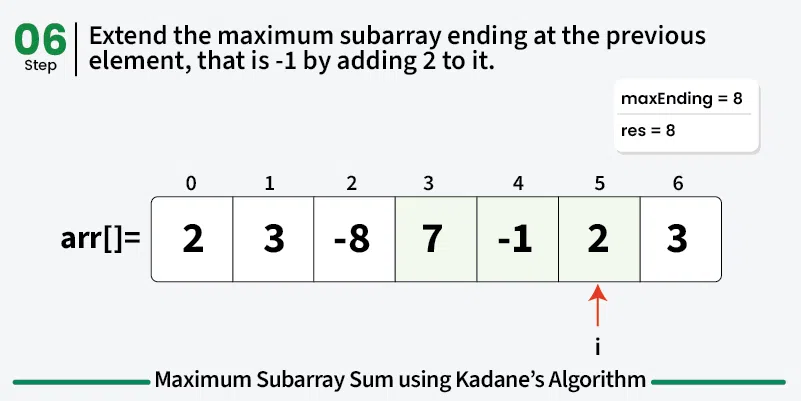
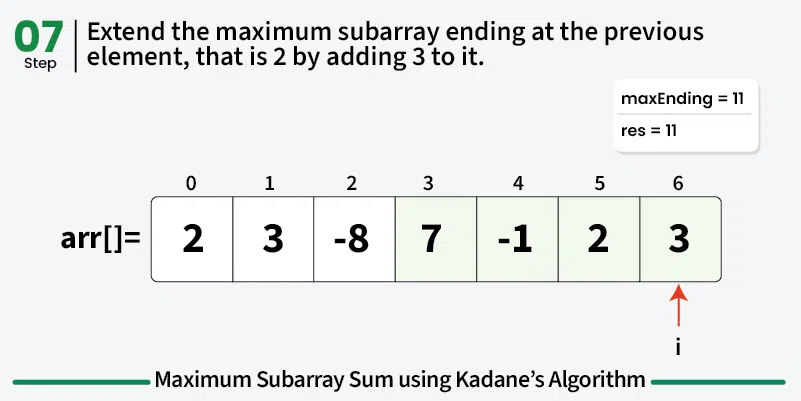
The idea of Kadane's algorithm is to traverse over the array from left to right and for each element, find the maximum sum among all subarrays ending at that element. The result will be the maximum of all these values.
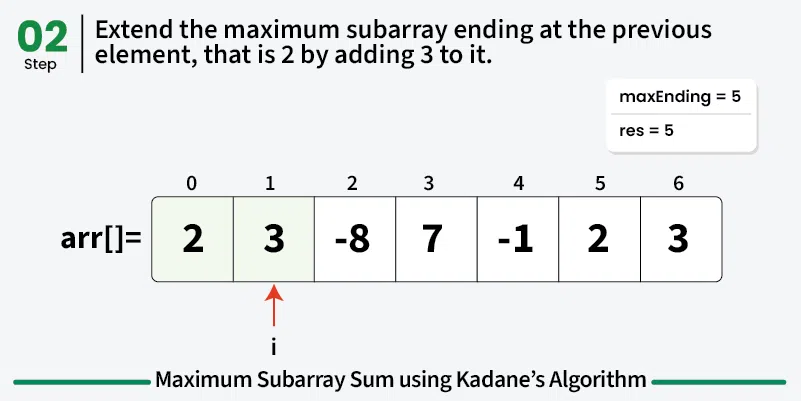
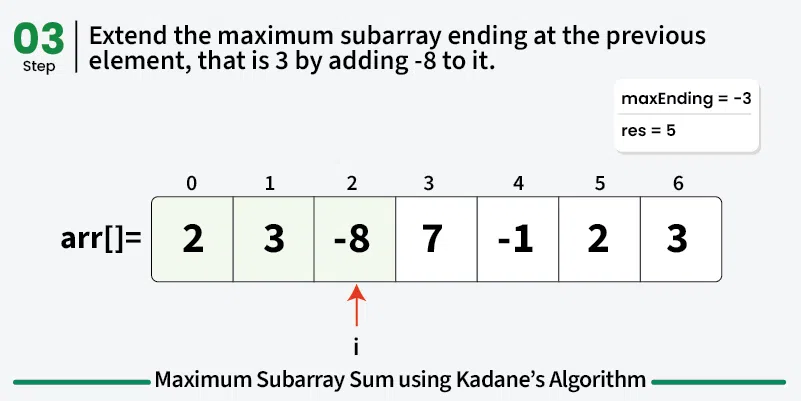
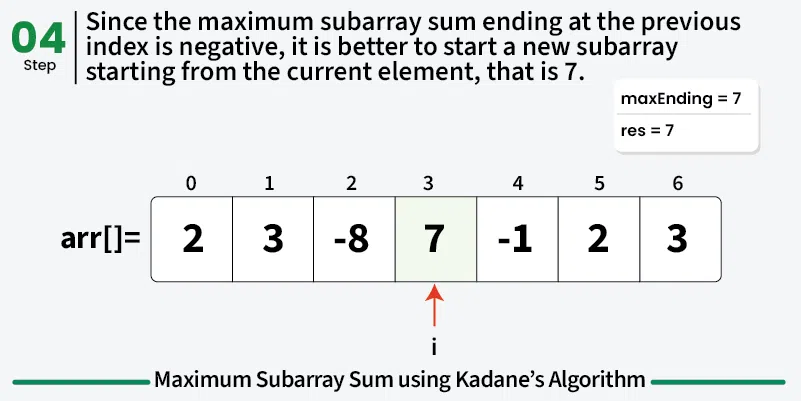
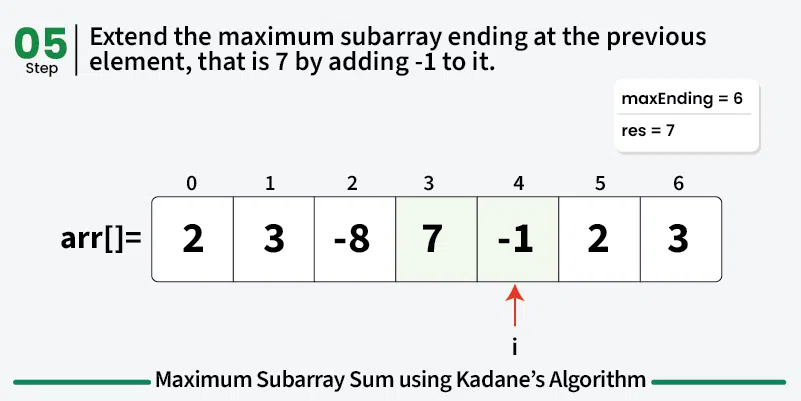
To calculate the maximum sum of subarray ending at current element, say maxEnding, we can use the maximum sum ending at the previous element.
So for any element, we have two choices:
Choice 1: Extend the maximum sum subarray ending at the previous element by adding the current element to it. If the maximum subarray sum ending at the previous index is positive, then it is always better to extend the subarray.
Choice 2: Start a new subarray starting from the current element. If the maximum subarray sum ending at the previous index is negative, it is always better to start a new subarray from the current element.
This means that maxEnding at index i = max(maxEnding at index (i - 1) + arr[i], arr[i]) and the maximum value of maxEnding at any index will be our answer.
Illustration:








#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int maxSubarraySum(vector<int> &arr) {
// Stores the result (maximum sum found so far)
int res = arr[0];
// Maximum sum of subarray ending at current position
int maxEnding = arr[0];
for (int i = 1; i < arr.size(); i++) {
// Either extend the previous subarray or start
// new from current element
maxEnding = max(arr[i], maxEnding + arr[i]);
// Update result if the new subarray sum is larger
res = max(res, maxEnding);
}
return res;
}
int main() {
vector<int> arr = {2, 3, -8, 7, -1, 2, 3};
cout << maxSubarraySum(arr);
return 0;
}
using namespace std;int maxSubarraySum(vector<int> &arr) { // Stores the result (maximum sum found so far) int res = arr[0]; // Maximum sum of subarray ending at current position int maxEnding = arr[0]; for (int i = 1; i < arr.size(); i++) { // Either extend the previous subarray or start // new from current element maxEnding = max(arr[i], maxEnding + arr[i]); // Update result if the new subarray sum is larger res = max(res, maxEnding); } return res;}int main() { vector<int> arr = {2, 3, -8, 7, -1, 2, 3}; cout << maxSubarraySum(arr); return 0;}#include <stdio.h>
#include <limits.h>
int maxSubarraySum(int arr[], int size) {
// Stores the result (maximum sum found so far)
int res = arr[0];
// Maximum sum of subarray ending at current position
int maxEnding = arr[0];
for (int i = 1; i < size; i++) {
// Either extend the previous subarray or start
// new from current element
maxEnding = (maxEnding + arr[i] > arr[i]) ?
maxEnding + arr[i] : arr[i];
// Update result if the new subarray sum is larger
res = (res > maxEnding) ? res : maxEnding;
}
return res;
}
int main() {
int arr[] = {2, 3, -8, 7, -1, 2, 3};
int size = sizeof(arr) / sizeof(arr[0]);
printf("%lld\n", maxSubarraySum(arr, size));
return 0;
}
import java.util.Arrays;
class GfG {
static int maxSubarraySum(int[] arr) {
// Stores the result (maximum sum found so far)
int res = arr[0];
// Maximum sum of subarray ending at current position
int maxEnding = arr[0];
for (int i = 1; i < arr.length; i++) {
// Either extend the previous subarray or start
// new from current element
maxEnding = Math.max(maxEnding + arr[i], arr[i]);
// Update result if the new subarray sum is larger
res = Math.max(res, maxEnding);
}
return res;
}
public static void main(String[] args) {
int[] arr = {2, 3, -8, 7, -1, 2, 3};
System.out.println(maxSubarraySum(arr));
}
}
def maxSubarraySum(arr):
# Stores the result (maximum sum found so far)
res = arr[0]
# Maximum sum of subarray ending at current position
maxEnding = arr[0]
for i in range(1, len(arr)):
# Either extend the previous subarray or start
# new from current element
maxEnding = max(maxEnding + arr[i], arr[i])
# Update result if the new subarray sum is larger
res = max(res, maxEnding)
return res
if __name__ == "__main__":
arr = [2, 3, -8, 7, -1, 2, 3]
print(maxSubarraySum(arr))
using System;
class GfG {
static int maxSubarraySum(int[] arr) {
// Stores the result (maximum sum found so far)
int res = arr[0];
// Maximum sum of subarray ending at current position
int maxEnding = arr[0];
for (int i = 1; i < arr.Length; i++) {
// Either extend the previous subarray or start
// new from current element
maxEnding = Math.Max(maxEnding + arr[i], arr[i]);
// Update result if the new subarray sum is larger
res = Math.Max(res, maxEnding);
}
return res;
}
static void Main() {
int[] arr = { 2, 3, -8, 7, -1, 2, 3 };
Console.WriteLine(maxSubarraySum(arr));
}
}
function maxSubarraySum(arr) {
// Stores the result (maximum sum found so far)
let res = arr[0];
// Maximum sum of subarray ending at current position
let maxEnding = arr[0];
for (let i = 1; i < arr.length; i++) {
// Either extend the previous subarray or start
// new from current element
maxEnding = Math.max(maxEnding + arr[i], arr[i]);
// Update result if the new subarray sum is larger
res = Math.max(res, maxEnding);
}
return res;
}
// Driver Code
const arr = [2, 3, -8, 7, -1, 2, 3];
console.log(maxSubarraySum(arr));
Output
11
Related Articles:
- Print the Maximum Sum Subarray
- Maximum Product Subarray
- Max subarray sum with repeated concatenations


Maximum Subarray Sum

