Prim’s Algorithm for Minimum Spanning Tree (MST)

Prim’s algorithm is a Greedy algorithm like Kruskal's algorithm. This algorithm always starts with a single node and moves through several adjacent nodes, in order to explore all of the connected edges along the way.
- The algorithm starts with an empty spanning tree.
- The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, and the other set contains the vertices not yet included.
- At every step, it considers all the edges that connect the two sets and picks the minimum weight edge from these edges. After picking the edge, it moves the other endpoint of the edge to the set containing MST.
A group of edges that connects two sets of vertices in a graph is called Articulation Points (or Cut Vertices) in graph theory. So, at every step of Prim’s algorithm, find a cut, pick the minimum weight edge from the cut, and include this vertex in MST Set (the set that contains already included vertices).
Working of the Prim's Algorithm
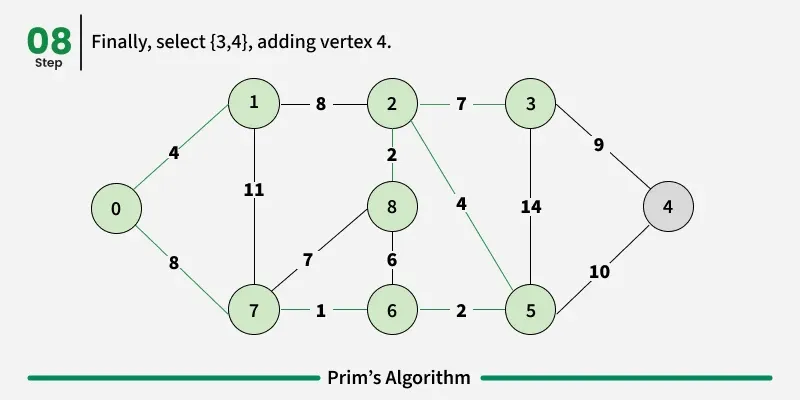
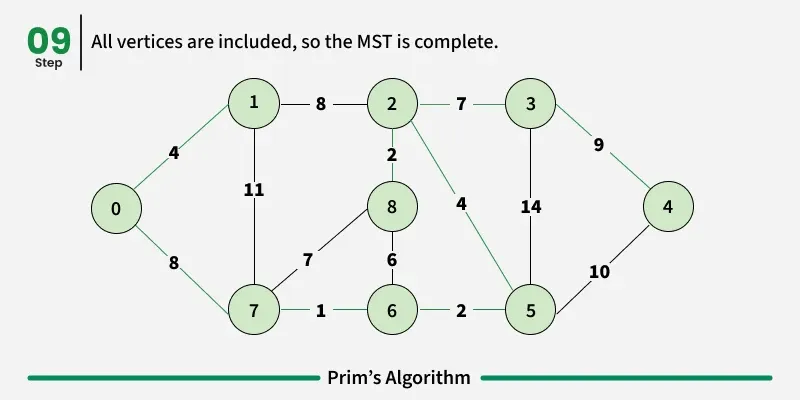
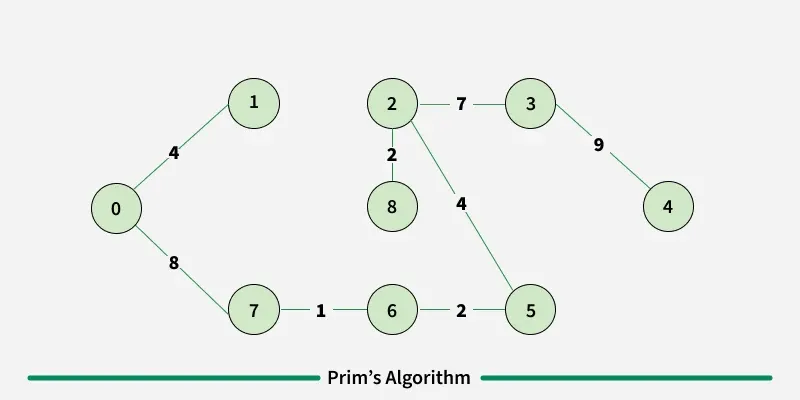
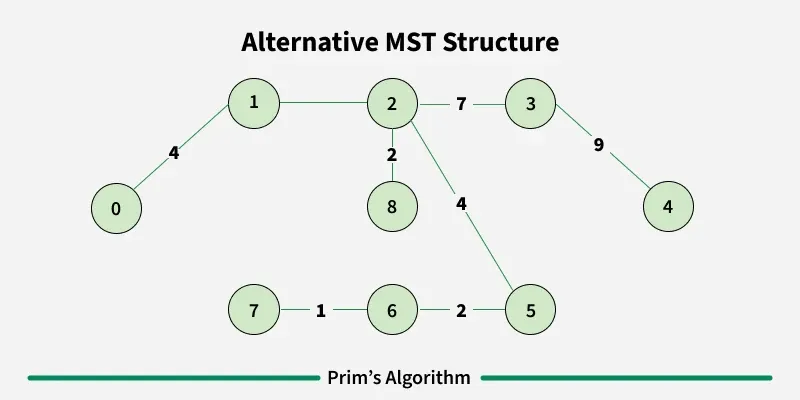
Step 1: Determine an arbitrary vertex as the starting vertex of the MST. We pick 0 in the below diagram.
Step 2: Follow steps 3 to 5 till there are vertices that are not included in the MST (known as fringe vertex).
Step 3: Find edges connecting any tree vertex with the fringe vertices.
Step 4: Find the minimum among these edges.
Step 5: Add the chosen edge to the MST. Since we consider only the edges that connect fringe vertices with the rest, we never get a cycle.
Step 6: Return the MST and exit
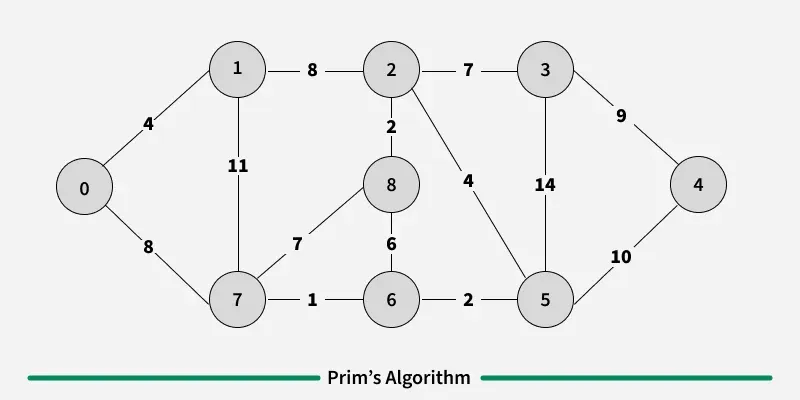

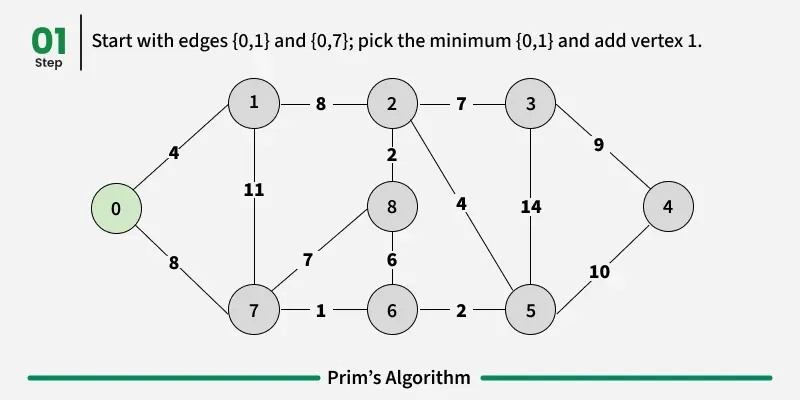

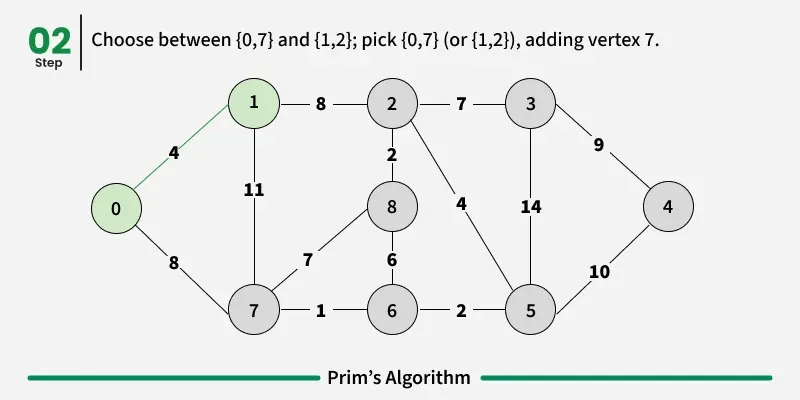

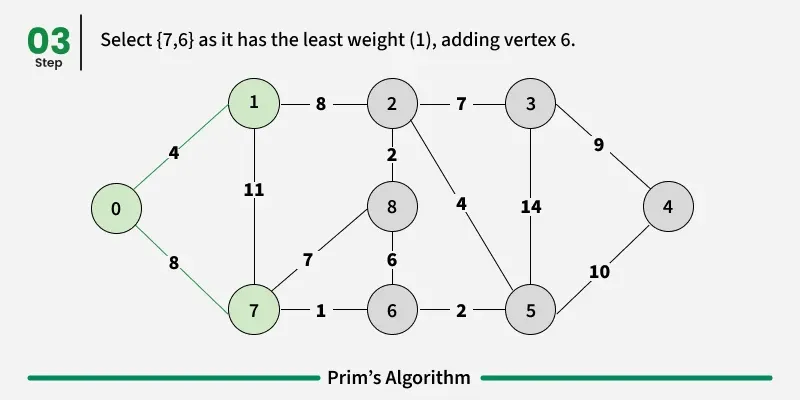

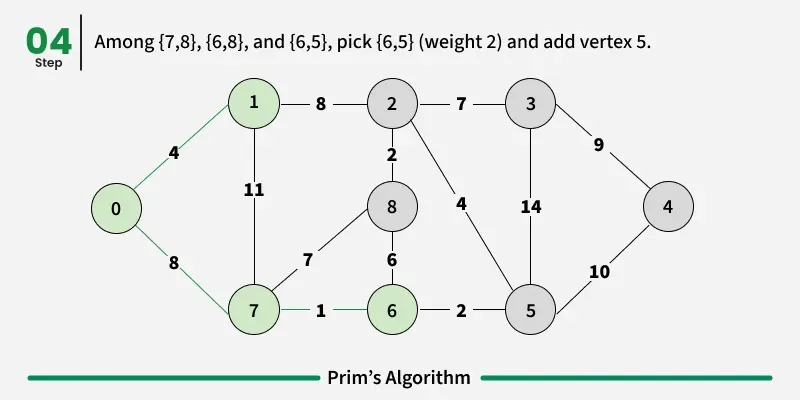

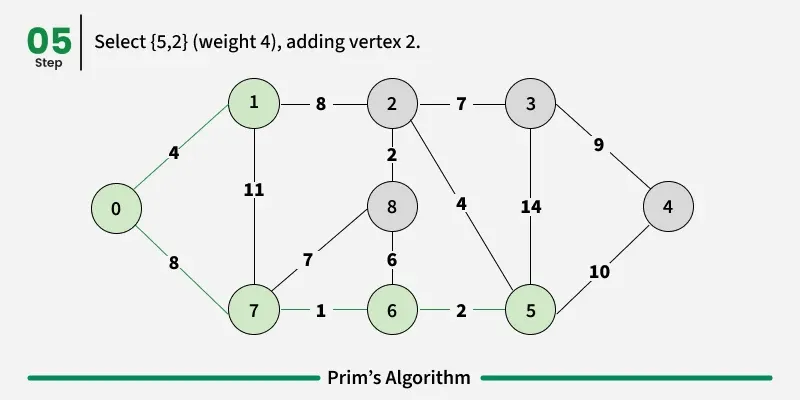

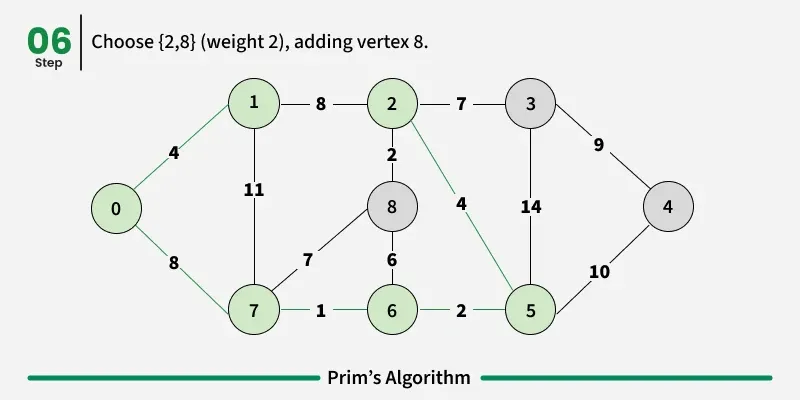

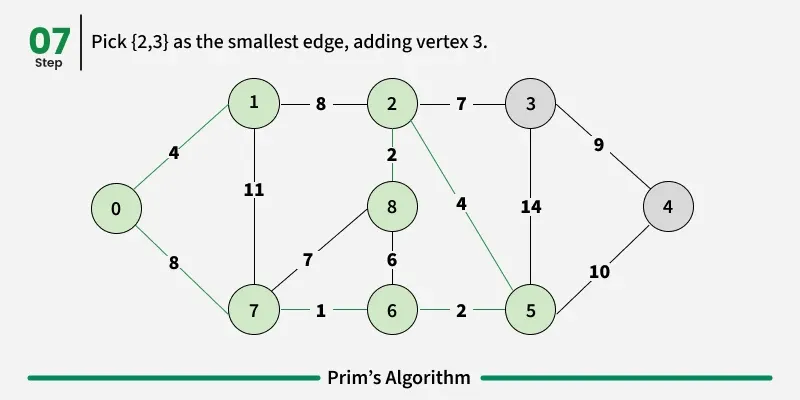





How to implement Prim's Algorithm?
Follow the given steps to utilize the Prim's Algorithm mentioned above for finding MST of a graph:
- Create a set mstSet that keeps track of vertices already included in MST.
- Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign the key value as 0 for the first vertex so that it is picked first.
- While mstSet doesn't include all vertices
- Pick a vertex u that is not there in mstSet and has a minimum key value.
- Include u in the mstSet.
- Update the key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices. For every adjacent vertex v, if the weight of edge u-v is less than the previous key value of v, update the key value as the weight of u-v.
The idea of using key values is to pick the minimum weight edge from the cut. The key values are used only for vertices that are not yet included in MST, the key value for these vertices indicates the minimum weight edges connecting them to the set of vertices included in MST.
Below is the implementation of the approach:
// A C++ program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
#include <bits/stdc++.h>
using namespace std;
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey(vector<int> &key, vector<bool> &mstSet) {
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < mstSet.size(); v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
void printMST(vector<int> &parent, vector<vector<int>> &graph) {
cout << "Edge \tWeight\n";
for (int i = 1; i < graph.size(); i++)
cout << parent[i] << " - " << i << " \t"
<< graph[parent[i]][i] << " \n";
}
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST(vector<vector<int>> &graph) {
int V = graph.size();
// Array to store constructed MST
vector<int> parent(V);
// Key values used to pick minimum weight edge in cut
vector<int> key(V);
// To represent set of vertices included in MST
vector<bool> mstSet(V);
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is picked as first
// vertex.
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the
// set of vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of
// the adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for vertices
// not yet included in MST Update the key only
// if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false
&& graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// Print the constructed MST
printMST(parent, graph);
}
// Driver's code
int main() {
vector<vector<int>> graph = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
primMST(graph);
return 0;
}
// A C++ program for Prim's Minimum// Spanning Tree (MST) algorithm. The program is// for adjacency matrix representation of the graphusing namespace std;// A utility function to find the vertex with// minimum key value, from the set of vertices// not yet included in MSTint minKey(vector<int> &key, vector<bool> &mstSet) { // Initialize min value int min = INT_MAX, min_index; for (int v = 0; v < mstSet.size(); v++) if (mstSet[v] == false && key[v] < min) min = key[v], min_index = v; return min_index;}// A utility function to print the// constructed MST stored in parent[]void printMST(vector<int> &parent, vector<vector<int>> &graph) { cout << "Edge \tWeight\n"; for (int i = 1; i < graph.size(); i++) cout << parent[i] << " - " << i << " \t" << graph[parent[i]][i] << " \n";}// Function to construct and print MST for// a graph represented using adjacency// matrix representationvoid primMST(vector<vector<int>> &graph) { int V = graph.size(); // Array to store constructed MST vector<int> parent(V); // Key values used to pick minimum weight edge in cut vector<int> key(V); // To represent set of vertices included in MST vector<bool> mstSet(V); // Initialize all keys as INFINITE for (int i = 0; i < V; i++) key[i] = INT_MAX, mstSet[i] = false; // Always include first 1st vertex in MST. // Make key 0 so that this vertex is picked as first // vertex. key[0] = 0; // First node is always root of MST parent[0] = -1; // The MST will have V vertices for (int count = 0; count < V - 1; count++) { // Pick the minimum key vertex from the // set of vertices not yet included in MST int u = minKey(key, mstSet); // Add the picked vertex to the MST Set mstSet[u] = true; // Update key value and parent index of // the adjacent vertices of the picked vertex. // Consider only those vertices which are not // yet included in MST for (int v = 0; v < V; v++) // graph[u][v] is non zero only for adjacent // vertices of m mstSet[v] is false for vertices // not yet included in MST Update the key only // if graph[u][v] is smaller than key[v] if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) parent[v] = u, key[v] = graph[u][v]; } // Print the constructed MST printMST(parent, graph);}// Driver's codeint main() { vector<vector<int>> graph = { { 0, 2, 0, 6, 0 }, { 2, 0, 3, 8, 5 }, { 0, 3, 0, 0, 7 }, { 6, 8, 0, 0, 9 }, { 0, 5, 7, 9, 0 } }; // Print the solution primMST(graph); return 0;}// A C program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
#include <limits.h>
#include <stdbool.h>
#include <stdio.h>
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
int printMST(int parent[], int graph[V][V])
{
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i,
graph[parent[i]][i]);
}
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
// Array to store constructed MST
int parent[V];
// Key values used to pick minimum weight edge in cut
int key[V];
// To represent set of vertices included in MST
bool mstSet[V];
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is picked as first
// vertex.
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the
// set of vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of
// the adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for vertices
// not yet included in MST Update the key only
// if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false
&& graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// print the constructed MST
printMST(parent, graph);
}
// Driver's code
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
primMST(graph);
return 0;
}
// A Java program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency matrix
// representation of the graph
import java.io.*;
import java.lang.*;
import java.util.*;
class MST {
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
int minKey(int key[], Boolean mstSet[])
{
// Initialize min value
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < mstSet.length; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
// A utility function to print the constructed MST
// stored in parent[]
void printMST(int parent[], int graph[][])
{
System.out.println("Edge \tWeight");
for (int i = 1; i < graph.length; i++)
System.out.println(parent[i] + " - " + i + "\t"
+ graph[parent[i]][i]);
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
void primMST(int graph[][])
{
int V = graph.length;
// Array to store constructed MST
int parent[] = new int[V];
// Key values used to pick minimum weight edge in
// cut
int key[] = new int[V];
// To represent set of vertices included in MST
Boolean mstSet[] = new Boolean[V];
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is
// picked as first vertex
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for
// vertices not yet included in MST Update
// the key only if graph[u][v] is smaller
// than key[v]
if (graph[u][v] != 0 && mstSet[v] == false
&& graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
// Print the constructed MST
printMST(parent, graph);
}
public static void main(String[] args)
{
MST t = new MST();
int graph[][] = new int[][] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
t.primMST(graph);
}
}
# A Python3 program for
# Prim's Minimum Spanning Tree (MST) algorithm.
# The program is for adjacency matrix
# representation of the graph
# Library for INT_MAX
import sys
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
# A utility function to print
# the constructed MST stored in parent[]
def printMST(self, parent):
print("Edge \tWeight")
for i in range(1, self.V):
print(parent[i], "-", i, "\t", self.graph[parent[i]][i])
# A utility function to find the vertex with
# minimum distance value, from the set of vertices
# not yet included in shortest path tree
def minKey(self, key, mstSet):
# Initialize min value
min = sys.maxsize
for v in range(self.V):
if key[v] < min and mstSet[v] == False:
min = key[v]
min_index = v
return min_index
# Function to construct and print MST for a graph
# represented using adjacency matrix representation
def primMST(self):
# Key values used to pick minimum weight edge in cut
key = [sys.maxsize] * self.V
parent = [None] * self.V # Array to store constructed MST
# Make key 0 so that this vertex is picked as first vertex
key[0] = 0
mstSet = [False] * self.V
parent[0] = -1 # First node is always the root of
for cout in range(self.V):
# Pick the minimum distance vertex from
# the set of vertices not yet processed.
# u is always equal to src in first iteration
u = self.minKey(key, mstSet)
# Put the minimum distance vertex in
# the shortest path tree
mstSet[u] = True
# Update dist value of the adjacent vertices
# of the picked vertex only if the current
# distance is greater than new distance and
# the vertex in not in the shortest path tree
for v in range(self.V):
# graph[u][v] is non zero only for adjacent vertices of m
# mstSet[v] is false for vertices not yet included in MST
# Update the key only if graph[u][v] is smaller than key[v]
if self.graph[u][v] > 0 and mstSet[v] == False \
and key[v] > self.graph[u][v]:
key[v] = self.graph[u][v]
parent[v] = u
self.printMST(parent)
# Driver's code
if __name__ == '__main__':
g = Graph(5)
g.graph = [[0, 2, 0, 6, 0],
[2, 0, 3, 8, 5],
[0, 3, 0, 0, 7],
[6, 8, 0, 0, 9],
[0, 5, 7, 9, 0]]
g.primMST()
// A C# program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency matrix
// representation of the graph
using System;
using System.Collections.Generic;
class MST
{
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
int MinKey(int[] key, bool[] mstSet)
{
// Initialize min value
int min = int.MaxValue, minIndex = -1;
for (int v = 0; v < mstSet.Length; v++)
if (!mstSet[v] && key[v] < min)
{
min = key[v];
minIndex = v;
}
return minIndex;
}
// A utility function to print the constructed MST
// stored in parent[]
void PrintMST(int[] parent, int[,] graph)
{
Console.WriteLine("Edge \tWeight");
for (int i = 1; i < graph.GetLength(0); i++)
Console.WriteLine(parent[i] + " - " + i + "\t" + graph[parent[i], i]);
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
public void PrimMST(int[,] graph)
{
int V = graph.GetLength(0);
// Array to store constructed MST
int[] parent = new int[V];
// Key values used to pick minimum weight edge in
// cut
int[] key = new int[V];
// To represent set of vertices included in MST
bool[] mstSet = new bool[V];
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
{
key[i] = int.MaxValue;
mstSet[i] = false;
}
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is
// picked as first vertex
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for (int count = 0; count < V - 1; count++)
{
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
int u = MinKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for
// vertices not yet included in MST Update
// the key only if graph[u][v] is smaller
// than key[v]
if (graph[u, v] != 0 && !mstSet[v] && graph[u, v] < key[v])
{
parent[v] = u;
key[v] = graph[u, v];
}
}
// Print the constructed MST
PrintMST(parent, graph);
}
public static void Main(string[] args)
{
MST t = new MST();
int[,] graph = new int[,] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
t.PrimMST(graph);
}
}
// Number of vertices in the graph
let V = 5;
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
function minKey(key, mstSet) {
// Initialize min value
let min = Number.MAX_VALUE, min_index = -1;
for (let v = 0; v < V; v++)
if (!mstSet[v] && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
function printMST(parent, graph) {
console.log("Edge Weight");
for (let i = 1; i < V; i++)
console.log(parent[i] + " - " + i + " " + graph[parent[i]][i]);
}
// Function to construct and print MST for
// a graph represented using adjacency matrix
function primMST(graph) {
// Array to store constructed MST
let parent = new Array(V);
// Key values used to pick minimum weight edge in cut
let key = new Array(V);
// To represent set of vertices included in MST
let mstSet = new Array(V);
// Initialize all keys as INFINITE
for (let i = 0; i < V; i++) {
key[i] = Number.MAX_VALUE;
mstSet[i] = false;
}
// Always include first vertex in MST.
key[0] = 0;
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (let count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of vertices not yet included in MST
let u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the adjacent vertices of the picked vertex.
for (let v = 0; v < V; v++) {
// graph[u][v] is non-zero only for adjacent vertices of u
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
// Print the constructed MST
printMST(parent, graph);
}
// Driver code
let graph = [
[ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ]
];
// Print the solution
primMST(graph);
Output
Edge Weight 0 - 1 2 1 - 2 3 0 - 3 6 1 - 4 5
Time Complexity: O(V2), As, we are using adjacency matrix, if the input graph is represented using an adjacency list, then the time complexity of Prim's algorithm can be reduced to O((E+V) * logV) with the help of a binary heap.
Auxiliary Space: O(V)
Optimized Implementation using Adjacency List Representation (of Graph) and Priority Queue
- We transform the adjacency matrix into adjacency list using ArrayList<ArrayList<Integer>>. in Java, list of list in Python
and array of vectors in C++.- Then we create a Pair class to store the vertex and its weight .
- We sort the list on the basis of lowest weight.
- We create priority queue and push the first vertex and its weight in the queue
- Then we just traverse through its edges and store the least weight in a variable called ans.
- At last after all the vertex we return the ans.
#include<bits/stdc++.h>
using namespace std;
// Function to find sum of weights of edges of the Minimum Spanning Tree.
int spanningTree(int V, int E, vector<vector<int>> &edges) {
// Create an adjacency list representation of the graph
vector<vector<int>> adj[V];
// Fill the adjacency list with edges and their weights
for (int i = 0; i < E; i++) {
int u = edges[i][0];
int v = edges[i][1];
int wt = edges[i][2];
adj[u].push_back({v, wt});
adj[v].push_back({u, wt});
}
// Create a priority queue to store edges with their weights
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
// Create a visited array to keep track of visited vertices
vector<bool> visited(V, false);
// Variable to store the result (sum of edge weights)
int res = 0;
// Start with vertex 0
pq.push({0, 0});
// Perform Prim's algorithm to find the Minimum Spanning Tree
while(!pq.empty()){
auto p = pq.top();
pq.pop();
int wt = p.first; // Weight of the edge
int u = p.second; // Vertex connected to the edge
if(visited[u] == true){
continue; // Skip if the vertex is already visited
}
res += wt; // Add the edge weight to the result
visited[u] = true; // Mark the vertex as visited
// Explore the adjacent vertices
for(auto v : adj[u]){
// v[0] represents the vertex and v[1] represents the edge weight
if(visited[v[0]] == false){
pq.push({v[1], v[0]}); // Add the adjacent edge to the priority queue
}
}
}
return res; // Return the sum of edge weights of the Minimum Spanning Tree
}
int main() {
vector<vector<int>> graph = {{0, 1, 5},
{1, 2, 3},
{0, 2, 1}};
cout << spanningTree(3, 3, graph) << endl;
return 0;
}
using namespace std;// Function to find sum of weights of edges of the Minimum Spanning Tree.int spanningTree(int V, int E, vector<vector<int>> &edges) { // Create an adjacency list representation of the graph vector<vector<int>> adj[V]; // Fill the adjacency list with edges and their weights for (int i = 0; i < E; i++) { int u = edges[i][0]; int v = edges[i][1]; int wt = edges[i][2]; adj[u].push_back({v, wt}); adj[v].push_back({u, wt}); } // Create a priority queue to store edges with their weights priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq; // Create a visited array to keep track of visited vertices vector<bool> visited(V, false); // Variable to store the result (sum of edge weights) int res = 0; // Start with vertex 0 pq.push({0, 0}); // Perform Prim's algorithm to find the Minimum Spanning Tree while(!pq.empty()){ auto p = pq.top(); pq.pop(); int wt = p.first; // Weight of the edge int u = p.second; // Vertex connected to the edge if(visited[u] == true){ continue; // Skip if the vertex is already visited } res += wt; // Add the edge weight to the result visited[u] = true; // Mark the vertex as visited // Explore the adjacent vertices for(auto v : adj[u]){ // v[0] represents the vertex and v[1] represents the edge weight if(visited[v[0]] == false){ pq.push({v[1], v[0]}); // Add the adjacent edge to the priority queue } } } return res; // Return the sum of edge weights of the Minimum Spanning Tree}int main() { vector<vector<int>> graph = {{0, 1, 5}, {1, 2, 3}, {0, 2, 1}}; cout << spanningTree(3, 3, graph) << endl; return 0;}// A Java program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency list
// representation of the graph
import java.io.*;
import java.util.*;
// Class to form pair
class Pair implements Comparable<Pair>
{
int v;
int wt;
Pair(int v,int wt)
{
this.v=v;
this.wt=wt;
}
public int compareTo(Pair that)
{
return this.wt-that.wt;
}
}
class GFG {
// Function of spanning tree
static int spanningTree(int V, int E, int edges[][])
{
ArrayList<ArrayList<Pair>> adj=new ArrayList<>();
for(int i=0;i<V;i++)
{
adj.add(new ArrayList<Pair>());
}
for(int i=0;i<edges.length;i++)
{
int u=edges[i][0];
int v=edges[i][1];
int wt=edges[i][2];
adj.get(u).add(new Pair(v,wt));
adj.get(v).add(new Pair(u,wt));
}
PriorityQueue<Pair> pq = new PriorityQueue<Pair>();
pq.add(new Pair(0,0));
int[] vis=new int[V];
int s=0;
while(!pq.isEmpty())
{
Pair node=pq.poll();
int v=node.v;
int wt=node.wt;
if(vis[v]==1)
continue;
s+=wt;
vis[v]=1;
for(Pair it:adj.get(v))
{
if(vis[it.v]==0)
{
pq.add(new Pair(it.v,it.wt));
}
}
}
return s;
}
// Driver code
public static void main (String[] args) {
int graph[][] = new int[][] {{0,1,5},
{1,2,3},
{0,2,1}};
// Function call
System.out.println(spanningTree(3,3,graph));
}
}
import heapq
def tree(V, E, edges):
# Create an adjacency list representation of the graph
adj = [[] for _ in range(V)]
# Fill the adjacency list with edges and their weights
for i in range(E):
u, v, wt = edges[i]
adj[u].append((v, wt))
adj[v].append((u, wt))
# Create a priority queue to store edges with their weights
pq = []
# Create a visited array to keep track of visited vertices
visited = [False] * V
# Variable to store the result (sum of edge weights)
res = 0
# Start with vertex 0
heapq.heappush(pq, (0, 0))
# Perform Prim's algorithm to find the Minimum Spanning Tree
while pq:
wt, u = heapq.heappop(pq)
if visited[u]:
continue
# Skip if the vertex is already visited
res += wt
# Add the edge weight to the result
visited[u] = True
# Mark the vertex as visited
# Explore the adjacent vertices
for v, weight in adj[u]:
if not visited[v]:
heapq.heappush(pq, (weight, v))
# Add the adjacent edge to the priority queue
return res
# Return the sum of edge weights of the Minimum Spanning Tree
if __name__ == "__main__":
graph = [[0, 1, 5],
[1, 2, 3],
[0, 2, 1]]
# Function call
print(tree(3, 3, graph))
using System;
using System.Collections.Generic;
public class MinimumSpanningTree
{
// Function to find sum of weights of edges of the Minimum Spanning Tree.
public static int SpanningTree(int V, int E, int[,] edges)
{
// Create an adjacency list representation of the graph
List<List<int[]>> adj = new List<List<int[]>>();
for (int i = 0; i < V; i++)
{
adj.Add(new List<int[]>());
}
// Fill the adjacency list with edges and their weights
for (int i = 0; i < E; i++)
{
int u = edges[i, 0];
int v = edges[i, 1];
int wt = edges[i, 2];
adj[u].Add(new int[] { v, wt });
adj[v].Add(new int[] { u, wt });
}
// Create a priority queue to store edges with their weights
PriorityQueue<(int, int)> pq = new PriorityQueue<(int, int)>();
// Create a visited array to keep track of visited vertices
bool[] visited = new bool[V];
// Variable to store the result (sum of edge weights)
int res = 0;
// Start with vertex 0
pq.Enqueue((0, 0));
// Perform Prim's algorithm to find the Minimum Spanning Tree
while (pq.Count > 0)
{
var p = pq.Dequeue();
int wt = p.Item1; // Weight of the edge
int u = p.Item2; // Vertex connected to the edge
if (visited[u])
{
continue; // Skip if the vertex is already visited
}
res += wt; // Add the edge weight to the result
visited[u] = true; // Mark the vertex as visited
// Explore the adjacent vertices
foreach (var v in adj[u])
{
// v[0] represents the vertex and v[1] represents the edge weight
if (!visited[v[0]])
{
pq.Enqueue((v[1], v[0])); // Add the adjacent edge to the priority queue
}
}
}
return res; // Return the sum of edge weights of the Minimum Spanning Tree
}
public static void Main()
{
int[,] graph = { { 0, 1, 5 }, { 1, 2, 3 }, { 0, 2, 1 } };
// Function call
Console.WriteLine(SpanningTree(3, 3, graph));
}
}
// PriorityQueue implementation for C#
public class PriorityQueue<T> where T : IComparable<T>
{
private List<T> heap = new List<T>();
public int Count => heap.Count;
public void Enqueue(T item)
{
heap.Add(item);
int i = heap.Count - 1;
while (i > 0)
{
int parent = (i - 1) / 2;
if (heap[parent].CompareTo(heap[i]) <= 0)
break;
Swap(parent, i);
i = parent;
}
}
public T Dequeue()
{
int lastIndex = heap.Count - 1;
T frontItem = heap[0];
heap[0] = heap[lastIndex];
heap.RemoveAt(lastIndex);
--lastIndex;
int parent = 0;
while (true)
{
int leftChild = parent * 2 + 1;
if (leftChild > lastIndex)
break;
int rightChild = leftChild + 1;
if (rightChild <= lastIndex && heap[leftChild].CompareTo(heap[rightChild]) > 0)
leftChild = rightChild;
if (heap[parent].CompareTo(heap[leftChild]) <= 0)
break;
Swap(parent, leftChild);
parent = leftChild;
}
return frontItem;
}
private void Swap(int i, int j)
{
T temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
}
class PriorityQueue {
constructor() {
this.heap = [];
}
enqueue(value) {
this.heap.push(value);
let i = this.heap.length - 1;
while (i > 0) {
let j = Math.floor((i - 1) / 2);
if (this.heap[i][0] >= this.heap[j][0]) {
break;
}
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
i = j;
}
}
dequeue() {
if (this.heap.length === 0) {
throw new Error("Queue is empty");
}
let i = this.heap.length - 1;
const result = this.heap[0];
this.heap[0] = this.heap[i];
this.heap.pop();
i--;
let j = 0;
while (true) {
const left = j * 2 + 1;
if (left > i) {
break;
}
const right = left + 1;
let k = left;
if (right <= i && this.heap[right][0] < this.heap[left][0]) {
k = right;
}
if (this.heap[j][0] <= this.heap[k][0]) {
break;
}
[this.heap[j], this.heap[k]] = [this.heap[k], this.heap[j]];
j = k;
}
return result;
}
get count() {
return this.heap.length;
}
}
function spanningTree(V, E, edges) {
// Create an adjacency list representation of the graph
const adj = new Array(V).fill(null).map(() => []);
// Fill the adjacency list with edges and their weights
for (let i = 0; i < E; i++) {
const [u, v, wt] = edges[i];
adj[u].push([v, wt]);
adj[v].push([u, wt]);
}
// Create a priority queue to store edges with their weights
const pq = new PriorityQueue();
// Create a visited array to keep track of visited vertices
const visited = new Array(V).fill(false);
// Variable to store the result (sum of edge weights)
let res = 0;
// Start with vertex 0
pq.enqueue([0, 0]);
// Perform Prim's algorithm to find the Minimum Spanning Tree
while (pq.count > 0) {
const p = pq.dequeue();
const wt = p[0]; // Weight of the edge
const u = p[1]; // Vertex connected to the edge
if (visited[u]) {
continue; // Skip if the vertex is already visited
}
res += wt; // Add the edge weight to the result
visited[u] = true; // Mark the vertex as visited
// Explore the adjacent vertices
for (const v of adj[u]) {
// v[0] represents the vertex and v[1] represents the edge weight
if (!visited[v[0]]) {
pq.enqueue([v[1], v[0]]); // Add the adjacent edge to the priority queue
}
}
}
return res; // Return the sum of edge weights of the Minimum Spanning Tree
}
// Example usage
const graph = [[0, 1, 5], [1, 2, 3], [0, 2, 1]];
// Function call
console.log(spanningTree(3, 3, graph));
Output
4
Time Complexity: O((E+V)*log(V)) where V is the number of vertex and E is the number of edges
Auxiliary Space: O(E+V) where V is the number of vertex and E is the number of edges
Advantages and Disadvantages of Prim's algorithm
Advantages:
- Prim's algorithm is guaranteed to find the MST in a connected, weighted graph.
- It has a time complexity of O((E+V)*log(V)) using a binary heap or Fibonacci heap, where E is the number of edges and V is the number of vertices.
- It is a relatively simple algorithm to understand and implement compared to some other MST algorithms.
Disadvantages:
- Like Kruskal's algorithm, Prim's algorithm can be slow on dense graphs with many edges, as it requires iterating over all edges at least once.
- Prim's algorithm relies on a priority queue, which can take up extra memory and slow down the algorithm on very large graphs.
- The choice of starting node can affect the MST output, which may not be desirable in some applications.
Problems based on Minimum Spanning Tree
- Kruskal's Algorithm for MST
- Minimum cost to connect all cities
- Minimum cost to provide water
- Second Best Minimum Spanning Tree
- Check if an edge is a part of any MST
- Minimize count of connections


Prim's Algorithm/Minimum Spanning Tree

