数学 すうがく 円 えん 英 えい circle )とは、平面 へいめん 次元 じげん ユークリッド空間 くうかん )上 じょう 定点 ていてん 距離 きょり 等 ひと 点 てん 集合 しゅうごう 曲線 きょくせん
その「定点 ていてん 円 えん 中心 ちゅうしん 円 えん 中心 ちゅうしん 円周 えんしゅう 上 じょう 点 てん 結 むす 線分 せんぶん 線分 せんぶん 長 なが 半径 はんけい [ 1] [ 2]
円 えん 定 てい 幅 はば 図形 ずけい 一 ひと
なお円 えん 囲 かこ 部分 ぶぶん 円 えん 内部 ないぶ 含 ふく 円 えん 場合 ばあい 厳密 げんみつ 必要 ひつよう 時 とき 境界 きょうかい 曲線 きょくせん 円周 えんしゅう 対 たい 内部 ないぶ 含 ふく 強調 きょうちょう 円 えん 板 ばん 三角形 さんかっけい 四角形 しかっけい 呼称 こしょう 統一 とういつ 円形 えんけい
習慣 しゅうかん 的 てき 円 えん 挙 あ 中心 ちゅうしん 名称 めいしょう 時 とき 呼 よ 多 おお 原点 げんてん 英語 えいご 英 えい Origin )」というのでその頭文字 かしらもじ 中心 ちゅうしん 点 てん 円 えん 円 えん 呼 よ 中心 ちゅうしん 英語 えいご 英 えい Center )」というので、円 えん 中心 ちゅうしん 文献 ぶんけん [ 3]
なお、数学 すうがく 以外 いがい 分野 ぶんや 曲線 きょくせん 近 ちか 卵 たまご 形 がた 総称 そうしょう 丸 まる 俗称 ぞくしょう 呼称 こしょう
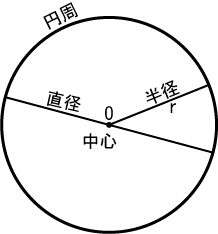
円 えん 中心 ちゅうしん 半径 はんけい 直径 ちょっけい 円周 えんしゅう
円周 えんしゅう 点 てん 交 まじ 直線 ちょくせん 割 わり 線 せん 交点 こうてん 点 てん 円周 えんしゅう 割 わり 線 せん 切 き 取 と 線分 せんぶん 弦 つる 弦 つる 呼 よ 特 とく 円 えん 中心 ちゅうしん 通 とお 割 わり 線 せん 中心 ちゅうしん 線 せん 中心 ちゅうしん 線 せん 円 えん 対称 たいしょう 軸 じく 円 えん 面積 めんせき 等分 とうぶん 円周 えんしゅう 中心 ちゅうしん 線 せん 切 き 取 と 弦 つる 長 なが 円 えん 直径 ちょっけい 直径 ちょっけい 半径 はんけい 倍 ばい 等 ひと 円周 えんしゅう 長 なが 円 えん 大 おお 円周 えんしゅう 長 なが 直径 ちょっけい 対 たい 比 ひ 値 ね 円 えん 依 よ 一定 いってい 円周 えんしゅう 率 りつ 特 とく 断 ことわ 限 かぎ 普通 ふつう 円周 えんしゅう 率 りつ π ぱい 表 あらわ 円 えん 半径 はんけい r (半径 はんけい 英語 えいご 頭文字 かしらもじ 由来 ゆらい 円周 えんしゅう 長 なが π ぱい r で表 あらわ 円 えん 面積 めんせき π ぱい r 2 で表 あらわ 同 おな 長 なが 周 しゅう 持 も 閉曲線 へいきょくせん 中 なか 面積 めんせき 最大 さいだい 等 とう 周 しゅう 問題 もんだい
中心 ちゅうしん 角 かく 円周 えんしゅう 角 かく 一方 いっぽう 円周 えんしゅう 割 わり 線 せん 部分 ぶぶん 分 わ 部分 ぶぶん 円弧 えんこ 単 たん 弧 こ
2つの弧 こ 長 なが 等 ひと 長 なが 方 ほう 弧 こ 優 ゆう 弧 こ 短 みじか 方 ほう 弧 こ 劣 れつ 弧 こ
2つの弧 こ 長 なが 等 ひと 弧 こ 半 はん 円周 えんしゅう 割 わり 線 せん 円 えん 中心 ちゅうしん 通 とお 中心 ちゅうしん 線 せん 円周 えんしゅう 上 じょう 点 てん 両 りょう 端 はし 弧 こ 弧 こ 呼 よ 記号 きごう 表記 ひょうき 記号 きごう 上 うえ 書 か 正 ただ 優 ゆう 弧 こ 劣 れつ 弧 こ 指定 してい 一方 いっぽう 特定 とくてい 場合 ばあい 弧 こ 上 じょう 点 てん 用 もち 弧 こ 表記 ひょうき
円 えん 周 しゅう 上 じょう 点 てん 半径 はんけい 弧 こ 囲 かこ 図形 ずけい 扇形 せんけい 扇形 せんけい 含 ふく 側 がわ 弧 こ 見込 みこ 中心 ちゅうしん 角 かく 一 ひと 円 えん 考 かんが 中心 ちゅうしん 角 かく 角 かく 見込 みこ 弧 こ 長 なが 比例 ひれい 同様 どうよう 中心 ちゅうしん 角 かく 角 かく 切 き 取 と 扇形 せんけい 面積 めんせき 比例 ひれい
弦 つる 弧 こ 囲 かこ 図形 ずけい 弓形 きゅうけい
弧 こ 対 たい 弧 こ 上 じょう 円 えん 周 しゅう 上 じょう 点 てん 取 と 弧 こ 対 たい 円周 えんしゅう 角 かく 弧 こ 対 たい 円周 えんしゅう 角 かく 点 てん 位置 いち 依 よ 一定 いってい 中心 ちゅうしん 角 かく 半分 はんぶん 等 ひと 円周 えんしゅう 角 かく 定理 ていり 特 とく 弧 こ 半 はん 円周 えんしゅう 弧 こ 対 たい 円周 えんしゅう 角 かく 直角 ちょっかく 直径 ちょっけい 見込 みこ 円周 えんしゅう 角 かく ターレスの定理 ていり )。
円 えん 内接 ないせつ 四角形 しかっけい 円 えん 周 しゅう 上 じょう 点 てん 四角形 しかっけい 円 えん 内接 ないせつ 内接 ないせつ 四角形 しかっけい 円 えん 四角形 しかっけい 外接 がいせつ 円 えん 四角形 しかっけい 円 えん 内接 ないせつ 四角形 しかっけい 対 たい 角 かく 和 わ 平 たいら 角 かく 等 ひと 内接 ないせつ 四角形 しかっけい 定理 ていり 円 えん 内接 ないせつ 四角形 しかっけい 外角 がいかく 大 おお 内 うち 対 たい 角 かく 大 おお 等 ひと 逆 ぎゃく 成立 せいりつ 四 よん 点 てん 共 ども 円 えん 定理 ていり 内接 ないせつ 四角形 しかっけい 定理 ていり
接 せっ 弦 つる 定理 ていり 円周 えんしゅう 直線 ちょくせん 共有 きょうゆう 点 てん 持 も 直線 ちょくせん 円 えん 接線 せっせん 共有 きょうゆう 点 てん 接点 せってん 円 えん 中心 ちゅうしん 接点 せってん 結 むす 半径 はんけい 接点 せってん 半径 はんけい 接線 せっせん 接点 せってん 直交 ちょっこう
円 えん 外部 がいぶ 点 てん 円 えん 接線 せっせん 描 えが 接点 せってん 線分 せんぶん 長 なが 接線 せっせん 長 なが 接線 せっせん 長 なが 等 ひと 円 えん 接線 せっせん 接点 せってん 通 とお 弦 つる 作 つく 角 かく 角 かく 中 なか 弧 こ 対 たい 円周 えんしゅう 角 かく 等 ひと 接 せっ 弦 つる 定理 ていり 下図 したず 接線 せっせん 接 せっ 弦 つる 定理 ていり 逆 ぎゃく 成立 せいりつ
円 えん 接吻 せっぷん 数 すう 完全 かんぜん 証明 しょうめい 1910年 ねん までできなかった。[要 よう 出典 しゅってん
半径 はんけい 異 こと 円 えん 位置 いち 関係 かんけい 2つの円 えん 円 えん 円 えん 位置 いち 関係 かんけい 次 つぎ 場合 ばあい 分 わ
円 えん 円 えん 内部 ないぶ 場合 ばあい 円 えん 円 えん 内包 ないほう 特 とく 中心 ちゅうしん 位置 いち 一致 いっち 円 えん 同心円 どうしんえん 呼 よ 円 えん 円 えん 周 しゅう 内部 ないぶ 点 てん 共有 きょうゆう 場合 ばあい 円 えん 円 えん 内接 ないせつ 2円 えん 異 こと 点 てん 共有 きょうゆう 場合 ばあい 円 えん 点 てん 交 まじ 点 てん 結 むす 弦 つる 共通 きょうつう 弦 つる
2円 えん 互 たが 周 しゅう 外部 がいぶ 点 てん 共有 きょうゆう 場合 ばあい 円 えん 円 えん 外接 がいせつ
2円 えん 互 たが 外部 がいぶ 共有 きょうゆう 点 てん 場合 ばあい 円 えん 離 はな 直線 ちょくせん 共通 きょうつう 弦 つる 正 せい 円 えん 包 つつ 外 そと 正 せい 円 えん 包 つつ 外 そと 正 せい 円 えん 共通 きょうつう 弦 つる 共通 きょうつう 弦 つる 交点 こうてん 共通 きょうつう 弦 つる 共通 きょうつう 弦 つる 交点 こうてん 時 とき 線上 せんじょう 三角形 さんかっけい 三 さん 辺 へん 位置 いち 長 なが 直径 ちょっけい 三 みっ 円 えん 生 しょう 本 ほん 共通 きょうつう 弦 つる 三角形 さんかっけい 本 ほん 頂 いただき 垂線 すいせん 既定 きてい 共通 きょうつう 弦 つる 持 も 円 えん 共通 きょうつう 弦 つる 一端 いったん 包 つつ 任意 にんい 別 べつ 円 えん 間 あいだ 本 ほん 共通 きょうつう 弦 つる 共通 きょうつう 弦 つる 交点 こうてん 共通 きょうつう 弦 つる 上 じょう 存在 そんざい 三角形 さんかっけい 三 さん 辺 へん 位置 いち 長 なが 直径 ちょっけい 三 みっ 円 えん 生 しょう 本 ほん 共通 きょうつう 弦 つる 三角形 さんかっけい 本 ほん 頂 いただき 垂線 すいせん 2つの円 えん 共通 きょうつう 接線 せっせん 共通 きょうつう 接線 せっせん
特 とく 円 えん 共通 きょうつう 接線 せっせん 関 かん 同 おな 側 がわ 共通 きょうつう 外接 がいせつ 線 せん 異 こと 側 がわ 共通 きょうつう 内接 ないせつ 線 せん
上記 じょうき 場合 ばあい 分 わ 描 えが 共通 きょうつう 接線 せっせん 個数 こすう
なし
共通 きょうつう 外接 がいせつ 線 せん 本 ほん 共通 きょうつう 外接 がいせつ 線 せん 本 ほん 共通 きょうつう 内接 ないせつ 線 せん 本 ほん 共通 きょうつう 外接 がいせつ 線 せん 本 ほん 計 けい 本 ほん 共通 きょうつう 内接 ないせつ 線 せん 本 ほん 共通 きょうつう 外接 がいせつ 線 せん 本 ほん 計 けい 本 ほん のいずれか。
半径 はんけい r ≔ 1中心 ちゅうしん (a , b ) ≔ (1.2, −0.5) の円 えん 解析 かいせき 幾何 きか 学 がく (a , b ) を中心 ちゅうしん 半径 はんけい r の円 えん
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
満 み 点 てん (x , y ) 全体 ぜんたい 軌跡 きせき 方程式 ほうていしき 円 えん 方程式 ほうていしき 言 い 中心 ちゅうしん (a , b ) と円上 えんじょう 任意 にんい 点 てん (x , y ) との二 に 点 てん 間 あいだ 距離 きょり r であるということを述 の 他 た 半径 はんけい 斜辺 しゃへん 直角 ちょっかく 三角形 さんかっけい ピタゴラスの定理 ていり を適用 てきよう 導出 どうしゅつ 直角 ちょっかく 挟 はさ 二 に 辺 へん 各 かく 座標 ざひょう 絶対 ぜったい 差 さ |x − a |, |y − b | を長 なが
中心 ちゅうしん 原点 げんてん 取 と 方程式 ほうていしき
x
2
+
y
2
=
r
2
{\textstyle x^{2}+y^{2}=r^{2}}
簡単 かんたん α あるふぁ β べーた γ がんま δ でるた 実数 じっすう α あるふぁ
a
:=
−
β べーた
α あるふぁ
,
b
:=
−
γ がんま
α あるふぁ
,
ρ ろー :=
β べーた
2
+
γ がんま
2
−
α あるふぁ δ でるた
α あるふぁ
2
{\displaystyle a:={\frac {-\beta }{\alpha }},\quad b:={\frac {-\gamma }{\alpha }},\quad \rho :={\frac {\beta ^{2}+\gamma ^{2}-\alpha \delta }{\alpha ^{2}}}}
書 か 上記 じょうき 方程式 ほうていしき
f
(
x
,
y
)
:=
α あるふぁ (
x
2
+
y
2
)
+
2
(
β べーた x
+
γ がんま y
)
+
δ でるた =
0
{\displaystyle f(x,y):=\alpha (x^{2}+y^{2})+2(\beta x+\gamma y)+\delta =0}
形 かたち 形 かたち x 2 , y 2 係数 けいすう 等 ひと xy の項 こう 持 も 方程式 ほうていしき 与 あた 以下 いか 何 いず 一 ひと 成 な 立 た
ρ ろー 方程式 ほうていしき 解 かい 実 み 点 てん 存在 そんざい 場合 ばあい 虚 きょ 円 えん [ 4] imaginary circle ) の方程式 ほうていしき 呼 よ ρ ろー 方程式 ほうていしき f (x , y ) = 0中心 ちゅうしん 一 いち 点 てん O ≔ (a , b )解 かい 点 てん 円 えん [ 5] point circle ) の方程式 ほうていしき 言 い ρ ろー f (x , y ) = 0O を中心 ちゅうしん 半径 はんけい r ≔ √ ρ ろー 円 えん 実 じつ 円 えん real circle ))の方程式 ほうていしき α あるふぁ f (x , y ) = 0直線 ちょくせん 方程式 ほうていしき a, b, ρ ろー は(射影 しゃえい 平面 へいめん 上 じょう 見 み 上 じょう 無限 むげん 大 だい 実 じつ 直線 ちょくせん 無限 むげん 遠 とお 点 てん 中心 ちゅうしん 半径 はんけい 無限 むげん 大 だい 円 えん 考 かんが 一般 いっぱん 化 か 円 えん (英語 えいご 版 ばん 項 こう 参照 さんしょう
表示 ひょうじ 中心 ちゅうしん 位置 いち c 円上 えんじょう 任意 にんい 点 てん 位置 いち x 二 に 点 てん 間 あいだ 距離 きょり ユークリッドノルム ‖ • ‖ ≔ ‖ • ‖2 : (x , y ) ↦ √ x 2 + y 2 用 もち ‖ x − c ‖ と書 か 半径 はんけい r の円 えん 方程式 ほうていしき
‖
x
−
c
‖
=
r
{\displaystyle \|\mathbf {x} -\mathbf {c} \|=r}
各 かく 点 てん 成分 せいぶん 表示 ひょうじ c ≔ (a , b ), x ≔ (x , y )与 あた
r
2
=
‖
x
−
c
‖
2
=
(
x
−
a
)
2
+
(
y
−
b
)
2
{\textstyle r^{2}=\|\mathbf {x} -\mathbf {c} \|^{2}=(x-a)^{2}+(y-b)^{2}}
上記 じょうき 円 えん 方程式 ほうていしき 媒介 ばいかい 変数 へんすう 表示 ひょうじ (a , b ) を中心 ちゅうしん 半径 はんけい r の円 えん 方程式 ほうていしき 正弦 せいげん 函数 かんすう 余弦 よげん 函数 かんすう 用 もち
{
x
=
a
+
r
cos
(
θ しーた )
y
=
b
+
r
sin
(
θ しーた )
(
0
≤
θ しーた <
2
π ぱい )
{\displaystyle {\begin{cases}x=a+r\cos(\theta )\\y=b+r\sin(\theta )\end{cases}}\qquad (0\leq \theta <2\pi )}
媒介 ばいかい 表示 ひょうじ 幾何 きか 学的 がくてき 媒介 ばいかい 変数 へんすう θ しーた (a , b ) から出 で (x , y ) を通 とお 半 はん 直線 ちょくせん 始 はじめ 線 せん x -軸 じく 正 せい 部分 ぶぶん 対 たい 角 かく 角度 かくど 解釈 かいしゃく 円 えん 別 べつ 媒介 ばいかい 表示 ひょうじ 半角 はんかく 正接 せいせつ 置換 ちかん
{
x
=
a
+
r
1
−
t
2
1
+
t
2
y
=
b
+
r
2
t
1
+
t
2
{\displaystyle {\begin{cases}x=a+r{\frac {1-t^{2}}{1+t^{2}}}\\y=b+r{\frac {2t}{1+t^{2}}}\end{cases}}}
与 あた 幾何 きか 学的 がくてき 媒介 ばいかい 変数 へんすう t の r に対 たい 比 ひ 中心 ちゅうしん 通 とお x -軸 じく 平行 へいこう 直線 ちょくせん 関 かん 立体 りったい 射影 しゃえい 解釈 かいしゃく 媒介 ばいかい 表示 ひょうじ t が任意 にんい 実数 じっすう 無限 むげん 遠 とお 点 てん 意味 いみ 持 も 一方 いっぽう 円 えん 最 もっと 下 した 一 いち 点 てん 表 あらわ 除 のぞ 三 さん 点 てん 標準 ひょうじゅん 形 がた 同 どう 一直線 いっちょくせん 上 じょう 三 さん 点 てん (xi , yi ) (i = 1, 2, 3三 さん 点 てん 通 とお 条件 じょうけん 満 み 円 えん 一 ひと 決 き 方程式 ほうていしき
(
x
−
x
1
)
(
x
−
x
2
)
+
(
y
−
y
1
)
(
y
−
y
2
)
(
y
−
y
1
)
(
x
−
x
2
)
−
(
y
−
y
2
)
(
x
−
x
1
)
=
(
x
3
−
x
1
)
(
x
3
−
x
2
)
+
(
y
3
−
y
1
)
(
y
3
−
y
2
)
(
y
3
−
y
1
)
(
x
3
−
x
2
)
−
(
y
3
−
y
2
)
(
x
3
−
x
1
)
{\displaystyle {\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}}
形 かたち 表 あらわ 行列 ぎょうれつ 式 しき 用 もち
|
x
2
+
y
2
x
y
1
x
1
2
+
y
1
2
x
1
y
1
1
x
2
2
+
y
2
2
x
2
y
2
1
x
3
2
+
y
3
2
x
3
y
3
1
|
=
0
{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0}
表 あらわ 射影 しゃえい 平面 へいめん 上 うえ 円 えん 方程式 ほうていしき 円上 えんじょう 任意 にんい 点 てん 斉 ひとし 次 じ 座標 ざひょう (英語 えいご 版 ばん 埋 う 込 こ (x , y ) ↦ [x : y : 1] のもとで) [x : y : z ] と書 か 一般 いっぱん 形 がた
x
2
+
y
2
−
2
a
x
z
−
2
b
y
z
+
c
z
2
=
0
{\displaystyle x^{2}+y^{2}-2axz-2byz+cz^{2}=0}
書 か
平面 へいめん 座標 ざひょう 系 けい 直交 ちょっこう 座標 ざひょう 系 けい 代 か 極座標 きょくざひょう 系 けい 用 もち 円 えん 方程式 ほうていしき 極座標 きょくざひょう 表示 ひょうじ 作 つく 円上 えんじょう 任意 にんい 点 てん 極座標 きょくざひょう (r , θ しーた とし、中心 ちゅうしん 極座標 きょくざひょう (r 0 , φ ふぁい (つまり、中心 ちゅうしん 原点 げんてん 距離 きょり r 0 φ ふぁい 原点 げんてん 中心 ちゅうしん 結 むす 半 はん 直線 ちょくせん x -軸 じく 正 せい 部分 ぶぶん 反 はん 時計 とけい 回 まわ 角 かく 半径 はんけい ρ ろー 円 えん 極 きょく 方程式 ほうていしき
r
2
−
2
r
r
0
cos
(
θ しーた −
φ ふぁい )
+
r
0
2
=
ρ ろー
2
{\displaystyle r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=\rho ^{2}}
書 か
中心 ちゅうしん 原点 げんてん 方程式 ほうていしき r = ρ ろー θ しーた 任意 にんい 単純 たんじゅん 形 かたち 極座標 きょくざひょう 系 けい 原点 げんてん 動 どう 径 みち 成分 せいぶん r = 0偏 へん 角 かく 成分 せいぶん θ しーた 任意 にんい 表 あらわ 原点 げんてん 円上 えんじょう 方程式 ほうていしき
r
=
2
ρ ろー cos
(
θ しーた −
φ ふぁい )
{\textstyle r=2\rho \cos(\theta -\varphi )}
簡約 かんやく 例 たと 半径 はんけい ρ ろー 中心 ちゅうしん 動 どう 径 みち 成分 せいぶん r 0 等 ひと 一般 いっぱん 場合 ばあい 方程式 ほうていしき r について解 と
r
=
r
0
cos
(
θ しーた −
ϕ
)
±
ρ ろー
2
−
r
0
2
sin
2
(
θ しーた −
φ ふぁい )
{\displaystyle r=r_{0}\cos(\theta -\phi )\pm {\sqrt {\rho ^{2}-r_{0}^{2}\sin ^{2}(\theta -\varphi )}}}
± の符号 ふごう 両方 りょうほう 取 と 半円 はんえん 記述 きじゅつ 場合 ばあい 注意 ちゅうい 複素数 ふくそすう 平面 へいめん 用 もち 平面 へいめん 上 じょう 円 えん 複素数 ふくそすう 用 もち 記述 きじゅつ 中心 ちゅうしん c で半径 はんけい r の円 えん 方程式 ほうていしき 複素数 ふくそすう 絶対 ぜったい 値 ち 用 もち
|
z
−
c
|
=
r
{\displaystyle |z-c|=r}
書 か 本質 ほんしつ 的 てき 円 えん 方程式 ほうていしき 同 おな 複素数 ふくそすう 平面 へいめん 複素数 ふくそすう 加法 かほう 実 じつ 数 すう 倍 ばい 成分 せいぶん 表示 ひょうじ 平面 へいめん 加法 かほう 実数 じっすう 倍 ばい 同一 どういつ 複素数 ふくそすう 絶対 ぜったい 値 ち 同一 どういつ 視 し 極 ごく 形式 けいしき 考 かんが |z − c | = r という条件 じょうけん z − c = r ⋅exp (iθ しーた )θ しーた 任意 にんい 同値 どうち 上記 じょうき 媒介 ばいかい 変数 へんすう 表示 ひょうじ 対応 たいおう
複素数 ふくそすう 積 せき 関 かん |z |2 = z ⋅z が成 な 立 た 注意 ちゅうい 方程式 ほうていしき 実数 じっすう p, q および複素数 ふくそすう g を用 もち
p
z
z
¯
+
g
z
+
g
z
¯
=
q
{\displaystyle pz{\overline {z}}+gz+{\overline {gz}}=q}
形 かたち 書 か
p
:=
1
,
g
:=
−
c
¯
,
q
:=
r
2
−
|
c
|
2
{\displaystyle p:=1,\,g:=-{\overline {c}},\,q:=r^{2}-|c|^{2}}
形 かたち 方程式 ほうていしき 円 えん 一般 いっぱん 一般 いっぱん 化 か 円 えん (英語 えいご 版 ばん 表 あらわ 一般 いっぱん 化 か 円 えん 通常 つうじょう 円 えん 直線 ちょくせん
極 ごく 方程式 ほうていしき 極 ごく 形式 けいしき 用 もち 複素数 ふくそすう 記述 きじゅつ
円上 えんじょう 点 てん P における接線 せっせん P を通 とお 直径 ちょっけい 垂直 すいちょく 円 えん 中心 ちゅうしん (a , b ) , 半径 はんけい r とし、P ≔ (x 1 , y 1 )垂直 すいちょく 条件 じょうけん 接線 せっせん 方程式 ほうていしき (x 1 − a )x + (y 1 – b )y = c の形 かたち (x 1 , y 1 ) を通 とお c は決定 けってい 接線 せっせん 方程式 ほうていしき
(
x
1
−
a
)
x
+
(
y
1
−
b
)
y
=
(
x
1
−
a
)
x
1
+
(
y
1
−
b
)
y
1
{\displaystyle (x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1}}
(
x
1
−
a
)
(
x
−
a
)
+
(
y
1
−
b
)
(
y
−
b
)
=
r
2
{\displaystyle (x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}}
形 かたち 書 か y 1 ≠ b 接線 せっせん 傾 かたむ
d
y
d
x
=
−
x
1
−
a
y
1
−
b
{\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}}
陰 かげ 函数 かんすう 微分 びぶん 法 ほう 用 もち 求 もと
中心 ちゅうしん 原点 げんてん 接線 せっせん 方程式 ほうていしき
x
1
x
+
y
1
y
=
r
2
{\textstyle x_{1}x+y_{1}y=r^{2}}
傾 かたむ
d
y
d
x
=
−
x
1
y
1
{\textstyle {\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}}
原点 げんてん 中心 ちゅうしん 円 えん 各 かく 点 てん 位置 いち (x , y ) と接 せっ (dx , dy ) が常 つね 直交 ちょっこう 内積 ないせき 零 れい
x
d
x
+
y
d
y
=
0
x{\mathit {dx}}+y{\mathit {dy}}=0
微分 びぶん 形 がた 円 えん 方程式 ほうていしき
三角形 さんかっけい 円 えん 関 かん 事柄 ことがら 扱 あつか 幾何 きか 学 がく 相似 そうじ 面積 めんせき 用 もち 円 えん 論 ろん 呼 よ 古来 こらい 非常 ひじょう 深 ふか 研究 けんきゅう 最 もっと 平面 へいめん 幾何 きか 学 がく 幾何 きか 学 がく 呼 よ
三角形 さんかっけい
それぞれの頂点 ちょうてん 対辺 たいへん 下 お 垂線 すいせん 足 あし
辺 あたり 中点 ちゅうてん 頂点 ちょうてん 垂心 すいしん 結 むす 線分 せんぶん 中点 ちゅうてん は全 すべ 同 どう 一 いち 円 えん 上 じょう 円 えん 九 きゅう 点 てん 円 えん 呼 よ
三角形 さんかっけい 頂点 ちょうてん 下 お 垂線 すいせん 足 あし 他 た 二 に 辺 へん 下 お 合計 ごうけい 個 こ 垂線 すいせん 足 あし 同 どう 一 いち 円周 えんしゅう 上 じょう 定理 ていり 中学 ちゅうがく 習 なら 円 えん 性質 せいしつ 証明 しょうめい 難解 なんかい
円 えん 内接 ないせつ 六角形 ろっかっけい 対辺 たいへん 延長線 えんちょうせん 交点 こうてん 一直線 いっちょくせん 上 じょう 拡張 かくちょう 二 に 次 じ 曲線 きょくせん 上 じょう 異 こと 点 てん 1 ~P6 を取 と 直線 ちょくせん 1 P2 と P4 P5 の交点 こうてん 1 、P2 P3 と P5 P6 の交点 こうてん 2 、P3 P4 と P6 P1 の交点 こうてん 3 は同 どう 一直線 いっちょくせん 上 じょう i 接線 せっせん j 接線 せっせん 交点 こうてん ij 直線 ちょくせん 12 R45 , R23 R56 , R34 R61 は1点 てん 交 まじ 一番 いちばん 初 はじ 円 えん 内接 ないせつ 六角形 ろっかっけい 証明 しょうめい 補助 ほじょ 円 えん 書 か 円 えん 性質 せいしつ 三角形 さんかっけい 相似 そうじ
三角形 さんかっけい 内接 ないせつ 円 えん 九 きゅう 点 てん 円 えん 内接 ないせつ
3 次元 じげん 空間 くうかん 点 てん 距離 きょり 一定 いってい 点 てん 集合 しゅうごう 球面 きゅうめん 内部 ないぶ 含 ふく 球面 きゅうめん 球 たま 一般 いっぱん n を自然 しぜん 数 すう n + 1 次元 じげん 空間 くうかん 点 てん 距離 きょり 一定 いってい 点 てん 集合 しゅうごう n 次元 じげん 球面 きゅうめん Sn と書 か 円 えん 次元 じげん 球面 きゅうめん
2つの点 てん 焦点 しょうてん 呼 よ 距離 きょり 和 わ 一定 いってい 点 てん 軌跡 きせき 楕円 だえん 楕円 だえん 一般 いっぱん 円 えん 潰 つぶ 形 かたち 楕円 だえん 特別 とくべつ 場合 ばあい 焦点 しょうてん 一 いち 点 てん 一致 いっち 場合 ばあい 円 えん 焦点 しょうてん 円 えん 中心 ちゅうしん 呼 よ 一般 いっぱん 楕円 だえん 円 えん 特 とく 明示 めいじ 円 えん 正 せい 円 えん 真 ま 円 えん 呼 よ
異 こと p に対 たい p -ノルム単位 たんい 円 えん 図示 ずし 「定点 ていてん 距離 きょり 一定 いってい 点 てん 全体 ぜんたい 成 な 集合 しゅうごう 円 えん 定義 ていぎ 定義 ていぎ 用 もち 距離 きょり 定義 ていぎ 変 か 異 こと 形状 けいじょう 円 えん 考 かんが p -ノルム(英語 えいご 版 ばん 誘導 ゆうどう 距離 きょり
‖
x
‖
p
:=
(
|
x
1
|
p
+
|
x
2
|
p
+
⋯
+
|
x
n
|
p
)
1
/
p
{\displaystyle \|x\|_{p}:=(|x_{1}|^{p}+|x_{2}|^{p}+\dotsb +|x_{n}|^{p})^{1/p}}
与 あた 幾何 きか 学 がく 通常 つうじょう ユークリッド距離 きょり :
‖
x
‖
2
=
|
x
1
|
2
+
|
x
2
|
2
+
⋯
+
|
x
n
|
2
{\displaystyle \|x\|_{2}={\sqrt {|x_{1}|^{2}+|x_{2}|^{2}+\dotsb +|x_{n}|^{2}}}}
p = 2場合 ばあい
タクシー幾何 きか 学 がく 用 もち マンハッタン距離 きょり (L 1 距離 きょり p = 1場合 ばあい 距離 きょり 関 かん 円 えん 円 えん 各 かく 辺 あたり 座標軸 ざひょうじく 45° ずれた正方形 せいほうけい 半径 はんけい r のタクシー円 えん 各 かく 辺 あたり 長 なが 距離 きょり 測 はか √ 2 r 距離 きょり 測 はか 2r である。よって、この幾何 きか 学 がく 円周 えんしゅう 率 りつ 半径 はんけい 対 たい 周 しゅう 長 ちょう 比 ひ 相当 そうとう 4 ということになる。タクシー幾何 きか 学 がく 単位 たんい 円 えん 半径 はんけい 円 えん 方程式 ほうていしき 直交 ちょっこう 座標 ざひょう 系 けい
|
x
|
+
|
y
|
=
1
{\textstyle |x|+|y|=1}
極座標 きょくざひょう 系 けい
r
=
1
|
sin
θ しーた
|
+
|
cos
θ しーた
|
{\textstyle r={\frac {1}{|\sin \theta |+|\cos \theta |}}}
書 か 中心 ちゅうしん フォンノイマン近傍 きんぼう (英語 えいご 版 ばん
平面 へいめん 上 じょう チェビシェフ距離 きょり (L ∞ 距離 きょり 対 たい 半径 はんけい r の円 えん 各 かく 辺 あたり 長 なが 2r の正方形 せいほうけい 各 かく 辺 あたり 座標軸 ざひょうじく 平行 へいこう 平面 へいめん 距離 きょり 平面 へいめん 距離 きょり 回転 かいてん 変換 へんかん 看做 みな L 1 L ∞ 間 あいだ 成 な 立 た 同値 どうち 性 せい 他 た 次元 じげん 一般 いっぱん 化 か
他 た 円 えん 特別 とくべつ 場合 ばあい 含 ふく 曲線 きょくせん 族 ぞく
編集 へんしゅう
円 えん 他 た 様々 さまざま 図形 ずけい 極限 きょくげん 場合 ばあい 見 み
デカルトの卵 たまご 形 がた 線 せん 焦点 しょうてん 呼 よ 定点 ていてん 距離 きょり 重 おも 付 つ 和 わ 一定 いってい 点 てん 全体 ぜんたい 成 な 軌跡 きせき 各 かく 距離 きょり 付 つ 重 おも 全 すべ 等 ひと 楕円 だえん 離 はなれ 心 しん 率 りつ 0 であるような楕円 だえん 円 えん 得 え 二 ふた 焦点 しょうてん 互 たが 重 かさ 極限 きょくげん 場合 ばあい 一致 いっち 焦点 しょうてん 得 え 円 えん 中心 ちゅうしん 重 おも 一方 いっぽう 0 として得 え 卵 たまご 形 がた 線 せん 円 えん 得 え
超 ちょう 楕円 だえん 適当 てきとう 正数 せいすう a, b > 0 と自然 しぜん 数 すう n に対 たい
|
x
a
|
n
+
|
y
b
|
n
=
1
{\textstyle \left|{\frac {x}{a}}\right|^{n}+\left|{\frac {y}{b}}\right|^{n}=1}
形 かたち 方程式 ほうていしき 持 も b = a 超 ちょう 円 えん 言 い 円 えん n = 2特別 とくべつ 超 ちょう 円 えん カッシーニの卵 たまご 形 がた 線 せん は二 ふた 定点 ていてん 距離 きょり 積 せき 一定 いってい 点 てん 全体 ぜんたい 軌跡 きせき 言 い 定点 ていてん 一致 いっち 円 えん 得 え 定 てい 幅 はば 曲線 きょくせん 幅 はば 図形 ずけい 幅 はば 挟 はさ 二 ふた 平行 へいこう 線 せん 各々 おのおの 図形 ずけい 境界 きょうかい 一 いち 点 てん 共有 きょうゆう 平行 へいこう 線 せん 間 あいだ 距離 きょり 定 さだ 平行 へいこう 線 せん 方向 ほうこう 方 かた 依 よ 一定 いってい 図形 ずけい 言 い 円 えん 単純 たんじゅん 定 てい 幅 はば 曲線 きょくせん 形 がた 例 れい
半径 はんけい R の円弧 えんこ 上 じょう 始点 してん 幅 はば w 1 、終点 しゅうてん 幅 はば w 2 の拡幅 かくふく 円弧 えんこ 長 なが 計算 けいさん
L
=
R
θ しーた
{\displaystyle L=R\theta }
k
=
w
2
−
w
1
L
{\displaystyle k={\frac {w_{2}-w_{1}}{L}}}
とすると、
d
L
=
(
R
+
w
1
+
k
R
θ しーた )
d
θ しーた
{\displaystyle dL=(R+w_{1}+kR\theta )d\theta }
L
w
=
(
R
+
w
1
)
θ しーた +
1
2
k
R
θ しーた
2
=
L
{
1
+
w
1
R
+
k
L
2
R
}
=
L
{
1
+
1
R
(
w
1
+
1
2
k
L
)
}
=
L
{
1
+
1
R
(
w
1
+
1
2
(
w
2
−
w
1
)
)
}
=
L
{
1
+
1
R
w
1
+
w
2
2
}
=
(
R
+
w
1
+
w
2
2
)
θ しーた
{\displaystyle {\begin{array}{rcl}Lw&=&\displaystyle (R+w_{1})\theta +{\frac {1}{2}}kR\theta ^{2}\\&=&\displaystyle L\left\{1+{\frac {w_{1}}{R}}+{\frac {kL}{2R}}\right\}\\&=&\displaystyle L\left\{1+{\frac {1}{R}}(w_{1}+{\frac {1}{2}}kL)\right\}\\&=&\displaystyle L\left\{1+{\frac {1}{R}}\left(w_{1}+{\frac {1}{2}}(w_{2}-w_{1})\right)\right\}\\&=&\displaystyle L\left\{1+{\frac {1}{R}}{\frac {w_{1}+w_{2}}{2}}\right\}\\&=&\displaystyle \left(R+{\frac {w_{1}+w_{2}}{2}}\right)\theta \end{array}}}
ゆえに、拡幅 かくふく 円 えん 長 なが 平均 へいきん 半径 はんけい 中心 ちゅうしん 角 かく
ウィキメディア・コモンズには、
円 えん 数学 すうがく に
関連 かんれん する
メディア および
カテゴリ があります。