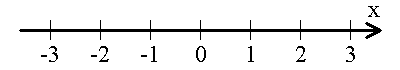直線 ちょくせん 無限 むげん 長 なが 物理 ぶつり 的 てき 表示 ひょうじ 不能 ふのう 為 ため 上記 じょうき 一部分 いちぶぶん 表示 ひょうじ 太 ふと 持 も 可視 かし 化 か 太 ふと 持 も 直線 ちょくせん 正確 せいかく 表示 ひょうじ 模 も 直線 ちょくせん 太 ふと 持 も 図形 ずけい 為 ため 厳密 げんみつ 正 ただ 表示 ひょうじ 場合 ばあい 視覚 しかく 確認 かくにん 不能 ふのう 画像 がぞう 直線 ちょくせん 太 ふと 持 も 模 も 画像 がぞう 線 せん 含 ふく 線分 せんぶん 直線 ちょくせん 太 ふと 持 も 幾何 きか 学 がく 的 てき 対象 たいしょう 曲線 きょくせん 一種 いっしゅ 上 うえ 点 てん 一様 いちよう 横 よこ 面 めん 無限 むげん 伸 の 端点 たんてん 持 も 線 せん 直線 ちょくせん 他 ほか 有限 ゆうげん 長 なが 両端 りょうたん 持 も 線分 せんぶん 一 ひと 端点 たんてん 始点 してん 無限 むげん 伸 の 半 はん 直線 ちょくせん 表記 ひょうき 場合 ばあい 可視 かし 化 か 太 ふと 持 も
ユークリッド の幾何 きか 学 がく 直線 ちょくせん 本質 ほんしつ 的 てき 無 む 定義 ていぎ 述語 じゅつご 直線 ちょくせん 何 なに 直接 ちょくせつ 定義 ていぎ 関係 かんけい 公理 こうり 公準 こうじゅん 満 み 理論 りろん 展開 てんかい 幾何 きか 学 がく 以下 いか
二 ふた 異 こと 点 てん 与 あた 通 とお 直線 ちょくせん 一 ひと 決 き 一 ひと 直線 ちょくせん 上 うえ 一 ひと 点 てん 与 あた 与 あた 点 てん 通 とお 与 あた 直線 ちょくせん 平行 へいこう 直線 ちょくせん 一 ひと 引 ひ また、このような公理 こうり 例 たと 以下 いか 導 みちび 二 ふた 異 こと 直線 ちょくせん 高々 たかだか 一 ひと 点 てん 共有 きょうゆう 二 ふた 異 こと 平面 へいめん 高々 たかだか 一 ひと 直線 ちょくせん 共有 きょうゆう
通常 つうじょう 直線 ちょくせん 線分 せんぶん 向 む 持 も 半 はん 直線 ちょくせん 向 む 持 も 扱 あつか 点 てん A と B を結 むす 線分 せんぶん AB と書 か AB = BA である。一方 いっぽう 向 む 付 づ 直線 ちょくせん 線分 せんぶん 向 む 持 も 半 はん 直線 ちょくせん 考 かんが 線分 せんぶん 始点 してん 終点 しゅうてん 区別 くべつ 線分 せんぶん 向 む 考 かんが 有向 ゆうこう 線分 せんぶん 呼 よ 有向 ゆうこう 線分 せんぶん AB ≠ BA と考 かんが
ユークリッド空間 くうかん 内 うち 有向 ゆうこう 線分 せんぶん 位置 いち 違 ちが 除 のぞ 類別 るいべつ 幾何 きか 学 がく 的 てき ベクトル (いわゆる矢印 やじるし 概念 がいねん 考 かんが 逆 ぎゃく 用 もち 空間 くうかん 中 なか 線分 せんぶん 直線 ちょくせん 定式 ていしき 化 か 後述 こうじゅつ
ユークリッド幾何 きか 学 がく 無 む 定義 ていぎ 述語 じゅつご 公理 こうり 構築 こうちく 幾何 きか 学 がく 直線 ちょくせん 本質 ほんしつ 持 も 曲 ま 空間 くうかん 幾何 きか 学 がく 非 ひ 幾何 きか 学 がく 直線 ちょくせん 測地 そくち 線 せん 幾何 きか 学 がく 中 なか 見 み 曲 ま 見 み
アフィン空間 くうかん (ベクトル)の理論 りろん 持 も 出 だ 次 つぎ 直線 ちょくせん 定義 ていぎ 出来 でき ユークリッド空間 くうかん E n 対 たい 任意 にんい 一 いち 点 てん P と 0 でない一 ひと ベクトル a が与 あた
L
=
{
P
+
λ らむだ
a
∣
λ らむだ ∈
R
}
{\displaystyle L=\{P+\lambda \mathbf {a} \mid \lambda \in \mathbb {R} \}}
で表 あらわ 集合 しゅうごう L を直線 ちょくせん 一般 いっぱん 空間 くうかん 拡張 かくちょう 定義 ていぎ 直線 ちょくせん 向 む 持 も a は直線 ちょくせん 方向 ほうこう 決 き P は直線 ちょくせん 上 じょう 点 てん 同 おな 直線 ちょくせん 与 あた 点 てん 組 くみ P , a は一 いち 通 とお 定義 ていぎ λ らむだ 動 うご 範囲 はんい 限定 げんてい 半 はん 直線 ちょくせん
L
+
=
{
P
+
λ らむだ
a
∣
λ らむだ ∈
R
≥
0
}
{\displaystyle L_{+}=\{P+\lambda \mathbf {a} \mid \lambda \in \mathbb {R} \geq 0\}}
や線分 せんぶん 記述 きじゅつ 同 おな 原点 げんてん 固定 こてい 点 てん 位置 いち 同一 どういつ 視 し 空間 くうかん 異 こと 点 てん A (a ), B (b ) ∈ E n 与 あた 時 とき
L
=
{
(
1
−
λ らむだ )
a
+
λ らむだ
b
∣
λ らむだ ∈
R
}
{\displaystyle L=\{(1-\lambda )\mathbf {a} +\lambda \mathbf {b} \mid \lambda \in \mathbb {R} \}}
なる集合 しゅうごう L は、A , B を含 ふく 直線 ちょくせん 向 む 考慮 こうりょ 方向 ほうこう b - a で、これは A から B へ向 む 引 ひ 定義 ていぎ λ らむだ 間 あいだ 限定 げんてい A から B までを結 むす 有向 ゆうこう 線分 せんぶん
A
B
→
=
{
(
1
−
λ らむだ )
a
+
λ らむだ
b
∣
0
≤
λ らむだ ≤
1
}
{\displaystyle {\overrightarrow {AB}}=\{(1-\lambda )\mathbf {a} +\lambda \mathbf {b} \mid 0\leq \lambda \leq 1\}}
が得 え
直線 ちょくせん 上 じょう 点 てん 実数 じっすう 対応 たいおう 数 かず 直線 ちょくせん 考 かんが 具体 ぐたい 的 てき 直線 ちょくせん 上 じょう 原点 げんてん O と単位 たんい 点 てん E を指定 してい 任意 にんい 実数 じっすう x に対 たい 直線 ちょくせん 上 じょう 一方 いっぽう 端点 たんてん 原点 げんてん 原点 げんてん 単位 たんい 点 てん 結 むす 有向 ゆうこう 線分 せんぶん 向 む 込 こ 線分 せんぶん 比 ひ x となるような線分 せんぶん 原点 げんてん 側 がわ 端点 たんてん x とを対応付 たいおうづ
しばしば、原点 げんてん 単位 たんい 点 てん 距離 きょり 整数 せいすう 倍 ばい 数 かず 目盛 めも 指 さ 数 かず 直線 ちょくせん 向 む 持 も 直線 ちょくせん 原点 げんてん 単位 たんい 点 てん 向 む 矢印 やじるし 記 しる 数 かず 直線 ちょくせん 次元 じげん ユークリッド空間 くうかん R に対 たい 座標 ざひょう 系 けい 捉 とら 出来 でき
原点 げんてん 単位 たんい 点 てん 目盛 めも 数 かず 直線 ちょくせん また、数 かず 直線 ちょくせん 用 もち 数 かず 和 わ 差 さ 図 ず 視覚 しかく 的 てき 与 あた 教育 きょういく 用 もち 例 たと 上 うえ 数 すう 直線 ちょくせん 足 た 算 ざん 和 わ 右 みぎ 進 すす 引 ひ 算 ざん 差 さ 左 ひだり 進 すす
1 + 2 は目盛 めも 目盛 めも 右 みぎ 進 すす
2 - 3 は目盛 めも 目盛 めも 左 ひだり 進 すす 互 たが 直交 ちょっこう 向 む 付 つ 数 かず 直線 ちょくせん ルネ・デカルト は絶対 ぜったい 的 てき 静止 せいし 座標 ざひょう 系 けい 定義 ていぎ 直交 ちょっこう 座標 ざひょう 系 けい 呼 よ
原点 げんてん 固定 こてい 原点 げんてん 始点 してん 半 はん 直線 ちょくせん 用 もち 極座標 きょくざひょう 系 けい 定義 ていぎ 半 はん 直線 ちょくせん 始 はじめ 線 せん 呼 よ
直交 ちょっこう 座標 ざひょう 系 けい 入 い 次元 じげん 空間 くうかん E 2 を考 かんが 時 とき 直線 ちょくせん 1次 じ 方程式 ほうていしき の形 かたち 与 あた
L
=
{
(
x
,
y
)
∣
a
x
+
b
y
=
c
}
{\displaystyle L=\{(x,y)\mid ax+by=c\}}
一般 いっぱん 次元 じげん 線型 せんけい 方程式 ほうていしき 系 けい 直線 ちょくせん 記述 きじゅつ 本質 ほんしつ 的 てき 記述 きじゅつ 同等 どうとう
幾何 きか 学 がく 的 てき 線分 せんぶん 点 てん 間 あいだ 結 むす 最短 さいたん 経路 けいろ
形式 けいしき 的 てき 点 てん 集合 しゅうごう V が与 あた 直積 ちょくせき 集合 しゅうごう V × V の元 もと 有向 ゆうこう 線分 せんぶん 同値 どうち 関係 かんけい 任意 にんい a , b ∈ V に対 たい a , b ) ~ (b , a ) と定 さだ 集合 しゅうごう E = V × V / ~ の元 もと 同値 どうち 類 るい a , b )] (a , b ∈ V , a ≠ b ) のこと(これをしばしば {a , b } と記 しる a と b を結 むす 線分 せんぶん 呼 よ
このように形式 けいしき 的 てき 線分 せんぶん 定義 ていぎ グラフ理論 りろん などにおける辺 あたり 線分 せんぶん 考 かんが
上 うえ 線分 せんぶん 線分 せんぶん 内分 ないぶん 点 てん 距離 きょり 距離 きょり 内分 ないぶん 点 てん
線分 せんぶん 延長線 えんちょうせん 上 じょう 線分 せんぶん 外 そと 分 ぶん 点 てん 距離 きょり 距離 きょり 線分 せんぶん 外 そと 分 ぶん 点 てん