Circles in Maths
A circle is a two-dimensional shape where all points on the circumference are the same distance from the center.
A circle consists of all points in a plane that are equidistant (at the same distance) from a fixed point called the centre. The distance from the centre to any point on the circle is called the radius. Its area is equal to pi times the square of its radius, or
π r2.
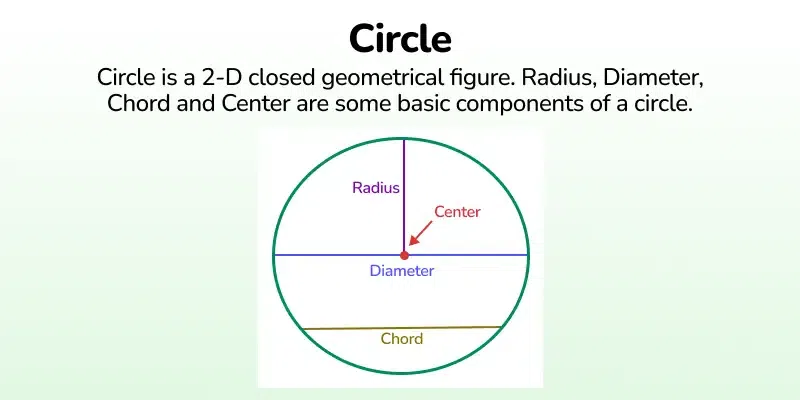
Diagram of a Circle
Circle Examples
Various objects that we observe in real life are circular in shape. Some examples of circular-shaped objects are Chapattis, Coins, Wheels, Rings, Buttons, CDs / DVDs, Bangles, Plates, etc.

How to Draw a Circle?
Drawing a circle is the most basic construction problem that is taught to students. Construction a circle requires some basic tools such as,
- Pencil
- Compass
- Scale or Ruler
To draw a circle follow the steps below,
- Step 1: Attach the pencil to the compass and make sure the tip of the compass and pencil are aligned properly.
- Step 2: Mark a point on the paper and call it the centre of the circle.
- Step 3: Measure the radius of the circle using the ruler and adjust the compass accordingly.
- Step 4: Draw the circle using the compass from the centre point marked in Step 2.
Interior and Exterior of Circle
If we draw a circle it divides the 2-D plane into three parts which are:
| Position | Description |
|---|---|
| Inside the Circle | A point whose distance from the circle’s center is less than the radius; is known as the interior point. |
| On the Circle | Points whose distance from the circle’s center is equal to the radius; these lie on the circumference. |
| Outside the Circle | Points whose distance from the circle’s center is greater than the radius; are known as exterior points. |
Parts of Circle
A circle has various parts and some of the important parts of the circle are:
Center of Circle: The Center of a circle is defined as the point from which any point on the circumference of the circle is at a fixed distance. The center of a circle is located inside the circle.
Radius of Circle: The Radius of the Circle is the distance between any point on the circumference of the circle and the fixed point called the center. The constant distance between any point on the circle and its center is called the radius. Radius = Diameter/2 , r = D/2
Diameter of Circle: A chord passing through the center of the circle is called the diameter of the circle. It is the largest chord of the circle and every diameter has an equivalent length. It is denoted by the letter ‘D’. Diameter = 2 × Radius , D = 2r

Chord of Circle: Any line which touches the circle at two points on its circumference is the chord of the circle. The diameter is also a chord of the circle. The longest chord of the circle is the diameter of the circle.
Tangent of Circle: A line that touches the circle only at one point on its circumference is called the tangent of the circle. It is always perpendicular to the radius of the circle at the point of tangency.
Secant of Circle: A line intersecting the circumference of the circle is called the secant on the circle. We also call it the extended chord.
Arc of a Circle
Any portion of the circumference of the circle is called the arc of the circle.
Segment in Circle: The chord divides the circle into two parts and each part is called the segment of the circle. There are two segments formed by a chord that is,
- Major Segment
- Minor Segment
Sector of a Circle: The area between two radii and the corresponding arc in a circle is called the sector of the circle. There are two types of sectors
- Major Sector
- Minor Sector
Properties of Circle
Some of the properties of the circle are :
- Circles with the same radii are called the congruent circle.
- Equal chords are equidistant from the center of the circle.
- Equidistant chords from the center of the circle are always equal.
- The perpendicular drawn from the center of the circle to the chord always bisects the chord.
- We can draw two tangents from an external point to a circle.
- Tangents drawn from the endpoints of the diameter are always parallel to each other.
Circle Formulas
There are various formulas related to the circle. Let the radius of the circle be ‘r’ then some of the important formulas related to the circle are:
| Formulas of Circle |
Expressions |
|---|---|
| Area of Circle | |
| Circumference of Circle | 2 |
| Length of Arc of Circle |
|
| Area of Sector of Circle |
( |
| Length of Chord |
2 r sin( |
| Area of Segment |
r2( |
Note: Value of
π is taken to be 3.14 or 22/7
Area of Circle Proof
We can easily prove the formula for the area of the circle using the area of the triangle formula. For this first, we have to draw various concentric circles inside the given circle. Then open all the concentric circles to form a right-angled triangle.

If the radius of the given circle is r, then the outer circle would form the base of the right triangle having length 2
The height of the triangle is ‘r’
The area of the right-angled triangle so formed is equal to the area of a circle.
Area of a Circle = Area of Triangle = (1/2) × base × height = (1/2) × 2
Therefore,
Area of Circle =
π r2
Types of Circles
Apart from our normal Circle, there are 5 other types of circles based on their shapes:
Semicircle: A semicircle is a two-dimensional geometric shape that is half of a complete circle. It is a shape formed by cutting a circle exactly in half.
Quarter Circle: A quarter circle, also known as a quadrant, is a shape formed by dividing a circle into four equal parts. It shares many similar properties with a semicircle.
Tangent Circles: These are two circles in the same plane that meet at exactly one point, without overlapping or intersecting further. This single point of contact is called the point of tangency. There are two main types of tangent circles:
- Internally Tangent Circles: These circles share the same interior space and touch each other inside that shared area.
- Externally Tangent Circles: These circles have separate interiors and touch each other outside those regions.
Concentric Circles: Concentric circles are two or more circles that have the same center point but different radii. Imagine dropping pebbles of different sizes into a still pond, creating ripples that share the same starting point but expand outwards at different rates.
Other Types of Circles
There are many other types of circles, some of which are:
- Circumcircle
- Incircle
- Excircle
- Fractal Circle
Circumcircle
A circumcircle refers to the unique circle that passes through all the vertices of a given polygon, such as a triangle, quadrilateral, or any other polygonal shape.
This circle’s center lies at the intersection of the perpendicular bisectors of the sides of the polygon, and its radius is the distance from the center to any of the vertices.
Inscribed circle or Incircle
An inscribed circle, also known as an incircle, is a circle that is tangent to all sides of a given polygon.
In the case of a triangle, the inscribed circle is the largest circle that fits snugly within the triangle, touching all three sides. The center of the incircle called the incenter, is the point of concurrency for the angle bisectors of the triangle, and its radius is known as the inradius.
Excircle or Escribed Circle
An excircle, or escribed circle, is a circle that lies outside a given polygon and is tangent to one of its sides and the extensions of the other two sides.
For example, in the context of a triangle, there are three excircles, each tangent to one side of the triangle and the extensions of the other two sides. The center of an excircle lies at the intersection of the external angle bisectors of the polygon, and its radius is known as the exradius.
Fractal Circles
Fractal circles are geometric figures that exhibit self-similarity and intricate patterns at multiple scales, characteristic of fractals.
They are created using recursive processes or algorithms that generate complex structures by repeatedly applying a set of rules.
Articles related to Circles in Math:
Solved Examples of Circles
Example 1: If the diameter of a circle is 142.8 mm, then what is the radius of the circle?
Solution:
Diameter = 142.8 mm
By Formula,
Diameter = 2 radiusRadius = (142.8 ÷ 2) = 71.4 mm
Thus, radius of circle is 71.4 mm
Example 2: Distance around a park is 21.98 yd. What is the radius of the park?
Solution:
Circumference of the Park = 21.98 yd
We know that,
Circumference = 2
π × Radius
Radius = Circumference / 2π Radius = 21.98 / 2×3.14 = 3.5
Thus, radius of circle is 3.5 yd
Example 3: The inner leveling circumference of a circular track is 440 m, and the track is 14 m wide. Calculate the cost of leveling the track at 25 rupees/m2.
Solution:
Let radius of inner circle be r m.
Now,Inner Circumference = 440 m
2
π r = 440
2 × 22/7 × r = 440
r = 440 × 744Inner Radius, r = 70
Width of track = 14 mOuter radius (R) = Inner Radius(r) + Width = (70 + 14) = 84 m
Area of Track =π (R2− r2)=
π (842 – 702)
= 22/7 × (7056 – 4900)
= 6776 m2Cost of leveling at 25 rupees per square meter = 6676 × 25 = 169400 Rupees
Thus, cost of leveling track is 169400 Rupees
Example 4: Find the length of the chord of a circle where the radius is 7 cm and the perpendicular distance from the chord to the center is 4 cm.
Solution:
Given,
Radius, r = 8 cm
Distance of Chord to Centre, d = 3 cmChord Length = 2√(r2 – d2)
= 2√(82 – 32)
= 2√(64 – 9)
= 2√55
= 2 × 7.416Chord length = 14.83 cm
Thus, length of chord is 14.83 cm
