Linear Equations in One Variable
Linear equation in one variable is the equation that is used for representing the conditions that are dependent on one variable. It is a linear equation i.e. the equation in which the degree of the equation is one, and it only has one variable.
A linear equation in one variable is a mathematical statement that involves a first-degree polynomial, and it can be expressed in the form: ax + b = c
Example: We can take any variable such as x, y, a, b, etc. Some examples of linear equations in one variable are,
- 2a + 3a = 20
- 5x + x = 12, etc.
The above equations are linear in one variable as they only have one variable and the highest degree of the variable is 1.




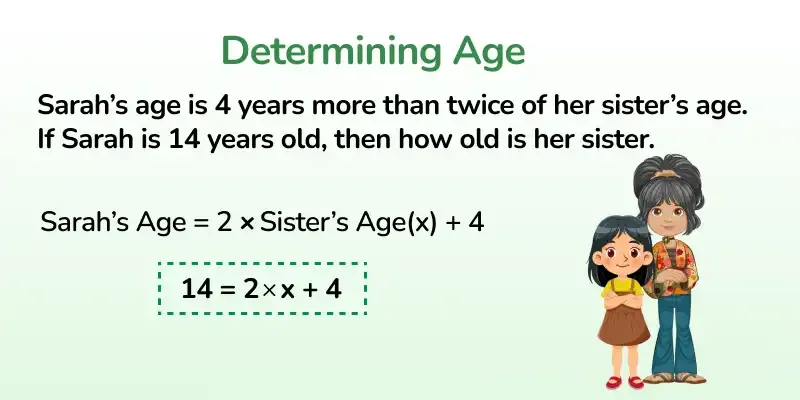
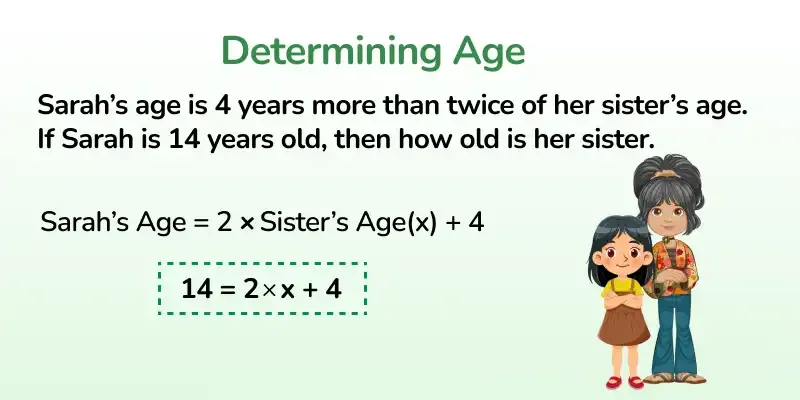


Graph of Linear Equation in One Variable
These linear equation can be easily represented on the graphs and they represent the straight line which can be horizontal to the coordinate axis or vertical to the coordinate axis.
We represent the mathematical condition using these equations as the condition "a number which is 5 less than twice of itself" is represented by the linear equation,
x = 2x - 5 , Where x is the unknown number.

In the above equation there is only one variable (x) and the degree of the variable is one thus, it is a linear equation in one variable.
Standard Form of Linear Equation in One Variable
A linear equation in one variable can be expressed in the standard form
ax+b = 0
where x is the variable and a and b are the constants involved. These constants (a and b) are non-zero real numbers. These equations have only one possible solution for the value of the variable.
Solving Linear Equations in One Variable
Linear Equations in One Variable can easily be solved by following the steps discussed below,
- Step 1: Write the given equation in standard form and if a or b is a fraction then take the LCM of the fraction to make them integers.
- Step 2: The constants are then taken to the right side of the equation.
- Step 3: All the variables and the constant terms are then simplified to form one single variable term and one single constant.
- Step 4: The coefficient of the variable is made 1 by dividing both sides with a suitable constant to get the final result.
Let's understand the above steps with the help of the following example.
Examples on Linear Equation in One Variable
Solve the following linear equation in one variable.
Example: Solve 3x + 1/2 = (1/2)x - 13/2
Solution:
Step 1: Arranging in standard form and taking LCM
3x - (1/2)x + 1/2 + 13/2 = 0
⇒ (6x - x + 1 + 13)/2 = 0
⇒ 6x - x + 1 + 13 = 0
Step 2: Transposing the constant to the right-hand side
6x - x = -1 - 13
Step 3: Simplification
5x = -14
Step 4: Make coefficient of x to 1
Dividing both sides by 5 we get,
5x/5 = -14/5
x = -14/5
This is the required solution.
Linear Equations and Non-Linear Equations
As we have already learned that linear equations are the equations with the highest degree of "one" and they represent a straight line on the coordinate plane. Examples of linear equations are,
- 3x = 5
- x + y = 12
- 3x - 4y = 11, etc.
All these linear equations represent the straight line in coordinate planes.
All the equations which have a degree greater than one are called non-linear equations they represent curves in the coordinate plane. Various types of non-linear equations represent various types of curves in the 2-D plane. Some of the common curves which we study are,
Circle: x2 + y2 = 49, this equation represents a circle in an x-y coordinate plane with a center at (0, 0) and a radius of 7 units.
Similarly,
- y2 = 16x represents a parabola.
- x2/16 + y2/25 = 1 represents an ellipse.
- x2/16 - y2/25 = 1 represents a hyperbola.
All these equations discussed above are non-linear equations.
Difference between Linear Equations and Non-Linear Equations
The key differences between Linear Equations and Non-Linear Equations are:
| Feature | Linear Equations | Non-Linear Equations |
|---|---|---|
| Definition | Equations of the form ax + by = c, where a, b, and c are constants, and x and y are variables raised to the power of 1. | Equations where the highest power of the variables is greater than 1, or variables are multiplied together. |
| Graph | Represented by straight lines. | Represented by curves or irregular shapes. |
| Solution(s) | Always forms a straight line when graphed. | Can form curves, loops, or irregular shapes when graphed. |
| Number of Solutions | Always one solution (if the lines intersect). | Can have multiple solutions or none. |
| Solution Method | Solvable using algebraic methods like substitution, elimination, or graphing. | Often require numerical or iterative methods for solutions. |
Must Read
- Solve Linear Equations with Variables on Both Sides
- Linear Equations Formula
- Linear Equation in Two Variable
Also Check
- Linear Equations in One Variable Class 8 Notes
- Linear Equations in One Variable Class 8 NCERT Solutions
Linear Equation in One Variable Examples
Example 1: Solve for y, 8y - 4 = 0
Solution:
Solving for value of y,
Adding 4 to both sides of the equation ,
8y -4 + 4 = 4
8y = 4Dividing both sides of equation by 8
y = 4/8Simplifying the equation ,
y = 1/2
Example 2: Solve the equation in x, 3x +10 = 55
Solution:
Taking constants to RHS,
3x = 45
x = 15
Example 3: Solve the equation in x, 4/x5 -5 = 15
Solution:
4/x5 -5 = 15
⇒ 4x/5 = 15 + 5
⇒ 4x/5 = 20
⇒ x = 20×5/4
⇒ x = 25
Example 4: The age of Ravi is twice the age of his sister Kiran if the sum of their age is 24 find their individual age.
Solution:
Let the age of Kiran is x, then the age of Ravi is 2x
Given, the sum of their ages is 24
x + 2x = 24
⇒ 3x = 24
⇒ x = 8Thus, the age of Kiran = x = 8 years
Age of Ravi = 2x = 2×8 = 16 years
Example 5: Akshay earns three times more than Abhay and if the difference in their salaries is Rs 5000 find their individual salaries.
Solution:
Let the salary of Abhay be x, then the salary of Akshay is 3x
Given, the difference in their salaries is Rs 5000
3x - x = 5000
⇒ 2x = 5000
⇒ x = 2500Thus, the salary of Abhay = x = Rs 2500
The salary of Akshay = 3x = 3×2500 = Rs 7500
