Area of Parallelogram | Definition, Formulas & Examples

A parallelogram is a four-sided polygon (quadrilateral) where opposite sides are parallel and equal in length. In a parallelogram, the opposite angles are also equal, and the diagonals bisect each other (they cut each other into two equal parts).

The area of a Parallelogram is the space or the region enclosed by the boundary of the parallelogram in a two-dimensional space. It is calculated by multiplying the base of the parallelogram by its height.

Area of Parallelogram Formula

The area of a Parallelogram can be determined by multiplying its base by its altitude. Thus, the following formula can be used to determine a parallelogram's area,

Area of Parallelogram = Base × Height
A = b × h

For any parallelogram of base(b) and height(h) whose image is shown below, its area is bh units.

Example: Find the area of a parallelogram whose base is 12 cm and height is 8 cm.

Given,
Base (b) = 12 cm
Height (h) = 8 cm

The formula to calculate the area of a parallelogram is,

A = b × h 
A = 12 × 8 
A = 96 cm²

Area of Parallelogram using Side Lengths

Area of a Parallelogram can be calculated by using the length of sides and adjacent angles if the height is not given. Mathematically it is written as,

Area of Parallelogram = ab sin (θしーた)

For any parallelogram of sides 'a' and 'b' and angle between them is 'θしーた' whose image is shown below, its area is ab sin (θしーた) units.

Example: If the angle between two sides of a parallelogram is 30 degrees and the length of its adjacent sides are 5 cm and 6 cm. Determine the area of parallelogram.

Given,
Length of One side (a) = 5 cm
Length of Other side (b) = 4 cm

Angle between two adjacent sides (θしーた) = 30 degrees

Formula to calculate Area of a Parallelogram is,
A = ab sin (θしーた)
A = 5 × 4 × sin (30)
A = 10 cm²

Area of Parallelogram using Diagonals

A parallelogram consists of two diagonals that intersect each other at a specific angle meeting at a particular point. The area of a parallelogram can be calculated by using the length of its diagonals.

Formula for the area of parallelogram by using the length of diagonals is given by,

Area of Parallelogram = 1/2 × d₁ × d₂ sin (x)

For any parallelogram of diagonals 'd₁' and 'd₂' and angle between them is 'x' whose image is shown below, its area is 1/2 × d₁ × d₂ sin (x) units.

Example: Determine the area of parallelogram, when the angle between two intersecting diagonals of a parallelogram is 90 degrees and the length of its diagonals are 2 cm and 6 cm.

Given,
Length of One Diagonal (d₁) = 2 cm
Length of Other Diagonal (d₂) = 6 cm

Angle between two intersecting diagonals (x) = 90 degrees

Formula to calculate Area of a Parallelogram is,

A = 1/2 × d₁ × d₂ sin (x)
A = 1/2 × 2 × 6 × sin (90)
A = 6 cm²

Formula Table for the Area of Parallelogram

Area of Parallelogram in Vector form

Area of Parallelogram in vector form involves using vectors to express the sides of the parallelogram and then calculating the cross-product of those vectors. The magnitude of the cross-product yields the area of the parallelogram.

Let's considering a parallelogram PQRS, with adjacent sides [Tex]\vec a[/Tex] and [Tex]\vec b[/Tex] and the diagonals are [Tex]\vec {d_1}[/Tex]and [Tex]\vec {d_2}[/Tex]

Now, Area of Parallelogram in vector form is given using adjacent sides [Tex]\vec a[/Tex] and [Tex]\vec b[/Tex] as, 

[Tex]A = |\vec a \times \vec b| [/Tex]

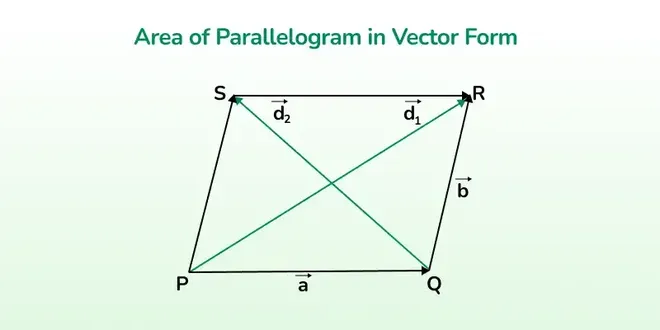
Using the Parallelogram Law of Vector Addition

• [Tex]\vec a + \vec b = \vec d_1[/Tex]
• [Tex]\vec b -\vec a = \vec d_2[/Tex]

Now,

[Tex]\begin{aligned}\vec d_1 \times \vec d_2 &= (\vec a + \vec b)(\vec b - \vec a)\\&=\vec a \times(\vec b - \vec a)+\vec b\times (\vec b - \vec a)\\&=\vec a \times \vec b - \vec a\times \vec a +\vec b\times \vec b - \vec b \times \vec a)\end{aligned}[/Tex]

But, [Tex]\vec a \times \vec a = 0[/Tex], [Tex]\vec b \times \vec b = 0[/Tex] and [Tex]\vec a \times \vec b = - \vec b \times \vec a [/Tex]

Therefore,

[Tex]\begin{aligned}\vec d_1 \times \vec d_2 &=\vec a \times \vec b - 0 +0 - \vec b \times \vec a)\\&=\vec a \times \vec b - (-(\vec a \times \vec b))\\&=2(\vec a\times \vec b)\end{aligned} [/Tex]

[Tex]|\vec a + \vec b| = \dfrac{1}{2} |(\vec d_1\times \vec d_2)| [/Tex]

The Magnitude of the cross product of the diagonals relates to the area as:

[Tex]A = \frac{1}{2}|\vec{d_1} \times \vec{d_2}|[/Tex]

Example: Find the area of a parallelogram whose adjacent sides are vectors. A = 2i + 5j and B = 7i - j

Area of Parallelogram = |A × B|

Area = [Tex]\begin{vmatrix} i& j\\ 2& 5\\ 7& -1\end{vmatrix}[/Tex]

Area = (2)(-1) -5(5)(7) = -2 -35 = |-37|

Area of Prarallelogram is 37 units

Area of Parallelogram Solved Examples

Various examples related to Area of Parallelogram are,

Example 1: Find area of a parallelogram whose base is 10 cm and height is 8 cm.

Solution:

Given,
Base (b) = 10 cm
Height (h) = 8 cm

We have,

A = b × h = 10 × 8 = 80 cm²

Example 2: Find the area of a parallelogram whose base is 5 cm and height is 4 cm. 

Solution:

Given,
Base (b) = 5 cm 
Height (h) = 4 cm

Area(A) = b × h 
A = 5 × 4 = 20 cm²

Example 3: Determine the area of the parallelogram, when the angle between two intersecting diagonals of a parallelogram is 90 degrees and the length of its adjacent sides are 4 cm and 8 cm.

Solution:

Given,
Length of One Diagonal (d₁) = 4 cm
Length of Other Diagonal (d₂) = 8 cm

Angle between two intersecting diagonals (x) = 90 degrees

Formula to calculate the area of a parallelogram is,
A = 1/2 × d₁ × d₂ sin (x)
A = 1/2 × 4 × 8 × sin (90)
A = 16 cm²

Example 4: If the angle between two sides of a parallelogram is 60 degrees and the length of its adjacent sides is 3 cm and 6 cm. Determine the area of the parallelogram.

Solution:

Given,
Length of One side (a) = 3 cm
Length of Other side (b) = 6 cm

Angle between two adjacent sides (θしーた) = 60 degrees

Formula to calculate Area of a Parallelogram is,

A = ab sin (θしーた)
A = 3 × 6 × sin (60)
A = 15.6 cm²

Example 5: Find the area of a parallelogram whose adjacent sides are 4 cm and 3 cm and the angle between these sides is 90°.

Solution:

Let lengths of sides by a and b with values 4 cm and 3 cm respectively.

Angle between sides 90°

Area = ab sinθしーた

A = 4 × 3 sin 90°

A = 12 cm²

Practice Questions on Area of Parallelogram

Some practice questions on Area of parallelogram are,

Question 1. Find the area of a parallelogram whose adjacent sides are 12 cm and 14 cm and the angle between these sides is 60°.

Question 2. If angle between two sides of a parallelogram is 30 degrees and the length of its adjacent sides is 3 cm and 6 cm. Find its Area.

Question 3. If base and height of a parallelogram is 4 cm and 8 cm respectively, find its area.

Question 4. What is area of a parallelogram whose breadth is 11 cm and height is 18 cm.

Answer Key

Answer 1: Area of a parallelogram with adjacent sides 12 cm and 14 cm, and an angle of 60°: 145.49 cm²
Answer 2: Area of a parallelogram with adjacent sides 3 cm and 6 cm, and an angle of 30°: 9 cm²
Answer 3: Area of a parallelogram with base 4 cm and height 8 cm: 32 cm²
Answer 4: Area of a parallelogram with breadth 11 cm and height 18 cm: 198 cm²