Area of a Triangle | Formula and Examples
The area of the triangle is a basic geometric concept that calculates the measure of the space enclosed by the three sides of the triangle. The formulas to find the area of a triangle include the base-height formula, Heron's formula, and trigonometric methods.
The area of triangle is generally calculated with the help of its base and height. To find the Area of a triangle A with base b and height h, We use the formula:

The most general formula for the area of a triangle is given by half the product of its base and height. It applies to all types of triangles, whether it is equilateral, isosceles triangles, or scalene triangles.
Types of Triangle
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
Area of Triangle Formula
The formula for the area of a triangle depends on the dimensions of the triangle. The following table consists of the area of triangle formulas used in different contexts:
| Triangle Type | Formula |
|---|---|
| Right-Angled Triangle | ½ × base × height |
| Equilateral Triangle | (√3)/4 × side2 |
| Isosceles Triangle | ¼ × b√(4a2 - b2) |
| Using Heron's Formula | √{s(s - a)(s - b)(s - c)} ,where s = ½ (a+b+c) |
| When Two Sides and Included Angle (SAS) are given | ½ × side 1 × side 2 × sin( , where |
| In Coordinate Geometry | ½ |x1(y2 - y3 ) + x2(y3 - y1) + x3(y1 - y2)| , where (x1, y1), (x2, y2) and (x3, y3) are the coordinates of triangle. |
Area of Right Angled Triangle
A triangle that contains a right angle is considered a right-angled triangle.
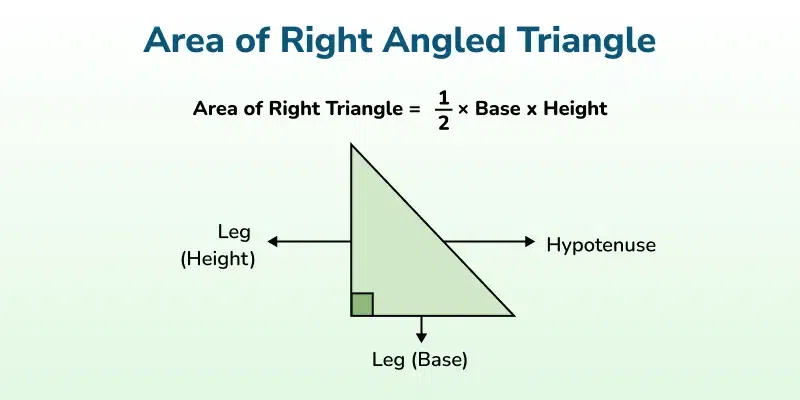
Area of Right Angled Triangle Formula :
A = 1/2 × a × c
where,
a is the base of the triangle
c is the height of the triangle
Example: Find the area of a right-angled triangle having base a = 5 cm and height c = 3 cm.
Solution:
Given:Base of the triangle (a) = 5 cm
Height of the triangle (c) = 3 cmWe have,
Area(A) = 1/2 × a × c
= 1/2 × 5 × 3
= 7.5 cm2
Read More: Right Angled Triangle
Area of Equilateral Triangle
An equilateral triangle has all three sides equal and all three angles equal, measuring 60 degrees.
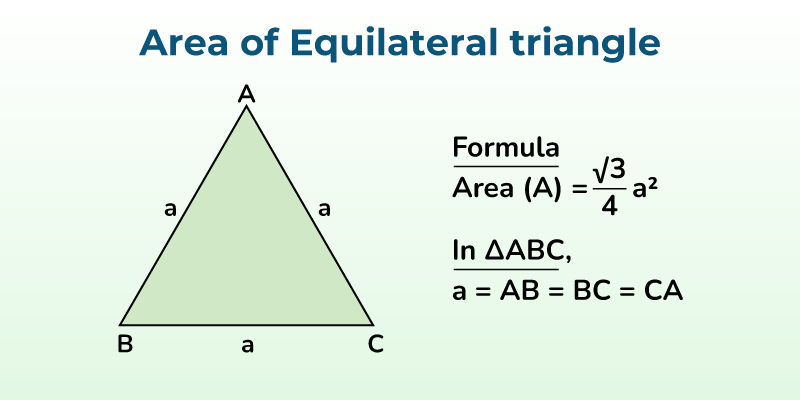
Area of Equilateral Triangle Formula :
A = (√3)/4 × side2
= (√3)/4 × a2
Example: Find the area of an equilateral triangle having side a = 6 cm.
Solution:
Given,side of the triangle (a) = 6 cm
Area(A) = (√3)/4 × a2
= (√3)/4 × 62
= 9√3 cm2
Read More :
Area of Isosceles Triangle
An isosceles triangle has two equal sides and the angles opposite these equal sides are also equal.
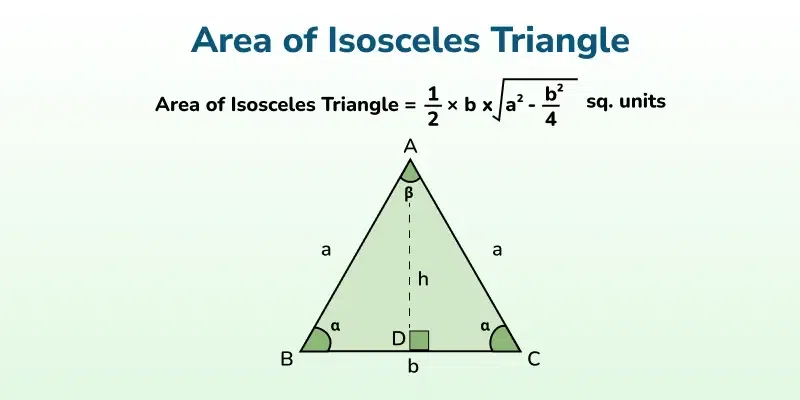
Area of Isosceles Triangle Formula :
A = ½ × b√(a2 - (b2/4))
Where,
a = both the equal sides and b = the third unequal side.
Example: What is the area of an isosceles triangle with sides 5 cm, 5 cm, and 6 cm?
Solution:
Using the Formula: A = ½ × b√(a2 - (b2/4))
- a = 5 cm (the equal sides),
- b = 6 cm (the base).
Learn More :
Area of Scalene Triangle
A scalene triangle has all three sides of different lengths, and all three angles are different as well.
Key Features:
- No sides are congruent (all sides have different lengths).
- No angles are equal.
- It has no symmetry.
Example: A triangle with sides of 3 cm, 5 cm, and 7 cm is a scalene triangle.
Area of Triangle By Heron's Formula
The area of a triangle with 3 sides given can be found using Heron's Formula. This formula is useful when the height is not given.
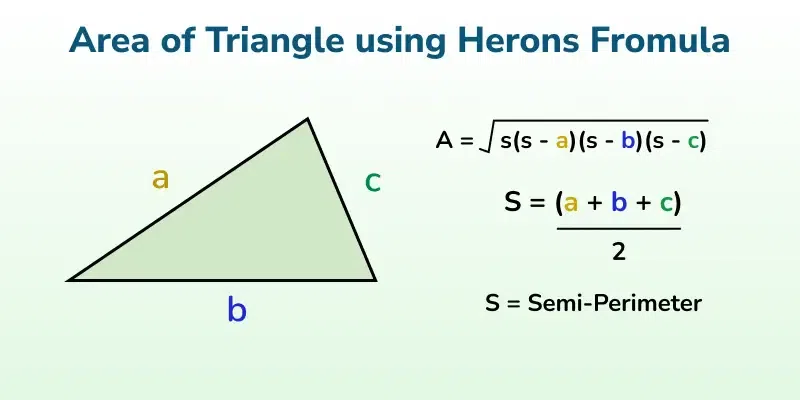
Heron's Formula is given by,
Area of Triangle = √{s(s - a)(s - b)(s - c)}where, a, b, and c are sides of the given triangle
and s = ½ (a+b+c) is the semi perimeter.
Example: What is the area of a triangle with sides of 3 cm, 4 cm, and 5 cm?
Solution:
Using Heron's formula,
s = (a+b+c)/2
= (3+4+5)/2
= 12/2 = 6Area = √{ s(s-a)(s-b)(s-c)}
= √{ 6(6-3)(6-4)(6-5)}
= √(6 × 3 × 2 × 1) = √(36
= 6 cm2
Learn More: Heron's Formula
Area of Triangle With Two Sides and Included Angle (SAS)
Area of SAS Triangle is obtained by using the concept of trigonometry.
Let us assume ABC is right angled triangle and AD is perpendicular to BC.

In the above figure,
Sin B = AD/AB
⇒ AD = AB Sin B = c Sin B
⇒ Area of Triangle ABC = 1/2 ⨯ Base ⨯ Height
⇒ Area of Triangle ABC = 1/2 ⨯ BC ⨯ AD
⇒ Area of Triangle ABC = 1/2 ⨯ a ⨯ c Sin B
= 1/2 ⨯ BC ⨯ AD
Thus,
Area of Triangle = 1/2 ac Sin B
Similarly, we can find that,
Area of Triangle = 1/2 bc Sin A
Area of Triangle = 1/2 ab Sin C
We conclude that the area of a triangle using trigonometry is given as, half the product of two sides and sine of the included angle.
Area of Triangle in Coordinate Geometry
In Coordinate Geometry, if the coordinates of triangle ABC are given as A(x1, y1), B(x2, y2), and C(x3, y3), then its Area is given by the following formula :
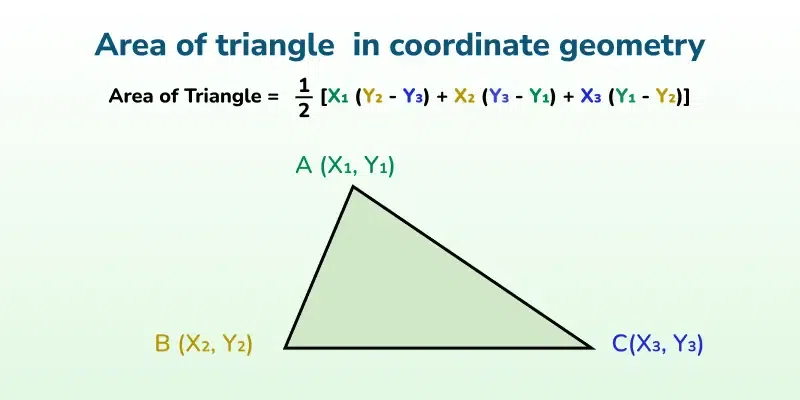
⇒ Area of △ABC = ½[x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)]
Articles related to the Area:
