Mid Point Theorem

The Midpoint Theorem is a fundamental concept in geometry that simplifies solving problems involving triangles. It establishes a relationship between the midpoints of two sides of a triangle and the third side. This theorem is especially useful in coordinate geometry and in proving other mathematical theorems.

The midpoint theorem states that if a segment is formed by connecting the midpoints of two of the sides of a triangle, then that segment must be parallel to the third side and equal to third side of the triangle

In other words, if you take any triangle and connect the midpoints of two sides, the line formed will be parallel to the third side and exactly half as long.

For example, consider a triangle, ΔでるたABC. Let D and E be the midpoints of AB and AC respectively, now join DE. Then the midpoint theorem states that DE is parallel to BC and equal to half of BC.

Mid-Point Theorem Proof

• Given: A triangle ABC in which D is the mid-point of AB and E is the mid-point of AC.
• To Prove: DE ∥ BC and DE = 1/2(BC)
• Construction: Extend the line segment joining points D and E to F such that DE = EF, and join CF.

Proof:

In ∆AED and ∆CEF:

• DE = EF (construction)
• ∠1 = ∠2 (vertically opposite angles)
• AE = CE (E is the mid-point)

By SAS criterion, △AED ≅ △CEF.

Therefore, ∠3 =∠4 (by CPCT)

But these are alternate interior angles, so AB ∥ CF

• AD = CF  (CPCT)
• But AD = DB (D is the mid-point), so BD = CF

In Quadilateral BCFD:

• BD∥ CF (since AB ∥ CF)
• BD = CF

BCFD is a parallelogram as one pair of opposite sides is parallel and equal.

Therefore, 
DF∥ BC (opposite sides of parallelogram)
DF = BC (opposite sides of parallelogram)

As DF∥ BC, DE∥ BC and DF = BC

But DE = EF
So, DF = 2(DE)
2(DE) = BC
DE = 1/2(BC)

Hence, proved that the line joining the mid-points of two sides of the triangle is parallel to the third side and is half of it.

Midpoint Formula

The midpoint of any line segment is defined as the coordinate point that divides the line segment into two equal parts.

Suppose P(x₁, y₁) and Q(x₂, y₂) are the coordinates of the endpoints of any line segment, then the midpoint formula is given as:

Midpoint = [(x₁ + x₂)/2, (y₁ + y₂)/2]

Converesre of Midpoint Theorem Proof

The line drawn through the mid-point of one side of a triangle parallel to the base of a triangle bisects the third side of the triangle.

• Given: In △PQR, S is the midpoint of PQ, and ST ∥ QR 
• To Prove: T is the midpoint of PR.
• Construction: Draw a line through R parallel to PQ and extend ST to U.

Proof:

• ST∥ QR   (given)
• So, SU∥ QR
• PQ∥ RU   (construction)

Therefore, Quadilateral SURQ is a parallelogram.

• SQ = RU   (Opposite sides of parallelogram)
• But SQ = PS   (S is the mid-point of PQ)
• Therefore, RU = PS

In △PST and △RUT

• ∠1 =∠2   (vertically opposite angles)
• ∠3 =∠4   (alternate angles)
• PS = RU  (proved above)

△PST ≅ △RUT by AAS criteria

Therefore, PT = RT

T is the mid-point of PR.

People Also Read:

• Quadrilateral
• Pythagoras Theorem
• Rhombus
• How to Find the Midpoint of a Line Segment?

Solved Examples of Midpoint Theorem

Example 1: l, m, and n are three parallel lines. p and q are two transversals intersecting parallel lines at A, B, C, D, E, and F as shown in the figure. If AB: BC = 1:1, find the ratio of DE: E F.

• Given: AB: BC = 1:1
• To find: DE: EF
• Construction: Join AF such that it intersects line m at G.

In △ACF 
AB = BC (1:1 ratio)
BG∥ CF (as m∥n)

Therefore, by converse of mid-point theorem G is the midpoint of AF (AG = GF)

Now, in △AFD

AG = GF (proved above)
GE∥ AD (as l∥m)

Therefore, by converse of mid-point theorem E is the mid-point of DF (FE = DE)

So, DE:EF = 1:1 (as they are equal)

Example 2: In the figure given below L, M and N are mid-points of side PQ, QR, and PR respectively of triangle PQR.

If PQ = 8cm, QR = 9cm and PR = 6cm. Find the perimeter of the triangle formed by joining L, M, and N.

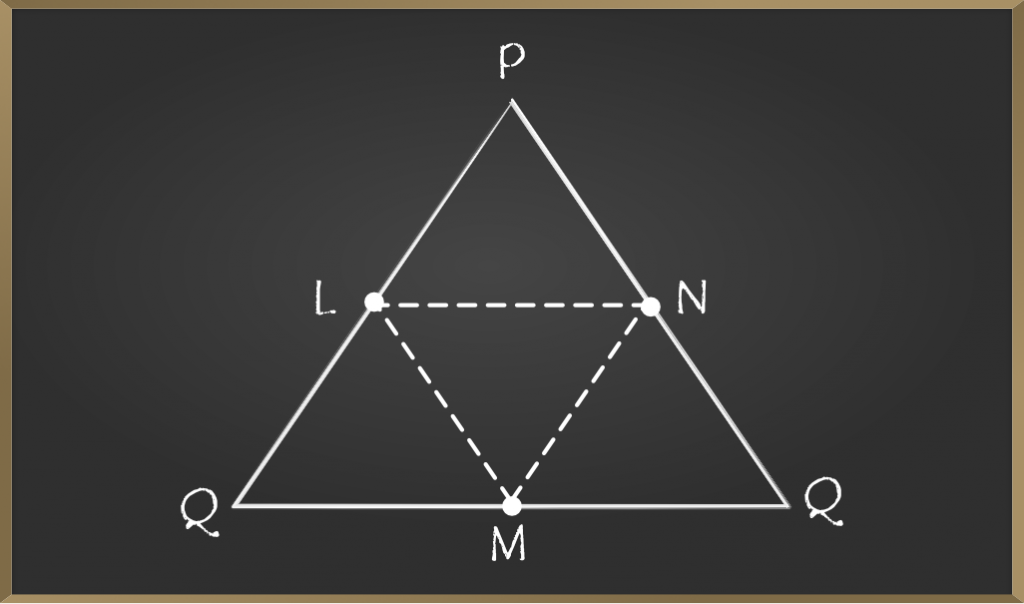
Solution:

As L and N are mid-points

By mid-point theorem 
LN ∥ QR and LN = 1/2 × (QR)
LN = 1/2 × 9 = 4.5cm

Similarly, LM = 1/2 × (PR) = 1/2×(6) = 3cm
Similarly, MN = 1/2 × (PQ) = 1/2 × (8) = 4cm

Therefore,
Perimeter of △LMN = LM + MN + LN
Perimeter of △LMN = 3 + 4 + 4.5 = 11.5 cm
Perimeter is 11.5cm

Practice Questions on Midpoint Theorem

Question 1: In triangle ABC, the midpoints of sides AB and AC are M and N, respectively. If MN is drawn parallel to side BC, and BC = 10 cm, what is the length of MN?

Question 2: Given, triangle PQR with midpoints S and T on sides PQ and PR, respectively. Prove that segment ST is parallel to side QR and that its length is half of QR.

Question 3: In triangle DEF, the vertices are at D(2, 3), E(6, 7), and F(4, 5). Find the coordinates of the midpoints G and H of sides DE and DF, respectively, and determine the length of segment GH.

Question 4: In quadrilateral ABCD, let M and N be the midpoints of sides AB and CD, respectively. If MN is drawn, show that MN Midpoint parallel to sides AD and BC.

Question 5: In triangle XYZ, let X(1, 1), Y(5, 3), and Z(3, 7). Find the lengths of segments connecting the midpoints of XY, XZ, and YZ. Verify the Midpoint Theorem.

Suggested Quiz

10 Questions

In a triangle, if the midpoints of two sides are connected, what can be inferred about the segment formed?

• A

  It is equal to the third side.

• B

  It is parallel to the third side and half of its length.

• C

  It is perpendicular to the third side.

• D

  It is longer than the third side.

Explanation:

According to the mid point theorem if a line joins the mid point of two sides of a triangle then it is parallel to the third side of the triangle and half of its length.

In triangle PQR, and M, N are midpoints of sides PQ and PR. If MN = x and QR = x + 4 , find the value of x.

• A

  4

• B

  6

• C

  2

• D

  8

Explanation:

according to mid point theorem
QR = 2MN

x + 4 = 2x

4 = 2x - x
x =4

Which of the following statements correctly describes the converse of the Midpoint Theorem?

• A

  The line joining the midpoints of two sides bisects the third side.

• B

  A line drawn through the midpoint of one side parallel to another side bisects the third side.

• C

  The midpoints of all three sides of a triangle are collinear.

• D

  The lengths of the sides of a triangle are equal.

Explanation:

The Converse of the Midpoint Theorem states:

If a line segment passing through mid point of one side of a triangle and is parallel to another of its sides , then it bisects the third side.

In triangle XYZ, M and N are midpoints of XY and XZ, respectively. If MN = 6 cm, what is the length of YZ?

• A

  6 cm

• B

  9 cm

• C

  12 cm

• D

  15 cm

Explanation:

Given, MN = 6 cm

According to the midpoint theorem the line joining the midpoints of two side of a triangle is parallel to the third side and half of its length,

then YZ = 2MN
Yz = 2 × 6 = 12 cm

In triangle DEF, if the midpoints of sides DE and DF are G and H respectively, what is the relationship between the area of triangle DGH and triangle DEF?

• A

  Area of DEF is equal to 1/4 × area of DGF.

• B

  Area of DGH is equal to 1/2 × area of DEF.

• C

  Area of DEF is equal to 4 × area of DGH.

• D

  Area of DGH is equal to 2 × area of DEF.

Explanation:

Given, G and H are the midpoints of DE and DF
then, DG = 1/2 × DE and DH = 1/2 × DF

now,, According to the mid point theorem : GH = 1/2 × EF

Now, by using heron's formula :
Area of DEF = [Tex]\sqrt{s_1(s_1-DE) \times s_1(s_1-EF) \times s_1(s_1-DF)}[/Tex] ........................ Where s₁ = (DE + DF + EF)/2
Area of DGH= [Tex]\sqrt{s_2(s_2-DE) \times s_2(s_2-EF) \times s_2(s_2-DF)}[/Tex] ........................ Where s₂ = (DG + DH +GH)/2

As we know
DG = DE/2 and DH = DF/2 and GH = EF/2
s₂ = s₁ /2

by using the above values we can say that : Area of DGH = 1/4 × Area of DEF ⇒ 4 × Area of DGH = Area of DEF

If triangle PQR has midpoints S and T on sides PQ and PR, What will be the ratio of perimeter of triangle PQR and PST?

• A

  2 : 1

• B

  1 : 2

• C

  1 : 4

• D

  4 : 1

Explanation:

Given, S and T are mid points of PQ and PR
then PS = PQ/2 and PT = PR/2

Now, according to mid point theorem

ST = QR/2

Since all the side of triangle PST are half of the sides of PQR

We can say that perimeter of PST = perimeter of PQR/2

hence the ratio will be 2 : 1

In a triangle, if the segment joining the midpoints of two sides is found to be longer than half the length of the third side, what can be concluded?

• A

  The triangle is not valid.

• B

  The midpoints are incorrectly identified.

• C

  The triangle is isosceles.

• D

  The theorem is not applicable to all triangles.

Explanation:

According to mid point theorem a line joining the mid- points of the two sides of a triangle is always parallel to the third side an its length is half of the third side.

the above condition clearly violates the mid point theorem thus it cannot be true.

In a triangle ABCD, E and F are midpoints of AB and BC, respectively. Which of the following is true?

• A

  EF = AC

• B

  EF is parallel to AC

• C

  EF is perpendicular to AC

• D

  [Tex]EF = \frac{1}{2}AC[/Tex]

Explanation:

As EF joins the mid point of the two sides of a triangle

Then, according to midpoint theorem

EF || AC and EF = 11/2 × AC

Which of the following is a necessary condition for the Midpoint Theorem to hold true in a triangle?

• A

  The triangle must be equilateral.

• B

  The triangle must have at least one right angle.

• C

  The triangle must be isosceles.

• D

  None of the above.

Explanation:

The mid point theorem is applicable to all triangles without any necessary condition.

If a line segment is drawn through the midpoint P of a side AB of a parallelogram and is parallel to another side BC and meets the diagonal AC at Q. Then, what is the ratio of length of AQ and QC ?

• A

  2: 1

• B

  1 : 2

• C

  None of the Above.

• D

  1 : 1

Explanation:

the diagonal AC divides the parallelogram into 2 triangle ABC and DBC

now in triangle the line passes through the mid point of AB and is parallel to BC

thus, by mid point theorem it will bisect the third side AC

hence, the ratio of length of AQ and QC = 1 : 1

Quiz Completed Successfully

Your Score :   2/10

Accuracy :  0%

Login to View Explanation

1/10 1/10 < Previous Next >