Polynomials| Degree | Types | Properties and Examples
Last Updated :
15 Feb, 2025
Polynomials are mathematical expressions made up of variables (often represented by letters like x, y, etc.), constants (like numbers), and exponents (which are non-negative integers). These expressions are combined using addition, subtraction, and multiplication operations.
A polynomial can have one or several terms. Each term is a product of a constant and a variable raised to an exponent.
For Example:
• x2,
• x2 + 2x,
• 5x + y,
• 3x3 + 5x2 – 4x,
• √2(x) + y, etc.
In the image added below, we have shown a polynomial, with variables, constants, and a leading coefficient:
Identifying Polynomials
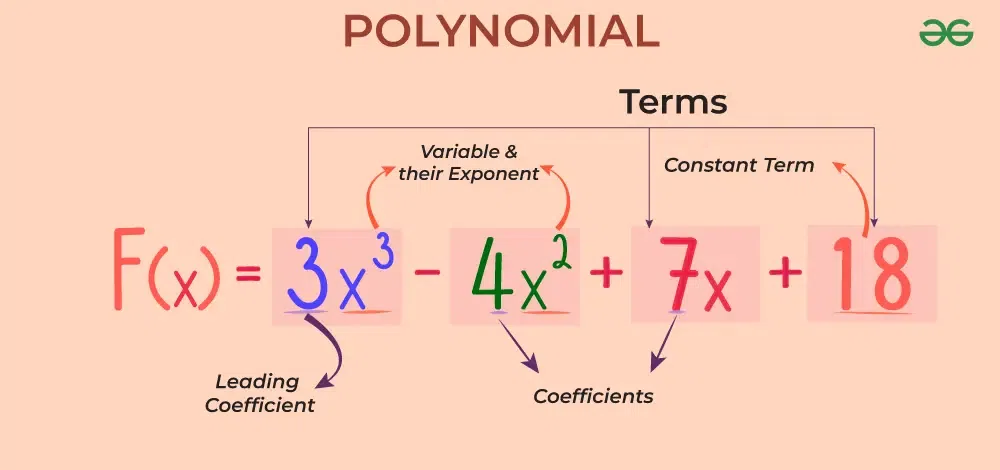
Degree of Polynomial
Degree of polynomial is determined by the highest exponent or power of the variable in the expression. It represents the highest degree term in the polynomial.
To find the degree of polynomial there are two cases:
Degree of Single Variable Polynomial
The degree of a single variable polynomial is determined by the highest exponent or power of that variable in the polynomial expression. It is represented by the highest degree term in the polynomial.
Example: 5x5 – 2x3 + 4x2 – x + 4
Solution:
The highest exponent is 5, which corresponds to the term 5x5. Therefore, the degree of this polynomial is 5.
Note: The degree of any polynomial which contains constant terms will be zero.
Degree of a Multivariable Polynomial
The degree of a multivariable polynomial is determined by the sum of the exponents of the variables in each term, considering the highest sum among all the terms.
Example: 5x2y3 – 2xy4 + 3x3+ 10
Solution:
In this expression, we have terms with variables x and y raised to different powers. To find the degree, we calculate the sum of the exponents for each term:
- First term, 5x2y3, has a sum of exponents equal to 2 + 3 = 5.
- Second term, -2xy4, has a sum of exponents equal to 1 + 4 = 5.
- Third term, 3x3, has a sum of exponents equal to 3.
Among all the terms the highest sum of exponents is 5. Therefore, the degree of this polynomial is 5.
|
Polynomial
|
Degree
|
Example
|
| Zero Polynomial |
Not Defined |
2 |
| Constant |
0 |
9 |
| Linear Polynomial |
1 |
2x + 1 |
| Quadratic Polynomial |
2 |
x2 + 3x + 2 |
| Cubic Polynomial |
3 |
5x3 + 7x2 + 3x + 9 |
| Biquadratic Polynomial |
4 |
8x4 + 9x3 + 1x2 + 2x + 5 |
Types of Polynomials
Polynomials can be categorized into several types based on the number of terms they contain or their degree.
Based on the Number of Terms:
- Monomial:
- A polynomial with just one term. For example, 7x3 or −4.
- Binomial:
- A polynomial with two terms. For example, x2 − 5x2.
- Trinomial:
- A polynomial with three terms. For example, 2x2 − 3x + 4.
- Multinomial:
- A polynomial with more than three terms. For example, x4 − 2x3 + 3x2 − x + 1.
Based on Degree:
- Constant Polynomial:
- A polynomial of degree 0. It has no variable terms, just a constant. For example, 5 or −3.
- Linear Polynomial:
- A polynomial of degree 1. It forms a straight line when graphed. For example, 3x + 2.
- Quadratic Polynomial:
- A polynomial of degree 2. It forms a parabolic shape when graphed. For example, x2 − 4x + 4.
- Cubic Polynomial:
- A polynomial of degree 3. It can have points of inflection and typically has the shape of an S-curve when graphed. For example, x3 − 6x2 + 11x − 6.
Read More: Types of Polynomials (Based on Terms and Degrees)
Standard Form of a Polynomial
P(x) = anxn + an−1 xn−1 + ⋯ + a1 x + a0
- an, an−1, …, a1, a0 are coefficients (which can be real or complex numbers).
- x is the variable.
- n is a non-negative integer representing the degree of polynomial.
- an is the leading coefficient and a0 is the constant term.
Each term consists of a variable raised to a non-negative whole number power, multiplied by a number.
Example: Express the variable in Standard form: x2 – 3x3 + 4x
Given Polynomial: x2 – 3x3 + 4x
In standard form polynomial is arranged in decreasing order of their degree = -3x3 + x2 + 4x
Terms in a Polynomial
In a polynomial various terms are separated using the plus (+) and the minus (-) sign. Depending on the number of terms in a polynomial a polynomial can be monomial, binomial, etc.
In a polynomial, we classify various terms into like terms and unlike terms.
- Like terms are the terms that have the same variable and with same exponent.
- Unlike terms are terms that have different variables or different powers(even with the same variable).
Read more about Like and Unlike Terms.
For example, Identify like terms and unlike terms in the polynomial, 4x3 + 2x2 -3xy + x3 – xy
Given Polynomial : 4x3 + 2x2 -3xy + x3 – xy
Like Terms: (4x3, x3) and (-3xy, -xy)
Unlike Terms: (4x3, x2), (x3, x2), (-3xy, x2), (-xy, x2), etc
Properties of Polynomials (Theorems of Polynomials)
Various properties of the polynomials are:
- For two polynomials P(x) and Q(x) :
Degree (P ± Q) ≤ max(deg P, deg Q)
Deg(P⋅Q) = deg P + deg Q
- For two given polynomials P(x) and Q(x) we always have unique polynomials Q (Quotient Polynomial) and R (Residue Polynomial) such that, P = R.Q + R
- If a polynomial P(x) is divisible by polynomial x – a, then P(a) = 0 is always true. This is also called Bezout’s Theorem or Factor Theorem.
- If a polynomial Q divides the polynomial P then zeros of polynomial Q are the zeros of polynomial P.
- For a polynomial of n degree, we have n roots that may be real or complex. The remainder of a polynomial f(x) when divided by (x – a) is f(a).
Solving Polynomials
Solving polynomials or solving polynomial equations means finding the roots or zeros of polynomials which are the values of the variable that make the equation true for a specific polynomial equation. There are various methods to find the root of the polynomial equations which often involve factorization of polynomials.
Zeroes of Polynomials: Zeros of a polynomial, also known as roots or solutions, are the values of the variable that make the polynomial equal to zero. In other words, they are the values of x for which the polynomial evaluates to zero.
If x is a zero of a given polynomial P(x) then p(x) = 0
Solving polynomial equations is a foundational skill in algebra and it is used in fields ranging from engineering to economics, where relationships defined by polynomials need to be analyzed and used.
Example: Solve x2 − 5x + 6 = 0
Solution:
Step 1: Set the Equation to Zero : Ensure your polynomial equation is in the standard form, where one side is zero. x2 − 5x + 6 = 0
Step 2: Factor the Polynomial : Factorize the polynomial into simpler binomial factors, if possible.
x2 − 5x + 6 = (x−2)(x−3).
Step 3: Apply the Zero Product Property : According to the zero product property, if a product equals zero, then at least one of the factors must be zero.
(x – 2) = 0 and (x – 3) = 0
Step 4: Solve for the Variable : Solve each equation from the previous step:
- From (x – 2) = 0, x = 2.
- From (x − 3) = 0, x = 3.
Step 5: Check Your Solutions : Substitute your solutions back into the original equation to verify:
- Put x=2 in x2 − 5x + 6 = 0 ⇒ (2)2 − 5(2) + 6 = 4 − 10 + 6 = 0
- Put x = 3 in x2 − 5x + 6 = 0⇒(3)2 − 5(3) + 6 = 9 − 15 + 6 = 0.
Articles related to Polynomials:
Question 1: Find the value of x in the polynomial equation 2x2 – 5x + 3 = 0.
Solution:
We can solve this quadratic equation using the quadratic formula:
x = (-b ± √(b2 – 4ac)) / 2a
where a = 2, b = -5, and c = 3.
Substituting the values:
x = (5 ± √(25 – 423)) / 2*2
x = (5 ± √(25 – 24)) / 4
x = (5 ± √1) / 4
So, the solutions are:
x = (5 + 1) / 4 = 6 / 4 = 3/2 and x = (5 – 1) / 4 = 4 / 4 = 1.
Question 2: Factorize the polynomial x2 – 4x + 4.
Solution:
We observe that the given polynomial is a perfect square trinomial.
It can be written as (x – 2)2.
So, the factored form is (x – 2)(x – 2) or (x – 2)2.
Question 3: Given the polynomial 3x4 – 7x3 + 2x2 – 5x + 1, find its degree and leading coefficient.
Solution:
The degree of a polynomial is the highest power of the variable present. In this case, the degree is 4. The leading coefficient is the coefficient of the term with the highest power of the variable. Here, the leading coefficient is 3.
Question 4: Simplify the expression (2x2 – 3x + 1)(x2 + 4x – 2).
Solution:
We use the distributive property to expand the expression:
(2x2 – 3x + 1)(x2 + 4x – 2) = 2x2(x2 + 4x − 2) − 3x(x2 + 4x − 2) + 1(x2 + 4x − 2)
= 2x4 + 8x3 − 4x2 − 3x3 − 12x2 + 6x + x2 + 4x − 2
= 2x4 + 5x3 – 15x2 + 10x – 2
Also Read:
Polynomial- FAQs
What is a Polynomial?
A polynomial is an expression that involves variables (usually represented by letters) raised to powers and combined using addition, subtraction, and multiplication. The variables can have coefficients (numbers multiplying the variables) attached to them.
What are Examples of Polynomials?
Some examples of polynomials are:
- 3x2 + 2x – 1,
- 4y3 – 5y + 2,
- 7a4 – 2b2, etc.
What is Zero of Polynomial?
Zeros of a polynomial is a the value of the polynomial substituting it in the polynomial results in Zero. Suppose we have a polynomial P(x) then zero of the polynomial is ‘a’ if P(a) is zero.
What is the the Coefficient of a Polynomial?
In a variable there are various terms and the coefficient of each term is called the coefficient of a polynomial. For example, in a polynomial x2 + 2x + 3
- Coefficient of x2 is 1
- Coefficient of 2x is 2
What is the Leading Coefficient of a Polynomial?
The coefficient of the highest degree term in the polynomial is called the leading coefficient of a polynomial.
What are Monomials, Binomials and Trinomials?
- Monomials are the polynomial with only one term. Example: 3x2
- Binomials are the polynomial with two terms. Example: 3x2 + 2x
- Trinomials are the polynomial with three terms. Example: 3x2 + 2x + 1
What is Constant in a Polynomial?
The constant term in the polynomial is the term with no variables. Suppose in the example, 3x2 + 2x + 1. The constant term is 1.
What are Polynomial Equations?
Equations which contains polynomials are called the polynomial equations various examples of the polynomial equations are,
- 3x3 + 8x – 5 = 0
- x + y + z = 0
- 3x + y – 5 = 0, etc.
The number of polynomials with zeros as ‒2 and 5 is?
There is 1 polynomial with zeros as -2 and 5, which is x2−3x−10.
Similar Reads
Algebra in Math - Definition, Branches, Basics and Examples
Algebra is the branch of mathematics with the following properties. Deals with symbols (or variables) and rules for manipulating these symbols. Elementary (Taught in Schools) Algebra mainly deals with variables and operations like sum, power, subtraction, etc. For example, x + 10 = 100, x2 - 2x + 1
3 min read
Algebraic Expression
Algebra Practice Questions Easy Level
Algebra questions basically involve modeling word problems into equations and then solving them. Some of the very basic formulae that come in handy while solving algebra questions are : (a + b) 2 = a 2 + b 2 + 2 a b(a - b) 2 = a 2 + b 2 - 2 a b(a + b) 2 - (a - b) 2 = 4 a b(a + b) 2 + (a - b) 2 = 2 (
3 min read
Algebraic Identities
Algebraic Identities are fundamental equations in algebra where the left-hand side of the equation is always equal to the right-hand side, regardless of the values of the variables involved. These identities play a crucial role in simplifying algebraic computations and are essential for solving vari
14 min read
Factorization of Polynomial
Factorization in mathematics refers to the process of expressing a number or an algebraic expression as a product of simpler factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, and we can express 12 as 12 = 1 Ã 12, 2 Ã 6, or 4 Ã 3. Similarly, factorization of polynomials involves expr
10 min read
Division of Algebraic Expressions
Division of algebraic expressions is a key operation in algebra. It is essential for simplifying expressions and solving equations. It is used to perform polynomial long division or synthetic division. Division of algebraic expressions is performed as as division on two whole numbers or fractions. I
6 min read
Polynomials
Polynomials| Degree | Types | Properties and Examples
Polynomials are mathematical expressions made up of variables (often represented by letters like x, y, etc.), constants (like numbers), and exponents (which are non-negative integers). These expressions are combined using addition, subtraction, and multiplication operations. A polynomial can have on
10 min read
Types of Polynomials (Based on Terms and Degrees)
Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n
9 min read
Zeros of Polynomial
Zeros of a Polynomial are those real, imaginary, or complex values when put in the polynomial instead of a variable, the result becomes zero (as the name suggests zero as well). Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing situation
14 min read
Geometrical meaning of the Zeroes of a Polynomial
An algebraic identity is an equality that holds for any value of its variables. They are generally used in the factorization of polynomials or simplification of algebraic calculations. A polynomial is just a bunch of algebraic terms added together, for example, p(x) = 4x + 1 is a degree-1 polynomial
8 min read
Multiplying Polynomials Worksheet
A polynomial is an algebraic expression consisting of variables and coefficients. We can perform various operations on polynomials, including addition, subtraction, multiplication, and division. This worksheet focuses on multiplying polynomials using different methods. Read More: Multiplying Polynom
4 min read
Dividing Polynomials | Long Division | Synthetic Division | Factorization Methods
Dividing Polynomials in maths is an arithmetic operation in which one polynomial is divided by another polynomial, where the divisor polynomial must have a degree less than or equal to the Dividend Polynomial otherwise division of polynomial can't take place. The most general form of a polynomial is
14 min read
Division Algorithm for Polynomials
Polynomials are those algebraic expressions that contain variables, coefficients, and constants. For Instance, in the polynomial 8x2 + 3z - 7, in this polynomial, 8,3 are the coefficients, x and z are the variables, and 7 is the constant. Just as simple Mathematical operations are applied on numbers
5 min read
Division Algorithm Problems and Solutions
Polynomials are made up of algebraic expressions with different degrees. Degree-one polynomials are called linear polynomials, degree-two are called quadratic and degree-three are called cubic polynomials. Zeros of these polynomials are the points where these polynomials become zero. Sometimes it ha
6 min read
Remainder Theorem
The Remainder Theorem is a simple yet powerful tool in algebra that helps you quickly find the remainder when dividing a polynomial by a linear polynomial, such as (x - a). Instead of performing long or synthetic division, you can use this theorem to substitute the polynomial and get the remainder d
9 min read
Factor Theorem
Factor theorem is used for finding the roots of the given polynomial. This theorem is very helpful in finding the factors of the polynomial equation without actually solving them. According to the factor theorem, for any polynomial f(x) of degree n ⥠1 a linear polynomial (x - a) is the factor of th
11 min read
Algebraic Identities of Polynomials
Algebraic identities are equations that hold true for all values of the variables involved. In the context of polynomials, these identities are particularly useful for simplifying expressions and solving equations. What are Algebraic Identities?Algebraic Identities are defined for the algebraic expr
10 min read
Factoring Polynomials
Factoring Polynomials: A basic algebraic concept called factoring polynomials involves breaking down a polynomial equation into simpler parts. Factoring can be used to solve equations, simplify complicated expressions, and locate the roots or zeros of polynomial functions. In several fields of math
9 min read
Relationship between Zeroes and Coefficients of a Polynomial
Polynomials are algebraic expressions with constants and variables that can be linear i.e. the highest power o the variable is one, quadratic and others. The zeros of the polynomials are the values of the variable (say x) that on substituting in the polynomial give the answer as zero. While the coef
9 min read
Linear Equations
Linear Equations in One Variable
Linear equation in one variable is the equation that is used for representing the conditions that are dependent on one variable. It is a linear equation i.e. the equation in which the degree of the equation is one, and it only has one variable. A linear equation in one variable is a mathematical sta
7 min read
Solving Linear Equations with Variable on both Sides
Equations consist of two main components: variables and numbers. Understanding the relationship between these components and how to manipulate them is essential for solving equations. Variable: A variable is a symbol (often a letter like x, y, or z) that represents an unknown or changing quantity.Nu
6 min read
Graphical Methods of Solving Pair of Linear Equations in Two Variables
A system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr
8 min read
Reducing Equations to Simpler Form | Class 8 Maths
Reducing equations is a method used to simplify complex equations into a more manageable form. This technique is particularly useful when dealing with non-linear equations, which cannot always be solved directly. By applying specific mathematical operations, such as cross-multiplication, these equat
7 min read
Linear Equation in Two Variables
Linear Equation in Two Variables: A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variables comes into the picture, it means that the entire equation has 2 variables presen
9 min read
Graph of Linear Equations in Two Variables
Linear equations are the first-order equations, i.e. the equations of degree 1. The equations which are used to define any straight line are linear, they are represented as, x + k = 0; These equations have a unique solution and can be represented on number lines very easily. Let's look at linear e
5 min read
Equations of Lines Parallel to the x-axis and y-axis
Linear Equations allow us to explain a lot of physical phenomena happening around us. For example, A train running between two stations at a constant speed, the speed of a falling object. Even the straight lines we draw on paper can be represented in form of linear equations mathematically. A linear
6 min read
Pair of Linear Equations in Two Variables
Linear Equation in two variables are equations with only two variables and the exponent of the variable is 1. This system of equations can have a unique solution, no solution, or an infinite solution according to the given initial condition. Linear equations are used to describe a relationship betwe
11 min read
Number of Solutions to a System of Equations Algebraically
A statement that two mathematical expressions of one or more variables are identical is called an equation. Linear equations are those in which the powers of all the variables concerned are equal. A linear equation's degree is always one. A solution of the simultaneous pair of linear equations is a
7 min read
Solve the Linear Equation using Substitution Method
A linear equation is an equation where the highest power of the variable is always 1. Its graph is always a straight line. A linear equation in one variable has only one unknown with a degree of 1, such as: 3x + 4 = 02y = 8m + n = 54a â 3b + c = 7x/2 = 8There are mainly two methods for solving simul
11 min read
Cross Multiplication Method
Cross multiplication method is one of the basic methods in mathematics that is used to solve the linear equations in two variables. It is one of the easiest to solve a pair of linear equations in two variables. Suppose we have a pair of linear equations in two variables, i.e. a1x + b1y = -c1 and a2
9 min read
Equations Reducible to Linear Form
Equations Reducible to Linear Form" refers to equations that can be transformed or rewritten into a linear equation. These equations typically involve variables raised to powers other than 1, such as squared terms, cubed terms, or higher. By applying suitable substitutions or transformations, these
9 min read
Quadratic Equations
Quadratic Equations
A Quadratic equation is a second-degree polynomial equation that can be represented as ax2 + bx + c = 0. In this equation, x is an unknown variable, a, b, and c are constants, and a is not equal to 0. The solutions of a quadratic equation are known as its roots. These roots can be found using method
11 min read
Solving Quadratic Equations
A quadratic equation, typically in the form ax² + bx + c = 0, can be solved using different methods including factoring, completing the square, quadratic formula, and the graph method. While Solving Quadratic Equations we try to find a solution that represent the points where this the condition Q(x)
8 min read
Roots of Quadratic Equation
Roots of Quadratic Equations are the values of the variable for which the quadratic equation gets satisfied. The roots of a quadratic equation are also called zeros of a quadratic equation. A quadratic equation is an equation in which the maximum power of a variable is 2. Hence, there can be a maxim
13 min read
Sequence and Series
Arithmetic Progression in Maths
Arithmetic Progression (AP) or Arithmetic Sequence is simply a sequence of numbers such that the difference between any two consecutive terms is constant. Some Real World Examples of AP Natural Numbers: 1, 2, 3, 4, 5, . . . with a common difference 1Even Numbers: 2, 4, 6, 8, 10, . . . with a common
3 min read
Arithmetic Series
An arithmetic series is the sum of the terms of an arithmetic sequence, where an arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. Or we can say that an arithmetic progression can be defined as a sequence of numbers in which for every pair of
5 min read
Arithmetic Sequence
An arithmetic sequence or progression is defined as a sequence of numbers in which the difference between one term and the next term remains constant. For example: the given below sequence has a common difference of 1. 1 2 3 4 5 . . . n â â â â â . . . 1st 2nd 3rd 4th 5th . . . nth Terms The Arithme
8 min read
Program to Check Geometric Progression
A sequence of numbers is called a Geometric progression if the ratio of any two consecutive terms is always the same. In simple terms, A geometric series is a list of numbers where each number, or term, is found by multiplying the previous term by a common ratio r. The general form of Geometric Prog
6 min read
Geometric Series
In a Geometric Series, every next term is the multiplication of its Previous term by a certain constant, and depending upon the value of the constant, the Series may increase or decrease. Geometric Sequence is given as: a, ar, ar2, ar3, ar4,..... {Infinite Sequence}a, ar, ar2, ar3, ar4, ....... arn
3 min read
Set Theory
Representation of a Set
Imagine a very haphazard world where no categories are divided to memorize and classify things separately, a world like this will be full of chaos and mess, this is why humans prefer to categorize things and classify them to neatly understand and remember them. The same case happens in mathematics,
8 min read
Types Of Sets
A well-defined collection of Objects or items or data is known as a set. The objects or data are known as the element. For Example, the boys in a classroom can be put in one set, all integers from 1 to 100 can become one set, and all prime numbers can be called an Infinite set. The symbol used for s
9 min read
Universal Sets
Universal Set is a set that has all the elements associated with a given set, without any repetition. Suppose we have two sets P = {1, 3, 5} and Q = {2, 4, 6} then the universal set of P and Q is U = {1, 2, 3, 4, 5, 6}. We generally use U to denote universal sets. Universal Set is a type of set that
6 min read
Venn Diagram
Venn Diagrams are used for the visual representation of relationships as they provide a clear, visual method for showing how different sets intersect, overlap, or remain distinct. They are essential tools in mathematics and logic for illustrating the relationships between sets. By employing intersec
15 min read
Operations on Sets
Sets are fundamental in mathematics and are collections of distinct objects, considered as a whole. In this article, we will explore the basic operations you can perform on sets, such as union, intersection, difference, and complement. These operations help us understand how sets interact with each
15+ min read
Union of Sets
Union of two sets means finding a set containing all the values in both sets. It is denoted using the symbol 'âª' and is read as the union. Example 1:If A = {1, 3. 5. 7} and B = {1, 2, 3} then AâªB is read as A union B and its value is,AâªB = {1, 2, 3, 5, 7} Example 2:If A = {1, 3. 5.7} and B = {2, 4}
13 min read
Cartesian Product of Sets
'Product' mathematically signifies the result obtained when two or more values are multiplied together. For example, 45 is the product of 9 and 5. One must be familiar with the basic operations on sets like Union and Intersection, which are performed on 2 or more sets. Cartesian Product is also one
7 min read
Relations and Functions
Relation and Function
In mathematics, we often deal with sets of numbers or objects and the ways they are connected to each other. Two important concepts that help us describe these connections are relations and functions. A relation is simply a connection between two sets of objects. Think of it as a rule that pairs ele
3 min read
Intoduction to Functions | Representation | Types | Examples
A function is a special relation or method connecting each member of set A to a unique member of set B via a defined relation. Set A is called the domain and set B is called the co-domain of the function. A function in mathematics from set A to set B is defined as, f = {(a,b)| â a â A, b â B} A func
14 min read
Types of Functions
Functions are defined as the relations which give a particular output for a particular input value. A function has a domain and codomain (range). f(x) usually denotes a function where x is the input of the function. In general, a function is written as y = f(x). Table of Content What is a Function?T
14 min read
Composite functions - Relations and functions
Let f : A->B and g : B->C be two functions. Then the composition of f and g, denoted by g o f, is defined as the function g o f : A->C given by g o f (x) = g{f(x)}, â x â A. Clearly, dom(g o f) = dom(f). Also, g o f is defined only when range(f) is a subset of dom(g). Evaluating composite f
5 min read
Invertible Functions
As the name suggests Invertible means "inverse", and Invertible function means the inverse of the function. Invertible functions, in the most general sense, are functions that "reverse" each other. For example, if f takes a to b, then the inverse, f-1, must take b to a. Table of Content Invertible F
15+ min read
Composition of Functions
The composition of functions is a process where you combine two functions into a new function. Specifically, it involves applying one function to the result of another function. In simpler terms, the output of one function becomes the input for the other function. Mathematically, the composition of
12 min read
Inverse Functions | Definition, Condition for Inverse and Examples
Inverse Functions are an important concept in mathematics. An inverse function basically reverses the effect of the original function. If you apply a function to a number and then apply its inverse, you get back the original number. For example, if a function turns 2 into 5, the inverse function wil
8 min read
Verifying Inverse Functions by Composition
A function can be seen as a mathematical formula or a machine that throws output when an input is given. The output is usually some processed version of the input. Function's inverses can be seen as the operations which give us the input back on giving them the output. In other words, inverse functi
5 min read
Domain and Range of a Function
In mathematics, a function represents a relationship between a set of inputs and their corresponding outputs. Functions are fundamental in various fields, from algebra to calculus and beyond, as they help model relationships and solve real-world problems. A function represents a relationship between
15+ min read
Piecewise Function
Piecewise Function is a function that behaves differently for different types of input. As we know a function is a mathematical object which associates each input with exactly one output. For example: If a function takes on any input and gives the output as 3. It can be represented mathematically as
11 min read