What is Monomial?
A monomial is a single-term algebraic expression. It can be a constant, a variable, or a product of numbers and variables where the variables have non-negative integer exponents. Monomials are the simplest forms of polynomials and are essential in algebraic expressions and equations.
In general, a monomial can be written as:
Where:
- a is a constant (also called the coefficient),
- x1, x2, . . ., xn are variables,
- k1, k2, . . . , kn are non-negative integers (the exponents).

Key points:
- A monomial always contains a single term.
- Variables must have non-negative integer exponents.
- No addition, subtraction, or division of terms or variables.
Parts of Monomials
The various parts of the monomial are covered in the below table with examples.
Parts of Monomials | Definition | Values in expression 7xy2 |
|---|---|---|
Variables | The letters are present in a monomial. | Variable: x and y |
Coefficient | The number that is multiplied by the variables. | Coefficient: 7 |
Degree | The sum of the exponents of the variables in a monomial. | Degree: (x degree) 1 + (y degree) 2 = 3 |
Example of Monomial
"Mono" refers to one. When polynomials are classified on the basis of the number of terms, the polynomials with only a single term are called monomials. Some of the examples of monomials are:
Constant Monomials
- 5
- -3.14
- 1000
Monomials with a Single Variable
- 2x
- -0.5y
- 4x2
- 0.25y3
Monomials with Multiple Variable
- 6xy
- -2.5yz2
- 3x2y3
Degree of Monomial
The sum of the exponents of the variables in a monomial gives us the degree of monomial.
This can be well understood by the following example.
The exponents of all the variables are added to determine a monomial's degree. It is always an integer that is not zero. For instance, the monomial xyz3 has a degree of 5.
- Variable 'x' has an exponent of 1,
- Variable 'y' has an exponent of 1, and
- Variable 'z' has an exponent of 3.
The result of adding all these exponents is 1 + 1 + 3 = 5.
Example 1: Find the degree of monomial -3x3y3.
Solution:
Here the exponent of x is 3
Exponent of y is 3
So degree = 3 + 3 = 6
Example 2: Find the degree of the monomial 9xy3.
Solution:
Degree of a monomial is given by the sum of exponents of the variables in a monomial.
Exponent of x = 1, Exponent of y = 3
Degree = 1 + 3 = 4
Identifying a Monomial
Let's apply the properties of a monomial in order to identify a monomial in the below examples:
Expression | Is it a Monomial? | Reason |
|---|---|---|
4xy2 | Yes | Single term, no addition, subtraction, or division involved. |
5x+y | No | Has two terms separated by addition operation |
4x/y | No | DenominatorsThe variable has a variable |
6x | No | The variable. is present in an exponent form |
Let's consider an example for better understanding.
Example: Identify if the following are monomial or not.
- x + 2y
- 7x2y
Solution:
• For x + 2y, Contains two terms that is x and 2y so it is not a monomial.
• For 7x2y, Contains a single term so it is a monomial.
Monomial Binomial and Trinomial
A monomial expression has, only one term. For example, 3xy is a monomial. A binary expression is one which has two terms. For example, 3x+4y, 4xy+6z is a binomial. Similar to this, a trinomial is an expression with three terms. For instance, a trinomial is 4x2 + 2y + 6z or 5x + 7xy + 9z .
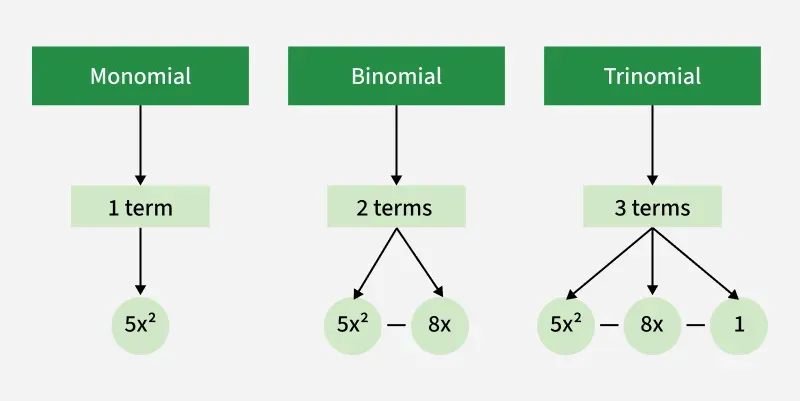
Lets look into the table below for more clarification between the three terms:
| Type | Definition | Example |
|---|---|---|
| Monomial | An algebraic expression consisting of a single term, which can be a constant, a variable, or a product of numbers and variables with non-negative integer exponents. | 5, x, 3x2, −7y3z |
| Binomial | An algebraic expression consisting of exactly two terms, which are separated by a plus (+) or minus (-) sign. | x + 5, 3x2 − 4x, y3 + 7z |
| Trinomial | An algebraic expression consisting of exactly three terms, which are separated by plus (+) or minus (-) signs. | x2 + 5x + 6, 3x2 − 4x + 7, y3 + y − 5 |
Note: Monomial is a type of polynomial. All monomial are polynomial but all polynomial aren't monomial.
Factors of Monomials
We usually factor coefficient and variables independently while factoring monomial. A monomial can be factored just as easily as a whole number.
Example: Factorize the monomial, 20y4.
In the given monomial, 20 is the coefficient and y4 is the variable.
- The prime factors of the coefficient, 20; are 2, 2, and 5.
- The variable y4 can be factored in as y × y × y × y.
Therefore, the complete factorization of the monomial is 20y4 = 2 × 2 × 5 × y × y × y × y.

Read More about Factoring Polynomial.
Operation on Monomials
Operations on monomials involve:
- Addition
- Subtraction
- Multiplication
- Division
Let's discuss these operations in detail as follows:
Addition of Monomials
To add two or more monomials that are like terms, add the coefficients; keep the variables and exponents on the variables the same.
Example: Add 10xy2 and -9xy2.
Solution:
In both monomials 10xy2 and -9xy2; xy2 is common.
Thus, 10xy2 + (-9xy2) = (10 + (-9))xy2 = xy2
Subtraction of Monomials
To subtract two or more monomials that are like terms, subtract the coefficients; keep the variables and exponents on the variables the same.
Example: Subtract 10xy2 and -9xy2
Solution:
Subtract the coefficient only
(10 - (-9))xy2 = 19xy2
Monomial Multiplication
To multiply a monomial by a monomial we get a monomial. The coefficients of the monomials are multiplied together and then the variables are multiplied.
Example: Find the product of two monomials 2x and 2y.
Solution:
Product of two monomial = 2x*2y = 4 xy
Monomial Division
To divide a monomial by a monomial, divide the coefficients and divide the variables with like bases by subtracting their exponents. To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
Example: Divide 4xy by 2x.
Solution:
Division of 4xy by 2x
= 4xy/2x = 2y
Read More,
Solved Problems on Monomials
Problem 1: Choose the monomials from the following expressions:
(a) x3
(b) 4 - x
Solution:
(a) x3 is a monomial as it has a single term.
(b) 4 -x isn't a monomial as it has two term.
Problem 2: Factorize the monomial expression: 8xy.
Solution:
In 8xy, the prime factors of coefficient 8 are 2 and 4. The variable part 'xy' can be split as x × y.
Therefore, the complete factorization of the monomial is 8xy = 2 × 4 × x × y.
Problem 3: Is 10y/x a monomial expression? Justify your answer.
Solution:
The expression has a single non-zero term, but the denominator of the expression is a variable. Therefore, the expression 10y/x is not a monomial.
Problem 4: Find the degree of monomial 48 xy3.
Solution:
Degree of monomial = sum of exponents of all variable
Thus, Degree of monomial = 1 + 3 = 4
Practice Problems on Monomials
Problem 1: Multiply the monomials: 4x3 and 2x2.
Problem 2: Simplify the expression: 3a4b2 · 5a2b3.
Problem 3: Divide the monomials: 8x5/4x2.
Problem 4: Add the monomials: 2x3 + 3x3.
Problem 5: Subtract the monomials: 7y4 - 2y4.
Problem 6: Find the product of the monomials: -2x4 · -3x2.

