倍立方問題
倍立方問題
倍立方是古希臘數學裏尺規作圖領域當中的著名問題,和三等分角、化圓為方問題被並列為古希臘尺規作圖三大難題。尺規作圖是古希臘人的數學研究課題之一,是對具體的直尺和圓規畫圖可能性的抽象化,研究是否能用規定的作圖法在有限步內達到給定的目標。倍立方問題的內容是:
「能否用尺規作圖的方法作出一立方體的稜長,使該立方體的體積等於一給定立方體的兩倍?」
倍立方問題的實質是能否通過尺規作圖從單位長度出發作出![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 的問題。
的問題。
三大難題提出後,在漫長的兩千餘年中,曾有眾多的嘗試,但沒有人能夠給出嚴格的答案。隨着十九世紀群論和域論的發展,法國數學家皮埃爾·汪策爾首先利用伽羅瓦理論證明,三等分角問題的答案是否定的。運用類似的方法,可以證明倍立方問題的答案同樣是否定的。具體來說,給定單位長度後,所有能夠經由尺規作圖達到的長度值被稱為規矩數,而如果能夠作出![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) ,那麼就能做出不屬於規矩數的長度,從而反證出通過尺規作圖作出給定立方體體積兩倍的立方體是不可能的。
,那麼就能做出不屬於規矩數的長度,從而反證出通過尺規作圖作出給定立方體體積兩倍的立方體是不可能的。
如果不將手段局限在尺規作圖法中,放寬限制或藉助更多的工具的話,作出給定立方體體積兩倍的立方體是可行的。
傳說中,這問題的來源,可追溯到公元前429年。一場瘟疫襲擊了希臘提洛島(Delos),造成四分之一的人口死亡。島民們去神廟請示阿波羅的旨意,神諭說:要想遏止瘟疫,得將阿波羅神殿中那正立方的祭壇加大一倍。人們便把每邊增長一倍,結果體積當然就變成了8倍,瘟疫依舊蔓延;接着人們又試著把體積改成原來的2倍,但形狀卻變為一個長方體……第羅斯島人在萬般無奈的情況下,只好鼓足勇氣到雅典去求救於當時著名的學者柏拉圖。
開始,柏拉圖和他的學生認為這個問題很容易。他們根據平時的經驗,覺得利用尺規作圖可以輕而易舉地作一個正方形,使它的面積等於已知正方形的2倍,那麼作一個正方體,使它的體積等於已知正方體體積的2倍,還會難嗎?
在敘述倍立方問題前,首先需要介紹尺規作圖。尺規作圖問題是從現實中具體的「直尺和圓規畫圖可能性」問題抽象出來的數學問題,將現實中的直尺和圓規抽象為數學上的設定,研究的是能不能在若干個具體限制之下,在有限的步驟內作出給定的圖形、結構或其他目標的問題。在尺規作圖中,直尺和圓規的定義是[1]:
- 直尺:一側為無窮長的直線,沒有刻度也無法標識刻度的工具。只可以讓筆摹下這個直線的全部或一部分。
- 圓規:由兩端點構成的工具。可以在保持兩個端點之間的距離不變的情況下,將兩個端點同時移動,或者只固定其中一個端點,讓另一個端點移動,作出圓弧或圓。兩個端點之間的距離只能取已經作出的兩點之間的距離,或者任意一個未知的距離。
定義了直尺和圓規的特性後,所有的作圖步驟都可以歸化為五種基本的步驟,稱為作圖公法[1]:
- 通過兩個已知點,作一直線。
- 已知圓心和半徑,作一個圓。
- 若兩已知直線相交,確定其交點。
- 若已知直線和一已知圓相交,確定其交點。
- 若兩已知圓相交,確定其交點。
尺規作圖研究的,就是是否能夠通過以上五種步驟的有限次重複,達到給定的作圖目標。尺規作圖問題常見的形式是:「給定某某條件,能否用尺規作出某某對象?」比如:「給定一個圓,能否用尺規作出這個圓的圓心?」,等等。[1]
倍立方問題的完整敘述是:
| “
|
任意給定一個線段l,是否能夠通過以上說明的五種基本步驟,於有限次內作出另一個長度的線段,使得以它為棱長的立方體的體積是以l為棱長的立方體的體積的2倍?
|
”
|
如果將給定線段的長度定為單位長度,則倍立方問題實質上就是要作出長度為單位長度的![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 倍的線段。[2]
倍的線段。[2]
與倍立方問題相比,倍平方問題要簡單得多。給定一個單位長度的線段,只需做一個以它為邊長的正方形,以正方形的對角線為邊長的正方形,面積就是2. 也即是說,尺規作圖可以作出長度為單位長度的 倍的線段。然而,
倍的線段。然而,![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 和
和 雖然形狀相近,卻有本質性的區別。數學家們直到十九世紀後,才從群論和域論的工具中了解了這個區別。
雖然形狀相近,卻有本質性的區別。數學家們直到十九世紀後,才從群論和域論的工具中了解了這個區別。
尺規作圖三大難題提出後,有許多基於平面幾何的論證和嘗試,但在十九世紀以前,一直沒有完整的解答。沒有人能夠給出倍立方問題的解法,但開始懷疑其可能性的人之中,也沒有人能夠證明這樣的解法一定不存在。直到十九世紀後,伽羅瓦和阿貝爾開創了以群論來討論有理系數多項式方程之解的方法,人們才認識到這三個問題的本質[1] 。
尺規可作性和規矩數
在研究各種尺規作圖問題的時候,數學家們留意到,能否用尺規作出特定的圖形或目標,本質是能否作出符合的長度。引進直角坐標系和解析幾何以後,又可以將長度解釋為坐標。比如說,作出一個圓,實際上是作出圓心的位置(坐標)和半徑的長度。作出特定的某個交點或某條直線,實際上是找出它們的坐標、斜率和截距。為此,數學家引入了尺規可作性這一概念。假設平面上有兩個已知的點O和A,以OA為單位長度,射線OA為x-軸正向可以為平面建立一個標準直角坐標系,平面中的點可以用橫坐標和縱坐標表示,整個平面可以等價於 。
。
設E是 的一個非空子集。如果某直線
的一個非空子集。如果某直線 經過E中不同的兩點,就說
經過E中不同的兩點,就說 是E-尺規可作的,簡稱E-可作。同樣地,如果某個圓
是E-尺規可作的,簡稱E-可作。同樣地,如果某個圓 的圓心和圓上的某個點是E中的元素,就說
的圓心和圓上的某個點是E中的元素,就說 是E-可作的。進一步地說,如果
是E-可作的。進一步地說,如果 里的某個點P是某兩個E-可作的直線或圓的交點(直線-直線、直線-圓以及圓-圓),就說點P是E-可作的。這樣的定義是基於五個基本步驟得來的,包括了尺規作圖中從已知條件得到新元素的五種基本方法。如果將所有E-尺規可作的點的集合記作s(E),那麼當E中包含超過兩個點的時候,E肯定是s(E)的真子集。從某個點集E0開始,經過一步能作出的點構成集合E1=s(E),經過兩步能作出的點就是E2=s(E1),……以此類推,經過n步能作出的點集就是En=s(En-1)。而所有從E能尺規作出的點集就是:
里的某個點P是某兩個E-可作的直線或圓的交點(直線-直線、直線-圓以及圓-圓),就說點P是E-可作的。這樣的定義是基於五個基本步驟得來的,包括了尺規作圖中從已知條件得到新元素的五種基本方法。如果將所有E-尺規可作的點的集合記作s(E),那麼當E中包含超過兩個點的時候,E肯定是s(E)的真子集。從某個點集E0開始,經過一步能作出的點構成集合E1=s(E),經過兩步能作出的點就是E2=s(E1),……以此類推,經過n步能作出的點集就是En=s(En-1)。而所有從E能尺規作出的點集就是:
 [3]:521
[3]:521
另一個與尺規可作性相關的概念是規矩數。設H是從集合E0={(0,0), (0,1)}開始,尺規可作點的集合: 那麼規矩數定義為H中的點的橫坐標和縱坐標表示的數。
那麼規矩數定義為H中的點的橫坐標和縱坐標表示的數。
- 定義:實數a和b是規矩數若且唯若(a, b)是H中的一個點。[3]:522
可以證明,有理數集 是所有規矩數構成的集合K的子集,而K又是實數集
是所有規矩數構成的集合K的子集,而K又是實數集 的子集。另外,為了在複數集
的子集。另外,為了在複數集 內討論問題,也會將平面
內討論問題,也會將平面 看作複平面
看作複平面 ,同時定義一個複數a+bi是(復)規矩數若且唯若點(a, b)是H中的一個點。所有復規矩數構成的集合L也包含
,同時定義一個複數a+bi是(復)規矩數若且唯若點(a, b)是H中的一個點。所有復規矩數構成的集合L也包含 作為子集,並且是複數集
作為子集,並且是複數集 的子集。從尺規可作性到解析幾何下的規矩數,尺規作圖問題從幾何問題轉成了代數的問題。[3]:522
的子集。從尺規可作性到解析幾何下的規矩數,尺規作圖問題從幾何問題轉成了代數的問題。[3]:522
域的擴張與最小多項式
以集合的觀念來說,L與 、
、 之間是子集與包含的關係。以抽象代數的觀點來說,可以證明L是有理數域
之間是子集與包含的關係。以抽象代數的觀點來說,可以證明L是有理數域 的擴域,是實數域
的擴域,是實數域 的子域。記作
的子域。記作 。域是抽象代數中的概念,是能夠進行「加減乘除」運算的集合。從單位長度出發,很容易得到任何有理數長度的線段,所以直線OA(也就是實數軸)上所有的有理數坐標的點都是尺規可作點[1]。如果平面上還有另一個尺規可作點(對應複數z),那麼也能做出任意pz+q的點,甚至於任何形如:
。域是抽象代數中的概念,是能夠進行「加減乘除」運算的集合。從單位長度出發,很容易得到任何有理數長度的線段,所以直線OA(也就是實數軸)上所有的有理數坐標的點都是尺規可作點[1]。如果平面上還有另一個尺規可作點(對應複數z),那麼也能做出任意pz+q的點,甚至於任何形如:

的點(其中P1和P2是兩個多項式)。有理數域 和所有因為z而多出來的尺規可作點仍舊構成一個域,稱為
和所有因為z而多出來的尺規可作點仍舊構成一個域,稱為 關於z的擴張,記作
關於z的擴張,記作 。然而,
。然而, 中的元素並沒有表面上那麼「多」。一般來說,如果有一個多項式P使得P(z)=0,那麼
中的元素並沒有表面上那麼「多」。一般來說,如果有一個多項式P使得P(z)=0,那麼 中的元素都可以寫成λ1+λ2z+...+λdzd-1的形式,其中d是P的階數。這樣的情況稱為域
中的元素都可以寫成λ1+λ2z+...+λdzd-1的形式,其中d是P的階數。這樣的情況稱為域 的有限擴張,因為
的有限擴張,因為 可以看成關於
可以看成關於 的有限維線性空間。為了確定這個線性空間的維數,需要為它找一個基底,也就是一個線性無關的最小生成集。為此,尋找使得m(z)=0的多項式中階數最小的,並稱m是z最小多項式。在最小多項式確定後,便可確定1, z, ... , zdm-1是
的有限維線性空間。為了確定這個線性空間的維數,需要為它找一個基底,也就是一個線性無關的最小生成集。為此,尋找使得m(z)=0的多項式中階數最小的,並稱m是z最小多項式。在最小多項式確定後,便可確定1, z, ... , zdm-1是 的一個基底,
的一個基底, 是一個dm維的
是一個dm維的 -線性空間(dm是m的階數)[4]:68。這時候也稱dm是域擴張
-線性空間(dm是m的階數)[4]:68。這時候也稱dm是域擴張 的階數,記作:
的階數,記作:
![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=\mathrm {d} _{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ced33e4acb0aa7576ffc60ea3ad8e34c02878a) [3]:512
[3]:512
規矩擴張的階數
對任何一個尺規可作點,都可以考察它對應的域擴張的階數。由於每個尺規可作點都是通過五種作圖公法的有限次累加得到的,而其中生成新點(也就是新坐標)的只有後三種。所以只需考察這三種步驟得到的新點對應的域擴張的階數。假設某個時刻,已知的所有尺規可作點構成的域是L,那麼生成新點時的直線和圓的係數都在L裏面。
- 直線的方程是:

- 圓的方程是:

無論是兩個(1)類方程,兩個(2)類方程,還是一個(1)類和一個(2)類方程聯立求解,得到的x和y值都會是形同

的數值。所以復規矩數z=x+yi滿足一個二次方程:

其中的p1+p2i、q1+q2i以及t都是L中的元素[3]:523[4]:78-79。這意味着,域擴張L⊆L(z)的階數最多是2(最小多項式的階數至多是2)[1]。這又說明,從L開始,經過一系列(n次)基本步驟得到的尺規可作點,代表了n次域擴張:

而每次域擴張的階數:[Lk : Lk-1]都不超過2。因此,如果從基本的有理數域出發的話,就能得到如下的定理:[3]:523-524[1]
任何復規矩數z對應的域擴張 的階數 的階數![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9605b4fbc7591aab8d58d5940bf3c64dedc35c) 都是2的某個冪次: 都是2的某個冪次:
![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=2^{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/763c96a7d518f88168e19011d3b7d818020ec18d)
|
其中
的s是某個小於
n的自然數(
n是已知所有有理數坐標點時,
作出z對應的點要經過的基本步驟數
目)。
倍立方不可能性的證明
[編輯]證明使用反證法。倍立方問題是指已知單位長度1,要作出![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 的長度。反設
的長度。反設![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 可以作出,說明它是一個規矩數。所以域擴張的階數
可以作出,說明它是一個規矩數。所以域擴張的階數![{\displaystyle [\mathbb {Q} ({\sqrt[{3}]{2}}):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aa48dee58391eb1afb75f3e9485472acf5ec837) 應該是2的冪次。然而,
應該是2的冪次。然而,![{\displaystyle z={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f70edbdce5fcc7defda48f303a81f3e5584e8d9) 的最小多項式是:
的最小多項式是:

這說明域擴張![{\displaystyle \mathbb {Q} \subseteq \mathbb {Q} ({\sqrt[{3}]{2}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edcc3da5b9d31c47e990f09d9d4a533cb9e43715) 的階數是3,不是2的冪次,這與先前的結論矛盾。所以,用尺規方法無法作出一個立方體,使得它的體積是已知立方體的兩倍。
的階數是3,不是2的冪次,這與先前的結論矛盾。所以,用尺規方法無法作出一個立方體,使得它的體積是已知立方體的兩倍。
如果放寬條件,比如使用有刻度的直尺(二刻尺)或摺紙等,則倍立方是有可能的:
 用有刻度的直尺來進行倍立方
用有刻度的直尺來進行倍立方
- 作一個邊長為 1 的等邊三角形 ABC。
- 把 AB 延長,作線 AD ,使得 BD = 1。
- 把 BC 延長,作線 BE。
- 把 D 和 C 相連並延長,作線 DF。
- 利用直尺上的刻度,作線 AGH,使得 GH = 1 ,其中 G 和 H 分別在 DF 和 BE 之上。
- AG 的長度就是
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) ,作圖完畢
,作圖完畢
由

得

又根據畢氏定理

現在設 ,則
,則 由孟氏定理
由孟氏定理

可得

兩邊平方後整理



此方程式有唯一正實根
![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)
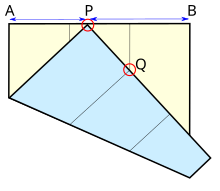 通過摺紙的方式求出2的立方根
通過摺紙的方式求出2的立方根
將一張正方形紙折三等份留下痕跡之後,點P折向正方形的邊AB,並且點P的位置要使得左三等分點Q折到與右三等分線重合。此時有![{\displaystyle {\frac {\overline {PB}}{\overline {AP}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d20116cf0782d238d56f6a178d9a108be43b8d) 。
。
將圖中左邊被折的點命名為C,以及AB邊上右三等分點命名為D。
設正方形連長為1以及AC長度為 ,則有CP長度為
,則有CP長度為 ,AP長度通過勾股定理為
,AP長度通過勾股定理為 ;另一方面PQ長度為
;另一方面PQ長度為 ,PD長度為
,PD長度為 。
。
根據相似三角形( ),可以得到方程:
),可以得到方程:

取其正根解得![{\displaystyle x={\frac {2}{3}}-{\frac {1}{3{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c8a1478f6088306793b377dfc26960ca7d3479) ,又由於PB長度為
,又由於PB長度為 ,於是代入
,於是代入![{\displaystyle x={\frac {2}{3}}-{\frac {1}{3{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c8a1478f6088306793b377dfc26960ca7d3479) 得
得![{\displaystyle {\frac {1-{\sqrt {1-2x}}}{\sqrt {1-2x}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b62c8fcc596900a53dae424d36e9c4961b21c1fa) ,證畢。
,證畢。




![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)













![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=\mathrm {d} _{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ced33e4acb0aa7576ffc60ea3ad8e34c02878a)





![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9605b4fbc7591aab8d58d5940bf3c64dedc35c)
![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=2^{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/763c96a7d518f88168e19011d3b7d818020ec18d)
![{\displaystyle [\mathbb {Q} ({\sqrt[{3}]{2}}):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aa48dee58391eb1afb75f3e9485472acf5ec837)
![{\displaystyle z={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f70edbdce5fcc7defda48f303a81f3e5584e8d9)

![{\displaystyle \mathbb {Q} \subseteq \mathbb {Q} ({\sqrt[{3}]{2}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edcc3da5b9d31c47e990f09d9d4a533cb9e43715)










![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)
![{\displaystyle {\frac {\overline {PB}}{\overline {AP}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d20116cf0782d238d56f6a178d9a108be43b8d)







![{\displaystyle x={\frac {2}{3}}-{\frac {1}{3{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c8a1478f6088306793b377dfc26960ca7d3479)

![{\displaystyle {\frac {1-{\sqrt {1-2x}}}{\sqrt {1-2x}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b62c8fcc596900a53dae424d36e9c4961b21c1fa)