Rabin-Karp Algorithm for Pattern Searching

In many data structures and algorithms (DSA) problems, one common task is to compare strings—whether it’s finding a word in a sentence, detecting duplicates, or checking for patterns inside a larger text.
Think of this like trying to find a short phrase inside a big paragraph—manually checking every character would be tiring. Computers do the same thing, and if we’re not careful, it can become very slow for long texts.
That’s where the Rabin-Karp algorithm comes in.
It was developed by Michael Rabin and Richard Karp in 1987 as a clever way to speed up pattern matching using hashing techniques. Instead of comparing characters one by one, it converts the strings into numbers (hashes) and compares those—just like how barcodes are used in stores instead of reading the full product name.
In short, Rabin-Karp is:
- A string matching algorithm
- Uses rolling hash to find all occurrences of a pattern in a text
- Optimized for cases where multiple patterns or repeated matching is required
This forms the foundation for many modern algorithms in plagiarism detection, substring search, and more.
Table of Content
Why is Rabin-Karp Needed?
Let’s say you want to find if the word "code" appears inside a big article.
The simplest way? Start from the first letter and check every group of 4 letters one by one. This is known as the naive approach, and it works fine—but it checks every character every time, which can be very slow if the text is long.
The naive method has a time complexity of O(n × m), where:
- n = length of the text
- m = length of the pattern
Now imagine trying to find multiple patterns (like checking 100 different words in a document). Doing this the naive way becomes painfully slow.
Rabin-Karp improves this by using rolling hash.
Instead of comparing actual characters every time, it converts both the pattern and parts of the text into numbers (hashes) and compares those numbers. This way, most of the time it can detect mismatches without looking at every character, making it much faster and scalable.
Key Idea of Rabin-Karp
The main idea behind Rabin-Karp is to convert strings into numeric hashes so we can compare numbers instead of characters. This makes the process much faster.
To do this efficiently, we use a rolling hash, which allows us to compute the hash of the next substring in constant time by updating the previous hash. So instead of rechecking every character, we just slide the window and adjust the hash.
We first compute the hash of the pattern, then compare it with the hashes of all substrings of the text. If the hashes match, we do a quick character-by-character check to confirm (to avoid errors due to hash collisions).
This way, most comparisons are done using numbers, making pattern matching fast and scalable, especially for large texts or multiple patterns.
How is Hash Value calculated in Rabin-Karp?
The hash value in Rabin-Karp is calculated using a rolling hash function, which allows efficient hash updates as the pattern slides over the text. Instead of recalculating the entire hash for each substring, the rolling hash lets us remove the contribution of the old character and add the new one in constant time.
A string is converted into a numeric hash using a polynomial rolling hash. For a string s of length n, the hash is computed as:
=> hash(s) = (s[0] * p(n-1) + s[1] * p(n-2) + ... + s[n-1] * p0 ) %mod
Where:
- s[i] is the numeric value of the i-th character ('a' = 1, 'b' = 2, ..., 'z' = 26)
- p is a small prime number (commonly 31 or 37)
- mod is a large prime number (like 1e9 + 7) to avoid overflow and reduce hash collisions
This approach allows us to compute hash values of substrings in constant time using precomputed powers and prefix hashes.
Hash Recurrence Relation
Let preHash[i] represent the hash of the prefix substring s[0...i].
Then the recurrence is: preHash[i] = preHash[i - 1] * base + s[i]
Where:
- p[0] = s[0]
- s[i] is the numeric value of the i-th character ('a' = 1, 'b' = 2, ..., 'z' = 26)
- base is a chosen prime number (commonly 31 or 37)
- All operations are done under modulo mod to avoid overflow
How to Calculate Hash from L to R ?
To get the hash of any substring s[L...R] efficiently, we use prefix hashing.
First, we precompute prefix hashes, where prefix[i] stores the hash of the substring s[0...i]. Alongside, we also precompute powers of the base (like base^1, base^2, etc.) to help in quick calculations.
Then, using modular arithmetic, we can calculate the hash of any range in constant time with the formula:
hash(L, R) = (prefix[R] - prefix[L-1] * power(R - L + 1) + mod) % mod
Here,
- prefix[R] is the hash from 0 to R
- prefix[L-1] * power(R - L + 1) removes the contribution of the first L characters
- + mod ensures the result stays positive before applying % mod
class RabinKarpHash {
private:
const int mod = 1e9 + 7;
const int base = 31;
vector<int> hash;
vector<int> power;
// modular addition
int add(int a, int b) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
int sub(int a, int b) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
int mul(int a, int b) {
return (int)((1LL * a * b) % mod);
}
// convert character to int
// ('a' = 1, ..., 'z' = 26)
int charToInt(char c) {
return c - 'a' + 1;
}
public:
// constructor: precomputes prefix hashes and powers
RabinKarpHash(string &s) {
int n = s.size();
hash.resize(n);
power.resize(n);
hash[0] = charToInt(s[0]);
power[0] = 1;
for (int i = 1; i < n; ++i) {
hash[i] = add(mul(hash[i - 1], base), charToInt(s[i]));
power[i] = mul(power[i - 1], base);
}
}
// get hash of substring s[l...r] in O(1)
int getSubHash(int l, int r) {
int h = hash[r];
if (l > 0) {
h = sub(h, mul(hash[l - 1], power[r - l + 1]));
}
return h;
}
};
class GfG {
private final int mod = (int)1e9 + 7;
private final int base = 31;
private int[] hash;
private int[] power;
// modular addition
private int add(int a, int b) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
private int sub(int a, int b) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
private int mul(int a, int b) {
return (int)((1L * a * b) % mod);
}
// convert character to int
// ('a' = 1, ..., 'z' = 26)
private int charToInt(char c) {
return c - 'a' + 1;
}
// constructor: precomputes prefix hashes and powers
public GfG(String s) {
int n = s.length();
hash = new int[n];
power = new int[n];
hash[0] = charToInt(s.charAt(0));
power[0] = 1;
for (int i = 1; i < n; i++) {
hash[i] = add(mul(hash[i - 1], base), charToInt(s.charAt(i)));
power[i] = mul(power[i - 1], base);
}
}
// get hash of substring s[l...r] in O(1)
public int getSubHash(int l, int r) {
int h = hash[r];
if (l > 0) {
h = sub(h, mul(hash[l - 1], power[r - l + 1]));
}
return h;
}
}
class RabinKarpHash:
def __init__(self, s):
self.mod = int(1e9) + 7
self.base = 31
n = len(s)
self.hash = [0] * n
self.power = [0] * n
# convert character to int
# ('a' = 1, ..., 'z' = 26)
def charToInt(c):
return ord(c) - ord('a') + 1
self.hash[0] = charToInt(s[0])
self.power[0] = 1
for i in range(1, n):
self.hash[i] = (self.hash[i - 1] * self.base \
+ charToInt(s[i])) % self.mod
self.power[i] = (self.power[i - 1] * \
self.base) % self.mod
# get hash of substring s[l...r] in O(1)
def getSubHash(self, l, r):
h = self.hash[r]
if l > 0:
h = (h - self.hash[l - 1] * \
self.power[r - l + 1]) % self.mod
if h < 0:
h += self.mod
return h
using System;
class GfG {
private readonly int mod = (int)1e9 + 7;
private readonly int baseVal = 31;
private int[] hash;
private int[] power;
// modular addition
private int add(int a, int b) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
private int sub(int a, int b) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
private int mul(int a, int b) {
return (int)(((long)a * b) % mod);
}
// convert character to int
// ('a' = 1, ..., 'z' = 26)
private int charToInt(char c) {
return c - 'a' + 1;
}
// constructor: precomputes prefix hashes and powers
public GfG(string s) {
int n = s.Length;
hash = new int[n];
power = new int[n];
hash[0] = charToInt(s[0]);
power[0] = 1;
for (int i = 1; i < n; i++) {
hash[i] = add(mul(hash[i - 1], baseVal),
charToInt(s[i]));
power[i] = mul(power[i - 1], baseVal);
}
}
// get hash of substring s[l...r] in O(1)
public int getSubHash(int l, int r) {
int h = hash[r];
if (l > 0) {
h = sub(h, mul(hash[l - 1], power[r - l + 1]));
}
return h;
}
}
class RabinKarpHash {
constructor(s) {
this.mod = 1e9 + 7;
this.base = 31;
this.hash = [];
this.power = [];
// convert character to int
// ('a' = 1, ..., 'z' = 26)
const charToInt = (c) => {
return c.charCodeAt(0) - 'a'.charCodeAt(0) + 1;
};
// modular addition
const add = (a, b) => {
a += b;
if (a >= this.mod) a -= this.mod;
return a;
};
// modular multiplication
const mul = (a, b) => {
return Math.floor((a * b) % this.mod);
};
const n = s.length;
this.hash[0] = charToInt(s[0]);
this.power[0] = 1;
for (let i = 1; i < n; i++) {
this.hash[i] = add(mul(this.hash[i - 1], this.base),
charToInt(s[i]));
this.power[i] = mul(this.power[i - 1], this.base);
}
// store inner functions for access in getSubHash
this._add = add;
this._sub = (a, b) => {
a -= b;
if (a < 0) a += this.mod;
return a;
};
this._mul = mul;
}
// get hash of substring s[l...r] in O(1)
getSubHash(l, r) {
let h = this.hash[r];
if (l > 0) {
h = this._sub(h, this._mul(this.hash[l - 1],
this.power[r - l + 1]));
}
return h;
}
}
Time Complexity: O(n), the prefix hashes and powers are precomputed in a single pass over the string, which takes linear time. Once built, any substring hash can be retrieved in O(1) time.
Auxiliary Space: O(n), two arrays of size n are used to store the prefix hashes and powers of the base, resulting in linear extra space usage.
Practical Example for Better Understanding
Given two strings text (the text) and pattern (the pattern), consisting of lowercase English alphabets, find all 0-based starting indices where pattern occurs as a substring in text.
Examples:
Input: text = "geeksforgeeks", pattern = "geeks"
Output: [0, 8]
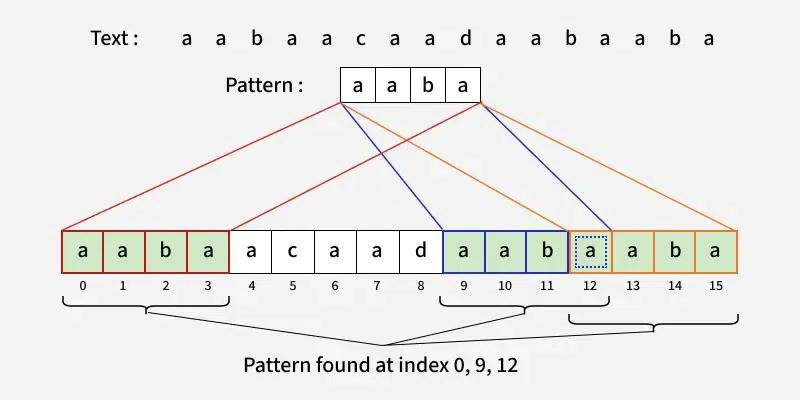
Explanation: The string "geeks" occurs at index 0 and 8 in text.Input: text = "aabaacaadaabaaba", pattern = "aaba"
Output: [0, 9, 12]
Explanation:
In the Naive String Matching algorithm, we check whether every substring of the text of the pattern's size is equal to the pattern or not one by one.
Like the Naive Algorithm, the Rabin-Karp algorithm also check every substring. But unlike the Naive algorithm, the Rabin Karp algorithm matches the hash value of the pattern with the hash value of the current substring of text, and if the hash values match then only it starts matching individual characters. So Rabin Karp algorithm needs to calculate hash values for the following strings.
- Pattern itself
- All the substrings of the text of length m which is the size of pattern.
#include <iostream>
#include <vector>
#include <string>
using namespace std;
class RabinKarpHash {
private:
const int mod = 1e9 + 7;
const int base = 31;
vector<int> hash;
vector<int> power;
// modular addition
int add(int a, int b) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
int sub(int a, int b) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
int mul(int a, int b) {
return (int)((1LL * a * b) % mod);
}
// convert character to int
// ('a' = 1, ..., 'z' = 26)
int charToInt(char c) {
return c - 'a' + 1;
}
public:
// constructor: precomputes prefix hashes and powers
RabinKarpHash(string &s) {
int n = s.size();
hash.resize(n);
power.resize(n);
hash[0] = charToInt(s[0]);
power[0] = 1;
for (int i = 1; i < n; ++i) {
hash[i] = add(mul(hash[i - 1], base), charToInt(s[i]));
power[i] = mul(power[i - 1], base);
}
}
// get hash of substring s[l...r] in O(1)
int getSubHash(int l, int r) {
int h = hash[r];
if (l > 0) {
h = sub(h, mul(hash[l - 1], power[r - l + 1]));
}
return h;
}
};
// Rabin-Karp search using hash class
vector<int> searchPattern(string &text, string &pattern) {
int n = text.size(), m = pattern.size();
RabinKarpHash textHash(text);
RabinKarpHash patHash(pattern);
int patternHash = patHash.getSubHash(0, m - 1);
vector<int> result;
for (int i = 0; i <= n - m; i++) {
int subHash = textHash.getSubHash(i, i + m - 1);
if (subHash == patternHash) {
result.push_back(i);
}
}
return result;
}
int main() {
string txt = "geeksforgeeks";
string pat = "geek";
vector<int> positions = searchPattern(txt, pat);
for (int idx : positions) {
cout << idx << " ";
}
cout << endl;
return 0;
}
import java.util.ArrayList;
class RabinKarpHash {
private final int mod = 1000000007;
private final int base = 31;
private int[] hash;
private int[] power;
// modular addition
private int add(int a, int b) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
private int sub(int a, int b) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
private int mul(int a, int b) {
return (int)((1L * a * b) % mod);
}
// convert character to int
// ('a' = 1, ..., 'z' = 26)
private int charToInt(char c) {
return c - 'a' + 1;
}
// constructor: precomputes prefix hashes and powers
public RabinKarpHash(String s) {
int n = s.length();
hash = new int[n];
power = new int[n];
hash[0] = charToInt(s.charAt(0));
power[0] = 1;
for (int i = 1; i < n; ++i) {
hash[i] = add(mul(hash[i - 1], base), charToInt(s.charAt(i)));
power[i] = mul(power[i - 1], base);
}
}
// get hash of substring s[l...r] in O(1)
public int getSubHash(int l, int r) {
int h = hash[r];
if (l > 0) {
h = sub(h, mul(hash[l - 1], power[r - l + 1]));
}
return h;
}
}
class GfG {
// Rabin-Karp search using hash class
public static ArrayList<Integer> searchPattern(String text, String pattern) {
int n = text.length(), m = pattern.length();
RabinKarpHash textHash = new RabinKarpHash(text);
RabinKarpHash patHash = new RabinKarpHash(pattern);
int patternHash = patHash.getSubHash(0, m - 1);
ArrayList<Integer> result = new ArrayList<>();
for (int i = 0; i <= n - m; i++) {
int subHash = textHash.getSubHash(i, i + m - 1);
if (subHash == patternHash) {
result.add(i);
}
}
return result;
}
public static void main(String[] args) {
String txt = "geeksforgeeks";
String pat = "geek";
ArrayList<Integer> positions = searchPattern(txt, pat);
for (int idx : positions) {
System.out.print(idx + " ");
}
System.out.println();
}
}
class RabinKarpHash:
def __init__(self, s):
self.mod = 10**9 + 7
self.base = 31
n = len(s)
self.hash = [0] * n
self.power = [0] * n
# convert character to int
# ('a' = 1, ..., 'z' = 26)
def charToInt(c):
return ord(c) - ord('a') + 1
self.hash[0] = charToInt(s[0])
self.power[0] = 1
for i in range(1, n):
self.hash[i] = (self.hash[i - 1] * self.base \
+ charToInt(s[i])) % self.mod
self.power[i] = (self.power[i - 1] * self.base)\
% self.mod
# get hash of substring s[l...r] in O(1)
def getSubHash(self, l, r):
h = self.hash[r]
if l > 0:
h = (h - self.hash[l - 1] * self.power[r - l + 1]) % self.mod
if h < 0:
h += self.mod
return h
# Rabin-Karp search using hash class
def searchPattern(text, pattern):
n, m = len(text), len(pattern)
textHash = RabinKarpHash(text)
patHash = RabinKarpHash(pattern)
patternHash = patHash.getSubHash(0, m - 1)
result = []
for i in range(n - m + 1):
subHash = textHash.getSubHash(i, i + m - 1)
if subHash == patternHash:
result.append(i)
return result
if __name__ == "__main__":
txt = "geeksforgeeks"
pat = "geek"
positions = searchPattern(txt, pat)
print(*positions)
using System;
using System.Collections.Generic;
class RabinKarpHash {
private readonly int mod = 1000000007;
private readonly int baseVal = 31;
private int[] hash;
private int[] power;
// modular addition
private int Add(int a, int b) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
private int Sub(int a, int b) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
private int Mul(int a, int b) {
return (int)((1L * a * b) % mod);
}
// convert character to int
// ('a' = 1, ..., 'z' = 26)
private int CharToInt(char c) {
return c - 'a' + 1;
}
// constructor: precomputes prefix hashes and powers
public RabinKarpHash(string s) {
int n = s.Length;
hash = new int[n];
power = new int[n];
hash[0] = CharToInt(s[0]);
power[0] = 1;
for (int i = 1; i < n; ++i) {
hash[i] = Add(Mul(hash[i - 1], baseVal),
CharToInt(s[i]));
power[i] = Mul(power[i - 1], baseVal);
}
}
// get hash of substring s[l...r] in O(1)
public int GetSubHash(int l, int r) {
int h = hash[r];
if (l > 0) {
h = Sub(h, Mul(hash[l - 1], power[r - l + 1]));
}
return h;
}
}
class GfG {
// Rabin-Karp search using hash class
public static List<int> SearchPattern
(string text, string pattern) {
int n = text.Length, m = pattern.Length;
RabinKarpHash textHash = new RabinKarpHash(text);
RabinKarpHash patHash = new RabinKarpHash(pattern);
int patternHash = patHash.GetSubHash(0, m - 1);
List<int> result = new List<int>();
for (int i = 0; i <= n - m; i++) {
int subHash = textHash.GetSubHash(i, i + m - 1);
if (subHash == patternHash) {
result.Add(i);
}
}
return result;
}
public static void Main() {
string txt = "geeksforgeeks";
string pat = "geek";
List<int> positions = SearchPattern(txt, pat);
foreach (int idx in positions) {
Console.Write(idx + " ");
}
Console.WriteLine();
}
}
class RabinKarpHash {
constructor(s) {
this.mod = 1e9 + 7;
this.base = 31;
this.hash = new Array(s.length);
this.power = new Array(s.length);
// convert character to int
// ('a' = 1, ..., 'z' = 26)
const charToInt = c => c.charCodeAt(0) - 'a'.charCodeAt(0) + 1;
this.hash[0] = charToInt(s[0]);
this.power[0] = 1;
for (let i = 1; i < s.length; i++) {
this.hash[i] = (this.hash[i - 1] * this.base
+ charToInt(s[i])) % this.mod;
this.power[i] = (this.power[i - 1] * this.base) % this.mod;
}
}
// get hash of substring s[l...r] in O(1)
getSubHash(l, r) {
let h = this.hash[r];
if (l > 0) {
h = (h - this.hash[l - 1] * this.power[r - l + 1]) % this.mod;
if (h < 0) h += this.mod;
}
return h;
}
}
// Rabin-Karp search using hash class
function searchPattern(text, pattern) {
let n = text.length, m = pattern.length;
let textHash = new RabinKarpHash(text);
let patHash = new RabinKarpHash(pattern);
let patternHash = patHash.getSubHash(0, m - 1);
let result = [];
for (let i = 0; i <= n - m; i++) {
let subHash = textHash.getSubHash(i, i + m - 1);
if (subHash === patternHash) {
result.push(i);
}
}
return result;
}
// Driver Code
let txt = "geeksforgeeks";
let pat = "geek";
let positions = searchPattern(txt, pat);
console.log(positions.join(" "));
Output
0 8
Time Complexity: O(n + m), we compute prefix hashes and powers for both text and pattern in O(n + m). Then, we slide a window over the text, and each substring hash is compared in O(1).
Auxiliary Space: O(n + m) ,we store prefix hashes and power arrays for both text and pattern, taking O(n + m) space.
Limitations of Rabin-Karp
- Hash collisions may occur — different substrings can have the same hash.
- Requires character-by-character check to confirm matches.
- Risk of modulo overflow if not handled with care.
- Performance depends on good hash function and prime modulus.
- Slightly higher constant factors compared to simpler algorithms like KMP.
Why Single Hash Can Fail (Hash Collisions):
When using a single hash function, there's always a chance that two different substrings may produce the same hash value. This is called a hash collision.
Why does it happen?
=> We're computing hashes modulo a large number (e.g., 10^9 + 7)
=> But since the number of possible substrings is huge, different substrings might accidentally result in the same hash after taking the modulo.
Consequence: If two different substrings have the same hash, the algorithm may falsely report a match (false positive). Rabin-Karp, in such a case, needs to verify the actual characters to confirm a match — which slows down performance.
Need for Double Hashing
To reduce the probability of collisions, we use double hashing — i.e., compute two independent hashes with different: Base values (p1, p2) and Moduli (mod1, mod2)
How it helps:
=> Now, two substrings are considered equal only if both hash values match.
=> The probability of two different substrings colliding in both hash functions is extremely low — roughly 1/(mod1 x mod2), which is practically negligible.
#include <iostream>
#include <vector>
#include <string>
using namespace std;
class RabinKarpHash {
private:
const int mod1 = 1e9 + 7;
const int mod2 = 1e9 + 9;
const int base1 = 31;
const int base2 = 37;
vector<int> hash1, hash2;
vector<int> power1, power2;
// modular addition
int add(int a, int b, int mod) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
int sub(int a, int b, int mod) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
int mul(int a, int b, int mod) {
return (int)((1LL * a * b) % mod);
}
// convert character to int
int charToInt(char c) {
return c - 'a' + 1;
}
public:
// constructor: precomputes both prefix hashes and powers
RabinKarpDoubleHash(string &s) {
int n = s.size();
hash1.resize(n);
hash2.resize(n);
power1.resize(n);
power2.resize(n);
hash1[0] = charToInt(s[0]);
hash2[0] = charToInt(s[0]);
power1[0] = 1;
power2[0] = 1;
for (int i = 1; i < n; ++i) {
hash1[i] = add(mul(hash1[i - 1], base1, mod1),
charToInt(s[i]), mod1);
power1[i] = mul(power1[i - 1], base1, mod1);
hash2[i] = add(mul(hash2[i - 1], base2, mod2),
charToInt(s[i]), mod2);
power2[i] = mul(power2[i - 1], base2, mod2);
}
}
// get double hash of substring s[l...r]
vector<int> getSubHash(int l, int r) {
int h1 = hash1[r];
int h2 = hash2[r];
if (l > 0) {
h1 = sub(h1, mul(hash1[l - 1], power1[r - l + 1], mod1), mod1);
h2 = sub(h2, mul(hash2[l - 1], power2[r - l + 1], mod2), mod2);
}
return {h1, h2};
}
};
import java.util.ArrayList;
public class RabinKarpHash {
private final int mod1 = (int) 1e9 + 7;
private final int mod2 = (int) 1e9 + 9;
private final int base1 = 31;
private final int base2 = 37;
private int[] hash1, hash2;
private int[] power1, power2;
// modular addition
private int add(int a, int b, int mod) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
private int sub(int a, int b, int mod) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
private int mul(int a, int b, int mod) {
return (int) ((1L * a * b) % mod);
}
// convert character to int
private int charToInt(char c) {
return c - 'a' + 1;
}
// constructor: precomputes both prefix hashes and powers
public RabinKarpHash(String s) {
int n = s.length();
hash1 = new int[n];
hash2 = new int[n];
power1 = new int[n];
power2 = new int[n];
hash1[0] = charToInt(s.charAt(0));
hash2[0] = charToInt(s.charAt(0));
power1[0] = 1;
power2[0] = 1;
for (int i = 1; i < n; ++i) {
hash1[i] = add(mul(hash1[i - 1], base1, mod1),
charToInt(s.charAt(i)), mod1);
power1[i] = mul(power1[i - 1], base1, mod1);
hash2[i] = add(mul(hash2[i - 1], base2, mod2),
charToInt(s.charAt(i)), mod2);
power2[i] = mul(power2[i - 1], base2, mod2);
}
}
// get double hash of substring s[l...r]
public ArrayList<Integer> getSubHash(int l, int r) {
int h1 = hash1[r];
int h2 = hash2[r];
if (l > 0) {
h1 = sub(h1, mul(hash1[l - 1], power1[r - l + 1], mod1), mod1);
h2 = sub(h2, mul(hash2[l - 1], power2[r - l + 1], mod2), mod2);
}
ArrayList<Integer> res = new ArrayList<>();
res.add(h1);
res.add(h2);
return res;
}
}
class RabinKarpHash:
def __init__(self, s):
self.mod1 = int(1e9) + 7
self.mod2 = int(1e9) + 9
self.base1 = 31
self.base2 = 37
n = len(s)
self.hash1 = [0] * n
self.hash2 = [0] * n
self.power1 = [0] * n
self.power2 = [0] * n
self.hash1[0] = self.charToInt(s[0])
self.hash2[0] = self.charToInt(s[0])
self.power1[0] = 1
self.power2[0] = 1
for i in range(1, n):
self.hash1[i] = self.add(self.mul(self.hash1[i - 1], self.base1, self.mod1),
self.charToInt(s[i]), self.mod1)
self.power1[i] = self.mul(self.power1[i - 1], self.base1, self.mod1)
self.hash2[i] = self.add(self.mul(self.hash2[i - 1], self.base2, self.mod2),
self.charToInt(s[i]), self.mod2)
self.power2[i] = self.mul(self.power2[i - 1], self.base2, self.mod2)
def charToInt(self, c):
return ord(c) - ord('a') + 1
def add(self, a, b, mod):
a += b
if a >= mod:
a -= mod
return a
def sub(self, a, b, mod):
a -= b
if a < 0:
a += mod
return a
def mul(self, a, b, mod):
return (a * b) % mod
def getSubHash(self, l, r):
h1 = self.hash1[r]
h2 = self.hash2[r]
if l > 0:
h1 = self.sub(h1, self.mul(self.hash1[l - 1], \
self.power1[r - l + 1], self.mod1), self.mod1)
h2 = self.sub(h2, self.mul(self.hash2[l - 1], \
self.power2[r - l + 1], self.mod2), self.mod2)
return [h1, h2]
using System;
using System.Collections.Generic;
class RabinKarpHash{
private int mod1 = (int)1e9 + 7;
private int mod2 = (int)1e9 + 9;
private int base1 = 31;
private int base2 = 37;
private int[] hash1, hash2, power1, power2;
// modular addition
private int add(int a, int b, int mod) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
private int sub(int a, int b, int mod) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
private int mul(int a, int b, int mod) {
return (int)((1L * a * b) % mod);
}
// convert character to int
private int charToInt(char c) {
return c - 'a' + 1;
}
// constructor: precomputes both prefix hashes and powers
public GfG(string s) {
int n = s.Length;
hash1 = new int[n];
hash2 = new int[n];
power1 = new int[n];
power2 = new int[n];
hash1[0] = charToInt(s[0]);
hash2[0] = charToInt(s[0]);
power1[0] = 1;
power2[0] = 1;
for (int i = 1; i < n; i++) {
hash1[i] = add(mul(hash1[i - 1], base1, mod1),
charToInt(s[i]), mod1);
power1[i] = mul(power1[i - 1], base1, mod1);
hash2[i] = add(mul(hash2[i - 1], base2, mod2),
charToInt(s[i]), mod2);
power2[i] = mul(power2[i - 1], base2, mod2);
}
}
// get double hash of substring s[l...r]
public List<int> getSubHash(int l, int r) {
int h1 = hash1[r];
int h2 = hash2[r];
if (l > 0) {
h1 = sub(h1, mul(hash1[l - 1], power1[r - l + 1], mod1), mod1);
h2 = sub(h2, mul(hash2[l - 1], power2[r - l + 1], mod2), mod2);
}
return new List<int> { h1, h2 };
}
}
class RabinKarpDoubleHash {
constructor(s) {
this.mod1 = 1e9 + 7;
this.mod2 = 1e9 + 9;
this.base1 = 31;
this.base2 = 37;
const n = s.length;
this.hash1 = Array(n);
this.hash2 = Array(n);
this.power1 = Array(n);
this.power2 = Array(n);
this.hash1[0] = this.charToInt(s[0]);
this.hash2[0] = this.charToInt(s[0]);
this.power1[0] = 1;
this.power2[0] = 1;
for (let i = 1; i < n; i++) {
this.hash1[i] = this.add(
this.mul(this.hash1[i - 1], this.base1, this.mod1),
this.charToInt(s[i]), this.mod1
);
this.power1[i] = this.mul(this.power1[i - 1],
this.base1, this.mod1);
this.hash2[i] = this.add(
this.mul(this.hash2[i - 1], this.base2, this.mod2),
this.charToInt(s[i]), this.mod2
);
this.power2[i] = this.mul(this.power2[i - 1],
this.base2, this.mod2);
}
}
// convert character to int
charToInt(c) {
return c.charCodeAt(0) - 'a'.charCodeAt(0) + 1;
}
// modular addition
add(a, b, mod) {
a += b;
if (a >= mod) a -= mod;
return a;
}
// modular subtraction
sub(a, b, mod) {
a -= b;
if (a < 0) a += mod;
return a;
}
// modular multiplication
mul(a, b, mod) {
return Math.floor((a * b) % mod);
}
// get double hash of substring s[l...r]
getSubHash(l, r) {
let h1 = this.hash1[r];
let h2 = this.hash2[r];
if (l > 0) {
h1 = this.sub(h1, this.mul(this.hash1[l - 1],
this.power1[r - l + 1], this.mod1), this.mod1);
h2 = this.sub(h2, this.mul(this.hash2[l - 1],
this.power2[r - l + 1], this.mod2), this.mod2);
}
return [h1, h2];
}
}
Time Complexity: O(n), the prefix hashes and powers are precomputed in a single pass over the string, which takes linear time. Once built, any substring hash can be retrieved in O(1) time.
Auxiliary Space: O(n), two arrays of size n are used to store the prefix hashes and powers of the base, resulting in linear extra space usage.
Types of Problems Rabin-Karp Can Solve
- Pattern matching – Find all occurrences of a pattern in a large text
- Plagiarism detection – Compare documents by checking for common substrings
- Multiple pattern search – Efficiently search for several patterns at once
- Substring comparison – Quickly compare substrings using hashes
- Palindrome and DP problems – Used for hashing-based optimizations
- Detect duplicate substrings – Find repeated sequences in strings
- Longest common prefix/suffix – In constant time using precomputed hashes