Laplace-Verteilung

Dichtefunktionen der Laplace-Verteilung für unterschiedliche Parameter

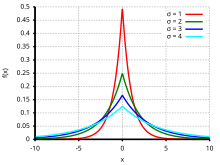
Die Laplace-Verteilung (benannt nach Pierre-Simon Laplace, einem französischen Mathematiker und Astronomen) ist eine stetige Wahrscheinlichkeitsverteilung. Da sie die Form zweier aneinandergefügter Exponentialverteilungen hat, wird sie auch als Doppelexponentialverteilung oder zweiseitige Exponentialverteilung bezeichnet.

Definition

Eine stetige Zufallsgröße $X$ unterliegt der Laplace-Verteilung mit dem Lageparameter $\mu \in \mathbb {R}$ und dem Skalenparameter $\sigma >0$, wenn sie die Wahrscheinlichkeitsdichte

$f(x)={\frac {1}{2\sigma }}e^{\displaystyle -{\frac {\left|x-\mu \right|}{\sigma }}}$

besitzt.

Ihre Verteilungsfunktion lautet

$F(x)={\begin{cases}\displaystyle {1 \over 2}e^{\displaystyle {\frac {x-\mu }{\sigma }}},&x\leq \mu \\\displaystyle 1-{1 \over 2}e^{\displaystyle -{\frac {x-\mu }{\sigma }}}&x>\mu \end{cases}}$

Mittels der Signum-Funktion lässt sie sich geschlossen darstellen als

$F(x)={\tfrac {1}{2}}+{\tfrac {1}{2}}\operatorname {sgn} \left(x-\mu \right)\left(1-\exp \left(-{\frac {\left|x-\mu \right|}{\sigma }}\right)\right)$.

Eigenschaften

Symmetrie

Die Wahrscheinlichkeitsdichte ist achsensymmetrisch zur Geraden $x=\mu$ und die Verteilungsfunktion ist punktsymmetrisch zum Punkt $(\mu ,1/2)$.

Erwartungswert, Median, Modalwert

Der Parameter $\mu$ ist gleichzeitig Erwartungswert, Median und Modalwert.

$\operatorname {E} (X)=\mu$

Varianz

Die Varianz wird durch den Parameter $\sigma$ bestimmt.

$\operatorname {Var} (X)=2\sigma ^{2}$

Schiefe

Die Schiefe der Laplace-Verteilung ist

$\operatorname {v} (X)=0$.

Kurtosis

Die Wölbung einer Laplace-Verteilung ist identisch 6 (entspricht einem Exzess von 3).

$\operatorname {Kurt} (X)=6$

Kumulanten

Alle Kumulante $\kappa _{k}$ mit ungeradem Grad $k>2$ sind gleich Null. Für gerade $k$ gilt

$\kappa _{k}=2(k-1)!\sigma ^{k}$

Momenterzeugende Funktion

Die momenterzeugende Funktion eine Laplace-verteilten Zufallsgröße mit Parametern $\mu$ und $\sigma$ lautet

$M_{X}(t)={\frac {e^{\mu t}}{1-\sigma ^{2}t^{2}}}$, für $|t|<1/\sigma .$

Charakteristische Funktion

Die charakteristische Funktion entsteht aus der momenterzeugenden Funktion, indem man das Argument $t$ durch $is$ ersetzt, man erhält:

$\phi _{X}(s)={\frac {e^{i\mu s}}{1+\sigma ^{2}s^{2}}}$.

Entropie

Die Entropie der Laplace-Verteilung (ausgedrückt in nats) beträgt

$1+\ln(2\sigma )$.

Zufallszahlen

Zur Erzeugung doppelexponentialverteilter Zufallszahlen bietet sich die Inversionsmethode an.

Die nach dem Simulationslemma zu bildende Pseudoinverse der Verteilungsfunktion lautet hierbei

$F^{-1}(y)={\begin{cases}\displaystyle {1 \over \lambda }\ln(2y)&y<{1 \over 2}\\\displaystyle -{1 \over \lambda }\ln(2(1-y)),&y\geq {1 \over 2}\end{cases}}$.

Zu einer Folge von Standardzufallszahlen $u_{i}$ lässt sich daher eine Folge

$x_{i}:=F^{-1}(u_{i})$

doppelexponentialverteilter Zufallszahlen berechnen.

Beziehung zu anderen Verteilungen

Beziehung zur Normalverteilung

Sind $X_{1},X_{2},X_{3},X_{4}\sim {\mathcal {N}}(0,1)$ unabhängige standardnormalverteilte Zufallsgrößen, dann ist $Z=\det {\begin{pmatrix}X_{1}&X_{2}\\X_{3}&X_{4}\end{pmatrix}}=X_{1}\,X_{4}-X_{2}\,X_{3}$ standardlaplaceverteilt ($\mu =0$).

Beziehung zur Exponentialverteilung

Eine Zufallsvariable $X:=Y_{\lambda }-Z_{\lambda }$, die als Differenz zweier unabhängiger exponentialverteilter Zufallsvariablen $Y_{\lambda }$ und $Z_{\lambda }$ mit demselben Parameter definiert ist, ist Laplace-verteilt.

Beziehung zur Rademacher-Verteilung

Ist $X$ Rademacher-Verteilt, und ist $Y$ Exponentialverteilt zum Parameter $\lambda$, so ist $X\cdot Y$Laplace-Verteilt zu dem Lageparameter 0 und dem Skalenparametern ${\frac {1}{\lambda }}$.

Abgrenzung zur stetigen Gleichverteilung

Die so definierte stetige Laplaceverteilung hat nichts mit der stetigen Gleichverteilung zu tun. Sie wird mit ihr trotzdem gerne verwechselt, weil die diskrete Gleichverteilung nach Laplace benannt ist (Laplacewürfel)

Quellen

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | Dirac | diskret uniform | empirisch | hypergeometrisch | kategorial | negativ hypergeometrisch | Rademacher | verallgemeinert binomial | Zipf | Zipf-Mandelbrot | Zweipunkt

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | discrete-Phase-Type | erweitert negativ binomial | Gauss-Kuzmin | gemischt Poisson | geometrisch | logarithmisch | negativ binomial | parabolisch-fraktal | Poisson | Skellam | verallgemeinert Poisson | Yule-Simon | Zeta

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Cantor | Kumaraswamy | raised Cosine | Dreieck | Trapez | U-quadratisch | stetig uniform | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi | Chi-Quadrat | Coxian | Erlang | Exponential | Extremwert | F | Fermi-Dirac | Folded normal | Fréchet | Gamma | Gamma-Gamma | verallgemeinert invers Gauß | halblogistisch | halbnormal | Hartman-Watson | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | invers Chi-Quadrat | scale-invers Chi-Quadrat | Invers Normal | Invers Gamma | Kolmogorow-Verteilung | Lévy | log-normal | log-logistisch | Maxwell-Boltzmann | Maxwell-Speed | Nakagami | nichtzentriert Chi-Quadrat | Pareto | Phase-Type | Rayleigh | relativistisch Breit-Wigner | Rice | Rosin-Rammler | shifted Gompertz | truncated normal | Type-2-Gumbel | Weibull | Wilks’ Lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | exponential Power | Fishers z | Fisher-Tippett (Gumbel) | generalized hyperbolic | Hyperbolic-secant | Landau | Laplace | alpha-stabil | logistisch | normal (Gauß) | normal-invers Gauß’sch | Skew-normal | Studentsche t | Type-1-Gumbel | Variance-Gamma | Voigt

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Dirichlet compound multinomial | Ewens | gemischt Multinomial | multinomial | multivariat hypergeometrisch | multivariat Poisson | negativmultinomial | Pólya/Eggenberger | polyhypergeometrisch

Kontinuierliche multivariate Verteilungen:
Dirichlet | GEM | generalized Dirichlet | multivariat normal | multivariat Student | normalskaliert invers Gamma | Normal-Gamma | Poisson-Dirichlet

Multivariate Matrixverteilungen:
Gleichverteilung auf der Stiefel-Mannigfaltigkeit | Invers Wishart | Matrix Beta | Matrix Gamma | Matrix invers Beta | Matrix invers Gamma | Matrix Normal | Matrix Student-t | Matrix-Von-Mises-Fisher-Verteilung | Normal-invers-Wishart | Normal-Wishart | Wishart