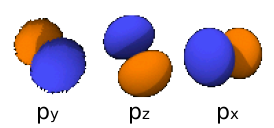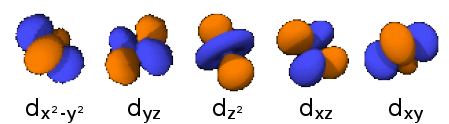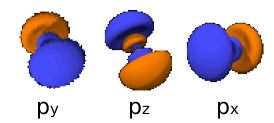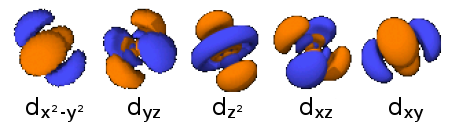Χημεία, μ みゅー ι いおた α あるふぁ κ かっぱ α あるふぁ ι いおた [ επεξεργασία ] Η いーた κ かっぱ α あるふぁ ι いおた τ たう ο おみくろん [ επεξεργασία ] Φάσματα κ かっぱ α あるふぁ ι いおた [ επεξεργασία ] Δυαδική φύση τ たう ο おみくろん υ うぷしろん [ επεξεργασία ] Επί πολλούς αιώνες τ たう ο おみくろん φως κ かっぱ α あるふぁ ι いおた η いーた τ たう ο おみくろん υ うぷしろん κ かっぱ α あるふぁ ι いおた τ たう ο おみくろん ν にゅー 17ο おみくろん , η いーた τ たう ω おめが ν にゅー τ たう ο おみくろん υ うぷしろん Ισαάκ Νεύτων κ かっぱ α あるふぁ ι いおた τ たう ο おみくろん υ うぷしろん Κρίστιαν Χόυχενς . Είναι ροή υλικών σωματιδίων ή κύμα = ενέργεια ; Διαδίδεται ευθύγραμμα, ανακλάται , διαθλάται , μεταδίδει ορμή σ しぐま ε いぷしろん σώματα πάνω σ しぐま τ たう α あるふぁ σ しぐま α あるふぁ ν にゅー κ かっぱ α あるふぁ ι いおた φαινόμενα περίθλασης κ かっぱ α あるふぁ ι いおた συμβολής , σ しぐま α あるふぁ ν にゅー Τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん ηλεκτρομαγνητικού φάσματος , π ぱい ο おみくろん υ うぷしろん ακτίνες Χ かい , τ たう η いーた ν にゅー υπέρυθρη κ かっぱ α あるふぁ ι いおた τ たう η いーた ν にゅー υπεριώδη ακτινοβολία .Η いーた ταχύτητα τ たう ο おみくろん υ うぷしろん σ しぐま τ たう ο おみくろん
c
≃
3
⋅
10
8
m
/
s
{\displaystyle c\simeq 3\cdot 10^{8}\;m/s}
τ たう η いーた συχνότητά τ たう ο おみくろん υ うぷしろん τ たう ο おみくろん μήκος κύματός τ たう ο おみくろん υ うぷしろん λ らむだ
Από τ たう α あるふぁ τ たう ο おみくろん υ うぷしろん 19ο おみくろん υ うぷしろん παρατηρήθηκε τ たう ο おみくろん φωτοηλεκτρικό φαινόμενο », δηλαδή τ たう ο おみくろん ν にゅー α あるふぁ ηλεκτρόνια από μέταλλα όταν πέφτει πάνω σ しぐま μ みゅー ε いぷしろん κ かっぱ α あるふぁ ι いおた η いーた κ かっぱ α あるふぁ ι いおた τ たう η いーた ν にゅー ένταση της φωτεινής ακτινοβολίας.
Τ たう ο おみくろん 1905 ο おみくろん Άλμπερτ Αϊνστάιν επέκτεινε τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん Μ みゅー α あるふぁ ξ くしー Π ぱい λ らむだ α あるふぁ ν にゅー κ かっぱ τ たう η いーた ν にゅー «κβαντισμένη» , δηλαδή αποτελούμενη από διακριτά τμήματα π ぱい ο おみくろん υ うぷしろん «κβάντα» . Σ しぐま τ たう α あるふぁ τ たう ο おみくろん φωτόνια ». Διατύπωσε λοιπόν τ たう η いーた ν にゅー
E
=
h
v
{\displaystyle E=hv}
όπου:
Ε いぷしろん
h
=
6
,
6
⋅
10
−
34
J
s
:
{\displaystyle h=6,6\cdot 10^{-34}\;Js:}
τ たう ο おみくろん υ うぷしろん v : συχνότητα ηλεκτρομαγνητικής ενέργειας. Η いーた κ かっぱ α あるふぁ ι いおた τ たう ω おめが ν にゅー δ でるた υ うぷしろん ο おみくろん «σχέση Planck - Einstein» . Η いーた τ たう ο おみくろん υ うぷしろん μ みゅー ε いぷしろん Η いーた κινητική ενέργεια κάθε αποσπούμενου ηλεκτρονίου δίνεται από τ たう η いーた ν にゅー
h
v
=
A
+
1
2
m
υ うぷしろん
2
{\displaystyle hv=A+{\frac {1}{2}}m\upsilon ^{2}}
όπου:
h
=
6
,
6
⋅
10
−
34
J
s
:
{\displaystyle h=6,6\cdot 10^{-34}\;Js:}
τ たう ο おみくろん υ うぷしろん v : συχνότητα ηλεκτρομαγνητικής ενέργειας.
Α あるふぁ π ぱい ο おみくろん υ うぷしろん
m
=
m
e
=
9
,
1
⋅
10
−
31
m
:
{\displaystyle m=m_{e}=9,1\cdot 10^{-31}\;m:}
υ うぷしろん Γ がんま ι いおた α あるふぁ μ みゅー ε いぷしろん 0 η いーた τ たう η いーた ν にゅー
p
=
E
2
−
m
0
2
c
4
c
{\displaystyle p={\frac {\sqrt {E^{2}-{m_{0}}^{2}c^{4}}}{c}}}
όπου:
p: η いーた
E: η いーた
m0 : μάζα ηρεμίας τ たう ο おみくろん υ うぷしろん
c
=
3
⋅
10
8
m
/
s
:
{\displaystyle c=3\cdot 10^{8}\;m/s:}
Η いーた τ たう ο おみくろん υ うぷしろん σ しぐま τ たう ο おみくろん Γ がんま ι いおた α あるふぁ γ がんま ι いおた α あるふぁ τ たう ο おみくろん 0 = 0, η いーた
p
=
E
c
=
h
v
c
=
h
λ らむだ
{\displaystyle p={\frac {E}{c}}={\frac {hv}{c}}={\frac {h}{\lambda }}}
όπου:
p: η いーた
E: η いーた
c
=
3
⋅
10
8
m
/
s
:
{\displaystyle c=3\cdot 10^{8}\;m/s:}
Η いーた τ たう ο おみくろん υ うぷしろん σ しぐま τ たう ο おみくろん
h
=
6
,
6
⋅
10
−
34
J
s
:
{\displaystyle h=6,6\cdot 10^{-34}\;Js:}
τ たう ο おみくろん υ うぷしろん v : συχνότητα ηλεκτρομαγνητικής ενέργειας.
λ らむだ Η いーた «σχέση υλοκυμάτων τ たう ο おみくろん υ うぷしろん . Μ みゅー ε いぷしろん κ かっぱ α あるふぁ ι いおた κ かっぱ α あるふぁ ι いおた σ しぐま τ たう η いーた ν にゅー κ かっぱ α あるふぁ ι いおた σ しぐま τ たう α あるふぁ
Κυματική φύση τ たう ο おみくろん υ うぷしろん [ επεξεργασία ] Η いーた [ επεξεργασία ] Η いーた σ しぐま ε いぷしろん π ぱい χ かい «Δύναμη ονομάζεται ο おみくろん , ή μαθηματικά:
F
→
=
d
p
→
d
t
{\displaystyle {\vec {F}}={\frac {d{\vec {p}}}{dt}}}
όπου:
F
→
{\displaystyle {\vec {F}}}
η いーた
p
→
{\displaystyle {\vec {p}}}
η いーた t: ο おみくろん Είναι ένα αξίωμα π ぱい ο おみくろん υ うぷしろん σ しぐま τ たう α あるふぁ υλικά σώμτα τ たう ο おみくろん υ うぷしろん μακρόκοσμου , αλλά δ でるた ε いぷしろん ν にゅー ν にゅー α あるふぁ μ みゅー ε いぷしろん σ しぐま τ たう α あるふぁ υλοκύματα τ たう ο おみくろん υ うぷしろん μικροκόσμου . Βασικό κριτήριο εφαρμογής ή μ みゅー η いーた η いーた μ みゅー ε いぷしろん τ たう α あるふぁ Γ がんま ι いおた α あるふぁ τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん θ しーた α あるふぁ ν にゅー α あるふぁ δ でるた υ うぷしろん ο おみくろん
1. Ν にゅー α あるふぁ τ たう η いーた ν にゅー τ たう η いーた ν にゅー ν にゅー α あるふぁ π ぱい ο おみくろん υ うぷしろん ν にゅー α あるふぁ τ たう α あるふぁ
2. Ν にゅー α あるふぁ τ たう α あるふぁ τ たう ω おめが ν にゅー ν にゅー α あるふぁ π ぱい ο おみくろん υ うぷしろん ν にゅー α あるふぁ τ たう α あるふぁ Ο おみくろん π ぱい ι いおた ο おみくろん κ かっぱ α あるふぁ ι いおた θ しーた α あるふぁ τ たう ο おみくろん ν にゅー Σ しぐま ε いぷしろん τ たう α あるふぁ π ぱい ο おみくろん υ うぷしろん γ がんま ι いおた α あるふぁ τ たう η いーた ν にゅー α あるふぁ π ぱい μ みゅー ι いおた α あるふぁ κυματική εξίσωση , όπως αυτή π ぱい ο おみくろん υ うぷしろん δ でるた ε いぷしろん ν にゅー ο おみくろん χρόνος , αλλά περισσότερα τ たう α あるふぁ σ しぐま τ たう α あるふぁ Σ しぐま τ たう η いーた δ でるた ε いぷしろん τ たう ο おみくろん τ たう α あるふぁ τ たう η いーた ν にゅー τ たう ω おめが ν にゅー κ かっぱ α あるふぁ ι いおた τ たう η いーた ν にゅー τ たう ω おめが ν にゅー κ かっぱ α あるふぁ ι いおた τ たう ω おめが ν にゅー κ かっぱ α あるふぁ ι いおた σ しぐま τ たう η いーた τ たう ω おめが ν にゅー τ たう η いーた ν にゅー β べーた λ らむだ ν にゅー α あるふぁ μ みゅー ι いおた α あるふぁ τ たう η いーた ν にゅー γ がんま ι いおた α あるふぁ σ しぐま ε いぷしろん μ みゅー ι いおた α あるふぁ σ しぐま τ たう ο おみくろん ν にゅー
y
(
x
)
=
A
η いーた μ みゅー
2
π ぱい x
λ らむだ
{\displaystyle y{\begin{pmatrix}x\end{pmatrix}}=A\eta \mu {\frac {2\pi x}{\lambda }}}
όπου:
y
(
x
)
{\displaystyle y{\begin{pmatrix}x\end{pmatrix}}}
τ たう ο おみくろん x: τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん
A: τ たう ο おみくろん
η いーた μ みゅー
2
π ぱい x
λ らむだ
=
1
{\displaystyle \eta \mu {\frac {2\pi x}{\lambda }}=1}
Σημειώστε ότι σ しぐま τ たう η いーた ν にゅー η いーた τ たう ο おみくろん υ うぷしろん μ みゅー ε いぷしろん
y
(
0
)
=
0
{\displaystyle y{\begin{pmatrix}0\end{pmatrix}}=0}
Τώρα παραγωγίζουμε δ でるた υ うぷしろん ο おみくろん τ たう η いーた ν にゅー
d
2
y
d
x
2
=
−
4
π ぱい
2
A
λ らむだ
2
η いーた μ みゅー
2
π ぱい x
λ らむだ
⇔
d
2
y
d
x
2
=
−
4
π ぱい
2
λ らむだ
2
y
{\displaystyle {\frac {d^{2}y}{dx^{2}}}=-{\frac {4\pi ^{2}A}{\lambda ^{2}}}\eta \mu {\frac {2\pi x}{\lambda }}\Leftrightarrow {\frac {d^{2}y}{dx^{2}}}=-{\frac {4\pi ^{2}}{\lambda ^{2}}}y}
Η いーた δ でるた ε いぷしろん γ がんま ι いおた α あるふぁ τ たう ο おみくろん Α あるふぁ τ たう ο おみくろん λ らむだ τ たう η いーた ν にゅー π ぱい ο おみくろん υ うぷしろん κ かっぱ ι いおた δ でるた ε いぷしろん ν にゅー μ みゅー ι いおた α あるふぁ τ たう η いーた ν にゅー α あるふぁ ν にゅー η いーた
y
(
x
)
=
A
η いーた μ みゅー
[
2
π ぱい
λ らむだ
(
x
+
ϕ
)
]
{\displaystyle y{\begin{pmatrix}x\end{pmatrix}}=A\eta \mu {\begin{bmatrix}{\frac {2\pi }{\lambda }}{\begin{pmatrix}x+\phi \end{pmatrix}}\end{bmatrix}}}
όπου:
φ ふぁい Μπορούμε ν にゅー α あるふぁ τ たう η いーた ν にゅー π ぱい ο おみくろん υ うぷしろん
y
(
0
)
=
0
{\displaystyle y{\begin{pmatrix}0\end{pmatrix}}=0}
η いーた
A
η いーた μ みゅー
[
2
π ぱい
λ らむだ
(
0
+
ϕ
)
]
⇔
ϕ
=
0
{\displaystyle A\eta \mu {\begin{bmatrix}{\frac {2\pi }{\lambda }}{\begin{pmatrix}0+\phi \end{pmatrix}}\end{bmatrix}}\Leftrightarrow \phi =0}
.
Έτσι ξανακαταλήγουμε όμως σ しぐま τ たう η いーた ν にゅー
y
(
x
)
=
A
η いーた μ みゅー
2
π ぱい x
λ らむだ
{\displaystyle y{\begin{pmatrix}x\end{pmatrix}}=A\eta \mu {\frac {2\pi x}{\lambda }}}
Ακόμη, μπορούμε ν にゅー α あるふぁ κ かっぱ ι いおた σ しぐま ε いぷしろん
ℓ
{\displaystyle \ell }
y
(
ℓ
)
=
0
{\displaystyle y{\begin{pmatrix}\ell \end{pmatrix}}=0}
Σ しぐま τ たう η いーた ν にゅー
y
(
ℓ
)
=
A
η いーた μ みゅー
2
π ぱい ℓ
λ らむだ
=
0
⇔
2
π ぱい ℓ
λ らむだ
=
n
π ぱい ⇔
λ らむだ =
2
ℓ
n
{\displaystyle y{\begin{pmatrix}\ell \end{pmatrix}}=A\eta \mu {\frac {2\pi \ell }{\lambda }}=0\Leftrightarrow {\frac {2\pi \ell }{\lambda }}=n\pi \Leftrightarrow \lambda ={\frac {2\ell }{n}}}
.
όπου:
n: ακέραιος αριθμός. Ξεκινώντας δηλαδή από μ みゅー ι いおた α あるふぁ γ がんま ι いおた α あるふぁ μ みゅー ε いぷしろん τ たう η いーた σ しぐま τ たう η いーた ν にゅー κβάνγτωση κ かっぱ α あるふぁ ι いおた σ しぐま τ たう ο おみくろん ν にゅー κύριο κβαντικό αριθμό n . Η いーた γ がんま ι いおた α あるふぁ τ たう α あるふぁ α あるふぁ π ぱい τ たう ο おみくろん μ みゅー ε いぷしろん τ たう ο おみくろん ψ ぷさい τ たう η いーた γ がんま ι いおた α あるふぁ ν にゅー α あるふぁ τ たう ο おみくろん λ らむだ μ みゅー ε いぷしろん τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん σ しぐま τ たう ο おみくろん ν にゅー x ). Έτσι παίρνουμε τ たう η いーた ν にゅー
d
2
ψ ぷさい
d
x
2
=
−
4
π ぱい
2
h
2
p
x
2
ψ ぷさい
{\displaystyle {\frac {d^{2}\psi }{dx^{2}}}=-{\frac {4\pi ^{2}}{h^{2}}}{p_{x}}^{2}\psi }
.
Όμως η いーた δ でるた ε いぷしろん ν にゅー δ でるた ε いぷしろん ν にゅー τ たう η いーた ν にゅー σ しぐま τ たう ο おみくろん π ぱい ο おみくろん υ うぷしろん σ しぐま ε いぷしろん μ みゅー ι いおた α あるふぁ Ο おみくろん γ がんま ι いおた α あるふぁ ν にゅー α あるふぁ τ たう η いーた ν にゅー α あるふぁ τ たう ο おみくろん π ぱい ο おみくろん υ うぷしろん τ たう η いーた ν にゅー Η いーた τ たう ο おみくろん υ うぷしろん μ みゅー ε いぷしろん τ たう η いーた ν にゅー ν にゅー ε いぷしろん τ たう η いーた ν にゅー
T
=
1
2
m
υ うぷしろん
2
=
p
2
2
m
{\displaystyle T={\frac {1}{2}}m\upsilon ^{2}={\frac {p^{2}}{2m}}}
.
όπου:
m: η いーた τ たう ο おみくろん υ うぷしろん Αλλά η いーた Τ たう η いーた τ たう η いーた ν にゅー Ε いぷしろん
T
=
E
−
V
(
x
)
⇔
p
x
2
2
m
=
E
−
V
(
x
)
⇔
p
x
2
=
2
m
[
E
−
V
(
x
)
]
{\displaystyle T=E-V{\begin{pmatrix}x\end{pmatrix}}\Leftrightarrow {\frac {{p_{x}}^{2}}{2m}}=E-V{\begin{pmatrix}x\end{pmatrix}}\Leftrightarrow {p_{x}}^{2}=2m{\begin{bmatrix}E-V{\begin{pmatrix}x\end{pmatrix}}\end{bmatrix}}}
Αντικαθιστώντας τώρα τ たう ο おみくろん x σ しぐま τ たう η いーた ν にゅー τ たう η いーた ν にゅー
d
2
ψ ぷさい
d
x
2
=
−
8
π ぱい
2
m
h
2
[
E
−
V
(
x
)
]
ψ ぷさい ⇔
−
h
2
8
π ぱい
2
m
d
2
ψ ぷさい
d
x
2
+
V
(
x
)
ψ ぷさい =
E
ψ ぷさい
{\displaystyle {\frac {d^{2}\psi }{dx^{2}}}=-{\frac {8\pi ^{2}m}{h^{2}}}{\begin{bmatrix}E-V{\begin{pmatrix}x\end{pmatrix}}\end{bmatrix}}\psi \Leftrightarrow -{\frac {h^{2}}{8\pi ^{2}m}}{\frac {d^{2}\psi }{dx^{2}}}+V{\begin{pmatrix}x\end{pmatrix}}\psi =E\psi }
Επεκτείνοντας τώρα τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん μ みゅー ε いぷしろん κ かっぱ α あるふぁ ι いおた τ たう η いーた ν にゅー «εξίσωση Schrödinger» :
−
h
2
8
π ぱい
2
m
(
∂
2
ψ ぷさい
∂
x
2
+
∂
2
ψ ぷさい
∂
y
2
+
∂
2
ψ ぷさい
∂
z
2
)
+
V
(
x
,
y
,
z
)
ψ ぷさい =
E
ψ ぷさい
{\displaystyle -{\frac {h^{2}}{8\pi ^{2}m}}{\begin{pmatrix}{\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\end{pmatrix}}+V{\begin{pmatrix}x,y,z\end{pmatrix}}\psi =E\psi }
.
Η いーた μ みゅー ε いぷしろん τ たう η いーた δ でるた υ うぷしろん ο おみくろん
1. «Ανάδελτα τετράγωνο» :
∇
2
=
∂
2
ψ ぷさい
∂
x
2
+
∂
2
ψ ぷさい
∂
y
2
+
∂
2
ψ ぷさい
∂
z
2
{\displaystyle \nabla ^{2}={\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}}
−
h
2
8
π ぱい
2
m
∇
2
+
V
(
x
,
y
,
z
)
ψ ぷさい =
E
ψ ぷさい
{\displaystyle -{\frac {h^{2}}{8\pi ^{2}m}}\nabla ^{2}+V{\begin{pmatrix}x,y,z\end{pmatrix}}\psi =E\psi }
.
2. «Χάμιλτον» :
H
=
−
h
2
8
π ぱい
2
m
∇
2
+
V
(
x
,
y
,
z
)
{\displaystyle H=-{\frac {h^{2}}{8\pi ^{2}m}}\nabla ^{2}+V{\begin{pmatrix}x,y,z\end{pmatrix}}}
H
ψ ぷさい =
E
ψ ぷさい
{\displaystyle H\psi =E\psi }
.
Σύμφωνα μ みゅー ε いぷしろん τ たう η いーた ν にゅー « Αρχή της Αντιστοιχίας » τ たう ο おみくろん υ うぷしろん Bohr πρέπει ν にゅー α あるふぁ ν にゅー α あるふぁ ο おみくろん ι いおた κ かっぱ α あるふぁ ι いおた σ しぐま τ たう α あるふぁ Η いーた π ぱい ο おみくろん υ うぷしろん τ たう η いーた ν にゅー σ しぐま ε いぷしろん μ みゅー ε いぷしろん τ たう η いーた ν にゅー κ かっぱ α あるふぁ ι いおた τ たう ο おみくろん υ うぷしろん « συνάρτηση Hamilton » κ かっぱ α あるふぁ ι いおた τ たう ο おみくろん ν にゅー
H
f
=
1
2
m
(
p
x
2
+
p
y
2
+
p
z
2
)
+
V
(
x
,
y
,
z
)
{\displaystyle H_{f}={\frac {1}{2m}}{\begin{pmatrix}{p_{x}}^{2}+{p_{y}}^{2}+{p_{z}}^{2}\end{pmatrix}}+V{\begin{pmatrix}x,y,z\end{pmatrix}}}
όπου:
Hf : η いーた
m: η いーた τ たう ο おみくろん υ うぷしろん
px , py , pz : η いーた τ たう ο おみくろん υ うぷしろん τ たう ο おみくろん υ うぷしろん
V(x,y,z): η いーた τ たう ο おみくろん υ うぷしろん Είναι ολοφάνερη η いーた τ たう ο おみくろん υ うぷしろん κ かっぱ α あるふぁ ι いおた
p
x
→
−
i
h
2
π ぱい
∂
∂
x
⇔
p
x
2
→
−
h
2
4
π ぱい
2
∂
2
∂
x
2
{\displaystyle p_{x}\rightarrow -{\frac {ih}{2\pi }}{\frac {\partial }{\partial x}}\Leftrightarrow {p_{x}}^{2}\rightarrow -{\frac {h^{2}}{4\pi ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}}
Ομοίως βέβαια κ かっぱ α あるふぁ ι いおた γ がんま ι いおた α あるふぁ Επίσης, α あるふぁ ν にゅー
H
f
=
∑
i
=
1
n
[
1
2
m
i
(
p
x
i
2
+
p
y
i
2
+
p
z
i
2
)
+
V
(
x
i
,
y
i
,
z
i
)
]
{\displaystyle H_{f}=\sum _{i=1}^{n}{\begin{bmatrix}{\frac {1}{2m_{i}}}{\begin{pmatrix}{p_{x_{i}}}^{2}+{p_{y_{i}}}^{2}+{p_{z_{i}}}^{2}\end{pmatrix}}+V{\begin{pmatrix}x_{i},y_{i},z_{i}\end{pmatrix}}\end{bmatrix}}}
κ かっぱ α あるふぁ ι いおた
H
=
−
∑
i
=
1
n
[
h
2
8
π ぱい
2
m
i
(
∂
2
∂
x
i
2
+
∂
2
∂
y
i
2
+
∂
2
∂
z
i
2
)
+
V
(
x
i
,
y
i
,
z
i
)
]
{\displaystyle H=-\sum _{i=1}^{n}{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m_{i}}}{\begin{pmatrix}{\frac {\partial ^{2}}{\partial {x_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {y_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {z_{i}}^{2}}}\end{pmatrix}}+V{\begin{pmatrix}x_{i},y_{i},z_{i}\end{pmatrix}}\end{bmatrix}}}
Η いーた γ がんま ι いおた α あるふぁ
H
ψ ぷさい =
E
ψ ぷさい
{\displaystyle H\psi =E\psi }
Ο おみくろん ι いおた ψ ぷさい « ιδιοσυναρτήσεις » κ かっぱ α あるふぁ ι いおた ο おみくろん ι いおた Ε いぷしろん « ιδιοτιμές » .
Η いーた [ επεξεργασία ] Η いーた ψ ぷさい η いーた μ みゅー ι いおた α あるふぁ π ぱい ο おみくろん υ うぷしろん τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん τ たう ο おみくろん τ たう ω おめが ν にゅー τ たう ο おみくろん υ うぷしろん κ かっぱ α あるふぁ ι いおた μ みゅー ι いおた α あるふぁ Τ たう ο おみくろん τ たう η いーた σ しぐま τ たう ο おみくろん τ たう η いーた ν にゅー ν にゅー α あるふぁ τ たう ο おみくろん τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん σ しぐま ε いぷしろん τ たう ο おみくろん υ うぷしろん γ がんま ι いおた α あるふぁ τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん
∫
ψ ぷさい
2
d
V
=
1
{\displaystyle \int \psi ^{2}dV=1}
όπου:
V: ο おみくろん τ たう ο おみくろん υ うぷしろん Σ しぐま τ たう η いーた ν にゅー π ぱい ο おみくろん υ うぷしろん η いーた γ がんま ι いおた α あるふぁ μ みゅー ι いおた α あるふぁ ψ ぷさい η いーた « κανονικοποιημένη » .
Α あるふぁ ν にゅー γ がんま ι いおた α あるふぁ μ みゅー ι いおた α あるふぁ μ みゅー η いーた ν にゅー α あるふぁ τ たう η いーた ν にゅー τ たう η いーた ν にゅー μ みゅー ε いぷしろん « παράγοντα κανονικοποίησηης » (N), π ぱい ο おみくろん υ うぷしろん τ たう η いーた ν にゅー
N
−
2
=
∫
ψ ぷさい
2
d
V
⇔
N
=
1
(
∫
ψ ぷさい
2
d
V
)
2
{\displaystyle N^{-2}=\int \psi ^{2}dV\Leftrightarrow N={\frac {1}{{\begin{pmatrix}\int \psi ^{2}dV\end{pmatrix}}^{2}}}}
Έτσι προκύπτει μ みゅー ι いおた α あるふぁ ψ ぷさい 0 , γ がんま ι いおた α あるふぁ τ たう η いーた ν にゅー
ψ ぷさい
0
=
N
ψ ぷさい
{\displaystyle \psi _{0}=N\psi }
Τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん [ επεξεργασία ] Τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん υδρογόνου αποτελείται από ένα πρωτόνιο κ かっぱ α あるふぁ ι いおた π ぱい ο おみくろん υ うぷしろん κ かっぱ α あるふぁ ι いおた η いーた γ がんま ι いおた α あるふぁ τ たう ο おみくろん
H
ψ ぷさい =
E
ψ ぷさい
{\displaystyle H\psi =E\psi }
π ぱい ι いおた ο おみくろん
−
{
2
∑
i
=
1
[
h
2
8
π ぱい
2
m
i
∇
i
2
+
V
(
x
i
,
y
i
,
z
i
)
]
}
ψ ぷさい =
E
ψ ぷさい ⇔
−
[
h
2
8
π ぱい
2
m
p
∇
p
2
+
V
(
x
p
,
y
p
,
z
p
)
+
h
2
8
π ぱい
2
m
e
∇
e
2
+
V
(
x
e
,
y
e
,
z
e
)
]
ψ ぷさい =
E
ψ ぷさい
{\displaystyle -{\begin{Bmatrix}{\begin{matrix}2\\\sum \\i=1\end{matrix}}{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m_{i}}}{\nabla _{i}}^{2}+V{\begin{pmatrix}x_{i},y_{i},z_{i}\end{pmatrix}}\end{bmatrix}}\end{Bmatrix}}\psi =E\psi \Leftrightarrow -{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m_{p}}}{\nabla _{p}}^{2}+V{\begin{pmatrix}x_{p},y_{p},z_{p}\end{pmatrix}}+{\frac {h^{2}}{8\pi ^{2}m_{e}}}{\nabla _{e}}^{2}+V{\begin{pmatrix}x_{e},y_{e},z_{e}\end{pmatrix}}\end{bmatrix}}\psi =E\psi }
όπου
∇
i
2
=
∂
2
∂
x
i
2
+
∂
2
∂
y
i
2
+
∂
2
∂
z
i
2
{\displaystyle {\nabla _{i}}^{2}={\frac {\partial ^{2}}{\partial {x_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {y_{i}}^{2}}}+{\frac {\partial ^{2}}{\partial {z_{i}}^{2}}}}
όπου
xp , yp , zp : ο おみくろん ι いおた τ たう ο おみくろん υ うぷしろん σ しぐま τ たう ο おみくろん
xe , ye , ze : ο おみくろん ι いおた τ たう ο おみくろん υ うぷしろん σ しぐま τ たう ο おみくろん
mp : η いーた τ たう ο おみくろん υ うぷしろん
m
p
=
1
,
67262158
⋅
10
−
28
k
g
{\displaystyle m_{p}=1,67262158\cdot 10^{-28}\;kg}
me : η いーた τ たう ο おみくろん υ うぷしろん
m
e
=
9
,
1
⋅
10
−
31
k
g
{\displaystyle m_{e}=9,1\cdot 10^{-31}\;kg}
Σ しぐま τ たう η いーた ν にゅー π ぱい ο おみくろん υ うぷしろん « ισότοπο » τ たう ο おみくろん υ うぷしろん 1 Η いーた τ たう ο おみくろん « δευτέριο »΄ ) ή τ たう ο おみくろん « τρίτιο »΄ ), έχουμε αντίστοιχα md ή mt αντί mp . Σ しぐま τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん Γ がんま ι いおた τ たう α あるふぁ σ しぐま τ たう η いーた ν にゅー « κινητική » τ たう ω おめが ν にゅー Επειδή όμως τ たう ο おみくろん σ しぐま ε いぷしろん τ たう ο おみくろん η いーた τ たう ο おみくろん υ うぷしろん π ぱい ο おみくろん υ うぷしろん τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん σ しぐま ε いぷしろん μ みゅー ε いぷしろん τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん γ がんま ι いおた α あるふぁ ν にゅー α あるふぁ σ しぐま τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん τ たう ω おめが ν にゅー Μ みゅー ε いぷしろん τ たう η いーた ν にゅー ψ ぷさい τ たう η いーた ν にゅー τ たう ο おみくろん υ うぷしろん κ かっぱ α あるふぁ ι いおた τ たう α あるふぁ π ぱい ο おみくろん υ うぷしろん « ατομικά τροχιακά υδρογόνου » . Σ しぐま τ たう η いーた ν にゅー κ かっぱ α あるふぁ ι いおた π ぱい ι いおた α あるふぁ
H
ψ ぷさい =
E
ψ ぷさい
{\displaystyle H\psi =E\psi }
π ぱい ι いおた ο おみくろん
−
[
h
2
8
π ぱい
2
m
∇
2
+
q
2
4
π ぱい
ϵ
0
1
x
2
+
y
2
+
z
2
]
ψ ぷさい =
E
ψ ぷさい
{\displaystyle -{\begin{bmatrix}{\frac {h^{2}}{8\pi ^{2}m}}\nabla ^{2}+{\frac {q^{2}}{4\pi \epsilon _{0}}}{\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{bmatrix}}\psi =E\psi }
όπου
q: Τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん
q
=
1
,
60210
⋅
10
−
19
C
b
{\displaystyle q=1,60210\cdot 10^{-19}\;Cb}
ε いぷしろん 0 : « Διηλεκτρική σταθερά τ たう ο おみくろん υ うぷしろん :
ϵ
0
≃
8
,
85418
⋅
10
−
12
C
b
2
/
N
t
m
2
{\displaystyle \epsilon _{0}\simeq 8,85418\cdot 10^{-12}\;Cb^{2}/Ntm^{2}}
Διαπιστώνουμε σ しぐま τ たう η いーた ν にゅー ο おみくろん ι いおた σ しぐま τ たう η いーた τ たう ο おみくろん υ うぷしろん τ たう ο おみくろん υ うぷしろん
V
(
x
,
y
,
z
)
=
q
2
4
π ぱい
ϵ
0
1
x
2
+
y
2
+
z
2
{\displaystyle V{\begin{pmatrix}x,y,z\end{pmatrix}}={\frac {q^{2}}{4\pi \epsilon _{0}}}{\frac {1}{\sqrt {x^{2}+y^{2}+z^{2}}}}}
ν にゅー α あるふぁ σ しぐま ε いぷしろん « σφαιρικές συντεταγμένες » , μ みゅー ε いぷしろん π ぱい ο おみくろん υ うぷしろん τ たう η いーた ν にゅー « τριγωνομετρία » :
x
=
r
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle x=r\eta \mu \theta \sigma \upsilon \nu \phi }
y
=
r
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle y=r\eta \mu \theta \eta \mu \phi }
z
=
r
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle z=r\sigma \upsilon \nu \theta }
Τετραγωνίζοντας τις παραπάνω σχέσεις κατά μέλη κ かっぱ α あるふぁ ι いおた σ しぐま τ たう η いーた ν にゅー π ぱい ο おみくろん υ うぷしろん
r
2
=
x
2
+
y
2
+
z
2
⇔
r
=
x
2
+
y
2
+
z
2
{\displaystyle r^{2}=x^{2}+y^{2}+z^{2}\Leftrightarrow r={\sqrt {x^{2}+y^{2}+z^{2}}}}
Μ みゅー ε いぷしろん σ しぐま ε いぷしろん ο おみくろん τ たう ο おみくろん υ うぷしろん σ しぐま τ たう η いーた ν にゅー γ がんま ι いおた α あるふぁ τ たう ο おみくろん κ かっぱ α あるふぁ ι いおた
V
=
−
q
2
4
π ぱい
ϵ
0
1
r
{\displaystyle V=-{\frac {q^{2}}{4\pi \epsilon _{0}}}{\frac {1}{r}}}
ο おみくろん κ かっぱ α あるふぁ ι いおた
∇
2
=
1
r
2
[
∂
∂
r
(
r
2
∂
∂
r
)
+
1
η いーた
μ みゅー
2
θ しーた
∂
2
∂
ϕ
2
+
1
η いーた μ みゅー θ しーた
∂
∂
θ しーた
(
η いーた μ みゅー θ しーた
∂
∂
θ しーた
)
]
{\displaystyle \nabla ^{2}={\frac {1}{r^{2}}}{\begin{bmatrix}{\frac {\partial }{\partial r}}{\begin{pmatrix}r^{2}{\frac {\partial }{\partial r}}\end{pmatrix}}+{\frac {1}{\eta \mu ^{2}\theta }}{\frac {\partial ^{2}}{\partial \phi ^{2}}}+{\frac {1}{\eta \mu \theta }}{\frac {\partial }{\partial \theta }}{\begin{pmatrix}\eta \mu \theta {\frac {\partial }{\partial \theta }}\end{pmatrix}}\end{bmatrix}}}
Μ みゅー ε いぷしろん τ たう α あるふぁ η いーた γ がんま ι いおた α あるふぁ τ たう ο おみくろん σ しぐま ε いぷしろん
−
h
2
8
π ぱい
2
m
r
2
[
∂
∂
r
(
r
2
∂
ψ ぷさい
∂
r
)
+
1
η いーた
μ みゅー
2
θ しーた
∂
2
ψ ぷさい
∂
ϕ
2
+
1
η いーた μ みゅー θ しーた
∂
∂
θ しーた
(
η いーた μ みゅー θ しーた
∂
ψ ぷさい
∂
θ しーた
)
]
−
q
2
4
π ぱい
ϵ
0
r
ψ ぷさい =
E
ψ ぷさい ⇔
∂
∂
r
(
r
2
∂
ψ ぷさい
∂
r
)
+
1
η いーた
μ みゅー
2
θ しーた
∂
2
ψ ぷさい
∂
ϕ
2
+
1
η いーた μ みゅー θ しーた
∂
∂
θ しーた
(
η いーた μ みゅー θ しーた
∂
ψ ぷさい
∂
θ しーた
)
+
2
π ぱい m
q
2
r
h
2
ϵ
0
ψ ぷさい =
−
8
π ぱい
2
m
r
2
h
2
E
ψ ぷさい
{\displaystyle -{\frac {h^{2}}{8\pi ^{2}mr^{2}}}{\begin{bmatrix}{\frac {\partial }{\partial r}}{\begin{pmatrix}r^{2}{\frac {\partial \psi }{\partial r}}\end{pmatrix}}+{\frac {1}{\eta \mu ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}+{\frac {1}{\eta \mu \theta }}{\frac {\partial }{\partial \theta }}{\begin{pmatrix}\eta \mu \theta {\frac {\partial \psi }{\partial \theta }}\end{pmatrix}}\end{bmatrix}}-{\frac {q^{2}}{4\pi \epsilon _{0}r}}\psi =E\psi \Leftrightarrow {\frac {\partial }{\partial r}}{\begin{pmatrix}r^{2}{\frac {\partial \psi }{\partial r}}\end{pmatrix}}+{\frac {1}{\eta \mu ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}+{\frac {1}{\eta \mu \theta }}{\frac {\partial }{\partial \theta }}{\begin{pmatrix}\eta \mu \theta {\frac {\partial \psi }{\partial \theta }}\end{pmatrix}}+{\frac {2\pi mq^{2}r}{h^{2}\epsilon _{0}}}\psi =-{\frac {8\pi ^{2}mr^{2}}{h^{2}}}E\psi }
Παρά τ たう ο おみくろん η いーた σ しぐま τ たう η いーた ν にゅー η いーた γ がんま ι いおた α あるふぁ ψ ぷさい θ しーた φ ふぁい
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
R
(
r
)
Y
(
θ しーた ,
ϕ
)
=
R
(
r
)
Θ しーた
(
θ しーた
)
Φ ふぁい
(
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}=R{\begin{pmatrix}r\end{pmatrix}}Y{\begin{pmatrix}\theta ,\phi \end{pmatrix}}=R{\begin{pmatrix}r\end{pmatrix}}\Theta {\begin{pmatrix}\theta \end{pmatrix}}\Phi {\begin{pmatrix}\phi \end{pmatrix}}}
Τ たう α あるふぁ « ατομικά τροχιακά » π ぱい ο おみくろん υ うぷしろん « κβαντικούς αριθμούς » , n,
ℓ
{\displaystyle \ell }
κ かっぱ α あるふぁ ι いおた s :
Ο おみくろん « κύριος κβαντικός αριθμός » n, παίρνει τιμές: 1, 2, 3,... 7. Θεωρητικά προβλέπονται κ かっぱ α あるふぁ ι いおた η いーた π ぱい ο おみくろん υ うぷしろん σ しぐま τ たう α あるふぁ Ο おみくろん
ℓ
{\displaystyle \ell }
Ο おみくろん
ℓ
{\displaystyle \ell }
O κβαντικός αριθμός ms (σ しぐま π ぱい ι いおた ν にゅー Ο おみくろん ι いおた τ たう ω おめが ν にゅー
1s: n=1,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
π ぱい
e
−
ρ ろー
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{\sqrt {\pi }}}e^{-\rho }}
ρ ろー =
r
α あるふぁ
0
{\displaystyle \rho ={\frac {r}{\alpha _{0}}}}
μ みゅー ε いぷしろん
α あるふぁ
0
=
h
2
ϵ
0
π ぱい
m
e
q
e
2
{\displaystyle \alpha _{0}={\frac {h^{2}\epsilon _{0}}{\pi m_{e}{q_{e}}^{2}}}}
« ακτίνα Bohr » . 1s1 , δηλαδή τ たう ο おみくろん σ しぐま τ たう ο おみくろん η いーた γ がんま ι いおた α あるふぁ τ たう ο おみくろん τ たう ο おみくろん υ うぷしろん Ο おみくろん ι いおた τ たう η いーた ν にゅー τ たう η いーた ν にゅー θ しーた α あるふぁ σ しぐま ε いぷしろん μ みゅー ε いぷしろん
v
=
Δ でるた E
/
h
{\displaystyle v=\Delta E/h}
2s: n=2,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
4
2
π ぱい
(
2
−
ρ ろー
)
e
−
ρ ろー 2
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}{\begin{pmatrix}2-\rho \end{pmatrix}}e^{-{\frac {\rho }{2}}}}
2px : n=2,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
4
2
π ぱい
r
e
−
ρ ろー 2
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}re^{-{\frac {\rho }{2}}}\eta \mu \theta \sigma \upsilon \nu \phi }
2py : n=2,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
4
2
π ぱい
r
e
−
ρ ろー 2
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}re^{-{\frac {\rho }{2}}}\eta \mu \theta \eta \mu \phi }
2pz : n=2,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
4
2
π ぱい
r
e
−
ρ ろー 2
σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{4{\sqrt {2\pi }}}}re^{-{\frac {\rho }{2}}}\sigma \upsilon \nu \phi }
3s: n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
81
3
π ぱい
(
27
−
18
ρ ろー +
2
ρ ろー
2
)
e
−
ρ ろー 3
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{81{\sqrt {3\pi }}}}{\begin{pmatrix}27-18\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{3}}}}
3px : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
81
2
π ぱい
r
(
6
−
ρ ろー
)
e
−
ρ ろー 3
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2}{81{\sqrt {2\pi }}}}r{\begin{pmatrix}6-\rho \end{pmatrix}}e^{-{\frac {\rho }{3}}}\eta \mu \theta \sigma \upsilon \nu \phi }
3py : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
81
2
π ぱい
r
(
6
−
ρ ろー
)
e
−
ρ ろー 3
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2}{81{\sqrt {2\pi }}}}r{\begin{pmatrix}6-\rho \end{pmatrix}}e^{-{\frac {\rho }{3}}}\eta \mu \theta \eta \mu \phi }
3pz : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
81
2
π ぱい
r
(
6
−
ρ ろー
)
e
−
ρ ろー 3
σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2}{81{\sqrt {2\pi }}}}r{\begin{pmatrix}6-\rho \end{pmatrix}}e^{-{\frac {\rho }{3}}}\sigma \upsilon \nu \phi }
3dz2 : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
81
6
π ぱい
r
2
e
−
ρ ろー 3
(
3
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
1
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{81{\sqrt {6\pi }}}}r^{2}e^{-{\frac {\rho }{3}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}}
3dzx : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
81
π ぱい
r
2
e
−
ρ ろー 3
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {2}}{81{\sqrt {\pi }}}}r^{2}e^{-{\frac {\rho }{3}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi }
3dyz : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
81
π ぱい
r
2
e
−
ρ ろー 3
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {2}}{81{\sqrt {\pi }}}}r^{2}e^{-{\frac {\rho }{3}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi }
3dx2 -y2 : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
81
2
π ぱい
ρ ろー
2
e
−
ρ ろー 3
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー
(
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{81{\sqrt {2\pi }}}}\rho ^{2}e^{-{\frac {\rho }{3}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}}
3dxy : n=3,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
81
π ぱい
ρ ろー
2
e
−
ρ ろー 3
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {2}}{81{\sqrt {\pi }}}}\rho ^{2}e^{-{\frac {\rho }{3}}}\eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
4s: n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
1536
π ぱい
(
192
−
144
ρ ろー +
24
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 4
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{1536{\sqrt {\pi }}}}{\begin{pmatrix}192-144\rho +24\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{4}}}}
4px : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
256
5
π ぱい
r
(
80
−
20
ρ ろー −
ρ ろー
2
)
e
−
ρ ろー 4
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{256{\sqrt {5\pi }}}}r{\begin{pmatrix}80-20\rho -\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \sigma \upsilon \nu \phi }
4py : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
256
5
π ぱい
r
(
80
−
20
ρ ろー −
ρ ろー
2
)
e
−
ρ ろー 4
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{256{\sqrt {5\pi }}}}r{\begin{pmatrix}80-20\rho -\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \eta \mu \phi }
4pz : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
256
5
π ぱい
r
(
80
−
20
ρ ろー −
ρ ろー
2
)
e
−
ρ ろー 4
σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{256{\sqrt {5\pi }}}}r{\begin{pmatrix}80-20\rho -\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{4}}}\sigma \upsilon \nu \phi }
4dz2 : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
3.072
π ぱい
r
2
(
12
−
ρ ろー
)
e
−
ρ ろー 4
(
3
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
1
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}}
4dzx : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
1.536
π ぱい
r
2
(
12
−
ρ ろー
)
e
−
ρ ろー 4
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi }
4dyz : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
1.536
π ぱい
r
2
(
12
−
ρ ろー
)
e
−
ρ ろー 4
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi }
4dx2 -y2 : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
1.536
π ぱい
r
2
(
12
−
ρ ろー
)
e
−
ρ ろー 4
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー
(
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}}
4dxy : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
1.536
π ぱい
r
2
(
12
−
ρ ろー
)
e
−
ρ ろー 4
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1.536{\sqrt {\pi }}}}r^{2}{\begin{pmatrix}12-\rho \end{pmatrix}}e^{-{\frac {\rho }{4}}}\eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
4fx3 : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
3.072
5
π ぱい
r
3
e
−
ρ ろー 4
(
5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {5\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
4fy3 : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
3.072
5
π ぱい
r
3
e
−
ρ ろー 4
(
5
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {5\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi }
4fz3 : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
3.072
5
π ぱい
r
3
e
−
ρ ろー 4
(
5
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
)
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{3.072{\sqrt {5\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta }
4fx(z2 -y2 ) : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
3.072
π ぱい
r
3
e
−
ρ ろー 4
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{3.072{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
4fy(z2 -x2 ) : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
3.072
π ぱい
r
3
e
−
ρ ろー 4
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{3.072{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi }
4fz(x2 -y2 ) : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
3.072
π ぱい
r
3
e
−
ρ ろー 4
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{3.072{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta }
4fxyz : n=4,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
1536
π ぱい
r
3
e
−
ρ ろー 4
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{1536{\sqrt {\pi }}}}r^{3}e^{-{\frac {\rho }{4}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
5s: n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
5
π ぱい
(
18.750
−
15.000
ρ ろー +
3.000
ρ ろー
2
−
200
ρ ろー
3
+
4
ρ ろー
4
)
e
−
ρ ろー 5
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {5\pi }}}}{\begin{pmatrix}18.750-15.000\rho +3.000\rho ^{2}-200\rho ^{3}+4\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{5}}}}
5px : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
10
π ぱい
r
(
7.500
−
2.250
ρ ろー +
180
ρ ろー
2
−
4
ρ ろー
3
)
e
−
ρ ろー 5
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r{\begin{pmatrix}7.500-2.250\rho +180\rho ^{2}-4\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \sigma \upsilon \nu \phi }
5py : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
10
π ぱい
r
(
7.500
−
2.250
ρ ろー +
180
ρ ろー
2
−
4
ρ ろー
3
)
e
−
ρ ろー 5
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r{\begin{pmatrix}7.500-2.250\rho +180\rho ^{2}-4\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \eta \mu \phi }
5pz : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
10
π ぱい
r
(
7.500
−
2.250
ρ ろー +
180
ρ ろー
2
−
4
ρ ろー
3
)
e
−
ρ ろー 5
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r{\begin{pmatrix}7.500-2.250\rho +180\rho ^{2}-4\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\sigma \upsilon \nu \theta }
5dz2 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
35
π ぱい
r
2
(
525
−
70
ρ ろー +
2
ρ ろー
2
)
e
−
ρ ろー 5
(
3
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
1
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}}
5dzx : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
3
46.875
14
π ぱい
r
2
(
525
−
70
ρ ろー +
2
ρ ろー
2
)
e
−
ρ ろー 5
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46.875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi }
5dyz : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
3
46.875
14
π ぱい
r
2
(
525
−
70
ρ ろー +
2
ρ ろー
2
)
e
−
ρ ろー 5
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46.875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi }
5dx2 -y2 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
46875
14
π ぱい
r
2
(
525
−
70
ρ ろー +
2
ρ ろー
2
)
e
−
ρ ろー 5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー
(
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}}
5dxy : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
3
46.875
14
π ぱい
r
2
(
525
−
70
ρ ろー +
2
ρ ろー
2
)
e
−
ρ ろー 5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46.875{\sqrt {14\pi }}}}r^{2}{\begin{pmatrix}525-70\rho +2\rho ^{2}\end{pmatrix}}e^{-{\frac {\rho }{5}}}\eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
5fx3 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
10
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
(
5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
5fy3 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
10
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
(
5
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi }
5fz3 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
46.875
10
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
(
5
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
)
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{46.875{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta }
5fx(z2 -y2 ) : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
46.875
2
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46.875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
5fy(z2 -x2 ) : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
46.875
2
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46.875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi }
5fz(x2 -y2 ) : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
46.875
2
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{46.875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta }
5fxyz : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
2
3
46875
2
π ぱい
r
3
(
20
−
ρ ろー
)
e
−
ρ ろー 5
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {2{\sqrt {3}}}{46875{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}20-\rho \end{pmatrix}}e^{-{\frac {\rho }{5}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
5gz4 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
(
35
σ しぐま υ うぷしろん
ν にゅー
4
θ しーた −
30
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた +
3
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}35\sigma \upsilon \nu ^{4}\theta -30\sigma \upsilon \nu ^{2}\theta +3\end{pmatrix}}}
5gz2 x : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
(
4
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta }
5gz2 y : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
(
4
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi \sigma \upsilon \nu \theta }
5gz2 xy : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
(
6
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた
μ みゅー
2
θ しーた η いーた μ みゅー ϕ
σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta \eta \mu \phi \sigma \upsilon \nu \phi }
5gz2 (x2 -y2 ) : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
(
6
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
η いーた
μ みゅー
2
θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta }
5gzx3 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
η いーた
μ みゅー
3
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
(
1
−
4
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-4\eta \mu ^{2}\phi \end{pmatrix}}}
5gzy3 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
η いーた
μ みゅー
3
θ しーた η いーた μ みゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
(
3
−
4
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{3}\theta \eta \mu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}3-4\eta \mu ^{2}\phi \end{pmatrix}}}
5gxy(x2 -y2 ) : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
η いーた
μ みゅー
3
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}}
5gx4 +y4 : n=5,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
28.800
70
π ぱい
r
4
e
−
ρ ろー 5
η いーた
μ みゅー
4
θ しーた
(
1
−
4
σ しぐま υ うぷしろん
ν にゅー
2
ϕ
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{28.800{\sqrt {70\pi }}}}r^{4}e^{-{\frac {\rho }{5}}}\eta \mu ^{4}\theta {\begin{pmatrix}1-4\sigma \upsilon \nu ^{2}\phi \eta \mu ^{2}\phi \end{pmatrix}}}
6s: n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
1.049.760
6
π ぱい
(
174.960
−
145.800
ρ ろー +
32.400
ρ ろー
2
−
2.700
ρ ろー
3
+
90
ρ ろー
4
−
ρ ろー
5
)
e
−
ρ ろー 6
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{1.049.760{\sqrt {6\pi }}}}{\begin{pmatrix}174.960-145.800\rho +32.400\rho ^{2}-2.700\rho ^{3}+90\rho ^{4}-\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{6}}}}
6px : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
12.186
70
π ぱい
r
(
5.506.240
−
1.870.830
ρ ろー +
183.708
ρ ろー
2
−
6.804
ρ ろー
3
+
81
ρ ろー
4
)
e
−
ρ ろー 6
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{12.186{\sqrt {70\pi }}}}r{\begin{pmatrix}5.506.240-1.870.830\rho +183.708\rho ^{2}-6.804\rho ^{3}+81\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \sigma \upsilon \nu \phi }
6py : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
12.186
70
π ぱい
r
(
5.506.240
−
1.870.830
ρ ろー +
183.708
ρ ろー
2
−
6.804
ρ ろー
3
+
81
ρ ろー
4
)
e
−
ρ ろー 6
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{12.186{\sqrt {70\pi }}}}r{\begin{pmatrix}5.506.240-1.870.830\rho +183.708\rho ^{2}-6.804\rho ^{3}+81\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \eta \mu \phi }
6pz : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
12.186
70
π ぱい
r
(
5.506.240
−
1.870.830
ρ ろー +
183.708
ρ ろー
2
−
6.804
ρ ろー
3
+
81
ρ ろー
4
)
e
−
ρ ろー 6
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{12.186{\sqrt {70\pi }}}}r{\begin{pmatrix}5.506.240-1.870.830\rho +183.708\rho ^{2}-6.804\rho ^{3}+81\rho ^{4}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\sigma \upsilon \nu \theta }
6dz2 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
839.808
21
π ぱい
r
2
(
9.072
−
1.512
ρ ろー +
72
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 6
(
3
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
1
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{839.808{\sqrt {21\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}}
6dzx : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
419.904
35
π ぱい
r
2
(
9.072
−
1.512
ρ ろー +
72
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 6
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{419.904{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi }
6dyz : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
419.904
35
π ぱい
r
2
(
9.072
−
1.512
ρ ろー +
72
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 6
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{419.904{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi }
6dx2 -y2 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
839.808
35
π ぱい
r
2
(
9.072
−
1.512
ρ ろー +
72
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 6
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー
(
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{839.808{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}}
6dxy : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
419.904
35
π ぱい
r
2
(
9.072
−
1.512
ρ ろー +
72
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 6
(
5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{419.904{\sqrt {35\pi }}}}r^{2}{\begin{pmatrix}9.072-1.512\rho +72\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
6fx3 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
97.200
10
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{97.200{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
6fy3 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
97.200
10
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
5
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{97.200{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi }
6fz3 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
97.200
10
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
5
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
)
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{97.200{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta }
6fx(z2 -y2 ) : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
97.200
2
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{97.200{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
6fy(z2 -x2 ) : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
97.200
2
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{97.200{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi }
6fz(x2 -y2 ) : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
97.200
2
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{97.200{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta }
6fxyz : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
194.400
2
π ぱい
r
3
(
24
−
ρ ろー
)
e
−
ρ ろー 6
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{194.400{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
6gz4 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
35
σ しぐま υ うぷしろん
ν にゅー
4
θ しーた −
30
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた +
3
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}35\sigma \upsilon \nu ^{4}\theta -30\sigma \upsilon \nu ^{2}\theta +3\end{pmatrix}}}
6gz2 x : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
4
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta }
6gz2 y : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
4
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}4\sigma \upsilon \nu ^{2}\theta -3\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi \sigma \upsilon \nu \theta }
6gz2 xy : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
6
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた
μ みゅー
2
θ しーた η いーた μ みゅー ϕ
σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta \eta \mu \phi \sigma \upsilon \nu \phi }
6gz2 (x2 -y2 ) : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
(
6
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
η いーた
μ みゅー
2
θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}{\begin{pmatrix}6\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\eta \mu ^{2}\theta }
6gzx3 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
η いーた
μ みゅー
3
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
(
1
−
4
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-4\eta \mu ^{2}\phi \end{pmatrix}}}
6gzy3 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
η いーた
μ みゅー
3
θ しーた η いーた μ みゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
(
3
−
4
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{3}\theta \eta \mu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}3-4\eta \mu ^{2}\phi \end{pmatrix}}}
6gxy(x2 -y2 ) : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
η いーた
μ みゅー
3
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
σ しぐま υ うぷしろん ν にゅー θ しーた
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{3}\theta \sigma \upsilon \nu \phi \sigma \upsilon \nu \theta {\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}}
6gx4 +y4 : n=6,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
k
457.400
70
π ぱい
r
4
(
24
−
ρ ろー
)
e
−
ρ ろー 6
η いーた
μ みゅー
4
θ しーた
(
1
−
4
σ しぐま υ うぷしろん
ν にゅー
2
ϕ
η いーた
μ みゅー
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {k}{457.400{\sqrt {70\pi }}}}r^{4}{\begin{pmatrix}24-\rho \end{pmatrix}}e^{-{\frac {\rho }{6}}}\eta \mu ^{4}\theta {\begin{pmatrix}1-4\sigma \upsilon \nu ^{2}\phi \eta \mu ^{2}\phi \end{pmatrix}}}
7s: n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
117.649
k
π ぱい
(
296.475.480
−
254.121.408
ρ ろー +
60.505.200
ρ ろー
2
−
5.762.400
ρ ろー
3
+
246.960
ρ ろー
4
−
4.704
ρ ろー
5
+
32
ρ ろー
6
)
e
−
ρ ろー 7
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{117.649k{\sqrt {\pi }}}}{\begin{pmatrix}296.475.480-254.121.408\rho +60.505.200\rho ^{2}-5.762.400\rho ^{3}+246.960\rho ^{4}-4.704\rho ^{5}+32\rho ^{6}\end{pmatrix}}e^{-{\frac {\rho }{7}}}}
7px : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
117.649
k
π ぱい
r
(
112.943.040
−
40.336.800
ρ ろー +
4.609.920
ρ ろー
2
−
164.640
ρ ろー
3
+
4.480
ρ ろー
4
−
32
ρ ろー
5
)
e
−
ρ ろー 7
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{117.649k{\sqrt {\pi }}}}r{\begin{pmatrix}112.943.040-40.336.800\rho +4.609.920\rho ^{2}-164.640\rho ^{3}+4.480\rho ^{4}-32\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \sigma \upsilon \nu \phi }
7py : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
117.649
k
π ぱい
r
(
112.943.040
−
40.336.800
ρ ろー +
4.609.920
ρ ろー
2
−
164.640
ρ ろー
3
+
4.480
ρ ろー
4
−
32
ρ ろー
5
)
e
−
ρ ろー 7
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{117.649k{\sqrt {\pi }}}}r{\begin{pmatrix}112.943.040-40.336.800\rho +4.609.920\rho ^{2}-164.640\rho ^{3}+4.480\rho ^{4}-32\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \eta \mu \phi }
7pz : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
117.649
k
π ぱい
r
(
112.943.040
−
40.336.800
ρ ろー +
4.609.920
ρ ろー
2
−
164.640
ρ ろー
3
+
4.480
ρ ろー
4
−
32
ρ ろー
5
)
e
−
ρ ろー 7
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{117.649k{\sqrt {\pi }}}}r{\begin{pmatrix}112.943.040-40.336.800\rho +4.609.920\rho ^{2}-164.640\rho ^{3}+4.480\rho ^{4}-32\rho ^{5}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\sigma \upsilon \nu \theta }
7dz2 : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
453.789
21
π ぱい
r
2
(
14.406
−
2.958
ρ ろー +
84
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 7
(
3
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
1
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {21\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}3\sigma \upsilon \nu ^{2}\theta -1\end{pmatrix}}}
7dzx : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
453.789
7
π ぱい
r
2
(
14.406
−
2.958
ρ ろー +
84
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 7
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \sigma \upsilon \nu \theta \sigma \upsilon \nu \phi }
7dyz : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
453.789
7
π ぱい
r
2
(
14.406
−
2.958
ρ ろー +
84
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 7
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu \theta \sigma \upsilon \nu \theta \eta \mu \phi }
7dx2 -y2 : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
907.578
7
π ぱい
r
2
(
14.406
−
2.958
ρ ろー +
84
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 7
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー
(
2
ϕ
)
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{907.578{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}\eta \mu ^{2}\theta \sigma \upsilon \nu {\begin{pmatrix}2\phi \end{pmatrix}}}
7dxy : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
453.789
7
π ぱい
r
2
(
14.406
−
2.958
ρ ろー +
84
ρ ろー
2
−
ρ ろー
3
)
e
−
ρ ろー 7
(
5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{453.789{\sqrt {7\pi }}}}r^{2}{\begin{pmatrix}14.406-2.958\rho +84\rho ^{2}-\rho ^{3}\end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
7fx3 : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
180.075
10
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
(
5
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{180.075{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
7fy3 : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
180.075
10
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
(
5
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
−
3
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{180.075{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\eta \mu ^{2}\theta \eta \mu ^{2}\phi -3\end{pmatrix}}\eta \mu \theta \eta \mu \phi }
7fz3 : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
1
180.075
10
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
(
5
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
3
)
σ しぐま υ うぷしろん ν にゅー θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {1}{180.075{\sqrt {10\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}5\sigma \upsilon \nu ^{2}\theta -3\end{pmatrix}}\sigma \upsilon \nu \theta }
7fx(z2 -y2 ) : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
180.075
2
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた η いーた
μ みゅー
2
ϕ
)
η いーた μ みゅー θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{180.075{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \eta \mu ^{2}\phi \end{pmatrix}}\eta \mu \theta \sigma \upsilon \nu \phi }
7fy(z2 -x2 ) : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
180.075
2
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
(
σ しぐま υ うぷしろん
ν にゅー
2
θ しーた −
η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん
ν にゅー
2
ϕ
)
η いーた μ みゅー θ しーた η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{180.075{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}\sigma \upsilon \nu ^{2}\theta -\eta \mu ^{2}\theta \sigma \upsilon \nu ^{2}\phi \end{pmatrix}}\eta \mu \theta \eta \mu \phi }
7fz(x2 -y2 ) : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
180.075
2
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
(
1
−
2
η いーた
μ みゅー
2
ϕ
)
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{180.075{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}{\begin{pmatrix}1-2\eta \mu ^{2}\phi \end{pmatrix}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta }
7fxyz : n=7,
ℓ
{\displaystyle \ell }
ψ ぷさい
(
r
,
θ しーた ,
ϕ
)
=
3
360.150
2
π ぱい
r
3
(
28
−
ρ ろー
)
e
−
ρ ろー 7
σ しぐま υ うぷしろん ν にゅー θ しーた η いーた
μ みゅー
2
θ しーた σ しぐま υ うぷしろん ν にゅー ϕ
η いーた μ みゅー ϕ
{\displaystyle \psi {\begin{pmatrix}r,\theta ,\phi \end{pmatrix}}={\frac {\sqrt {3}}{360.150{\sqrt {2\pi }}}}r^{3}{\begin{pmatrix}28-\rho \end{pmatrix}}e^{-{\frac {\rho }{7}}}\sigma \upsilon \nu \theta \eta \mu ^{2}\theta \sigma \upsilon \nu \phi \eta \mu \phi }
Τ たう ο おみくろん τ たう ω おめが ν にゅー [ επεξεργασία ] Περιοδικός πίνακας Medeleev [ επεξεργασία ] Σύγχρονος Περιοδικός Πίνακας [ επεξεργασία ] Περιοδικές ιδιότητες τ たう ω おめが ν にゅー [ επεξεργασία ] Ανωμαλίες τ たう ο おみくろん υ うぷしろん [ επεξεργασία ] Ο おみくろん [ επεξεργασία ]