Graph of a function

In mathematics, the graph of a function $f$ is defined as the set of ordered pairs $(x, y)$ , where $f (x) = y$ . In the common case where $x$ and $f (x)$ are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane.

In the case of functions of two variables, that is functions whose domain consists of pairs $(x, y)$ , the graph usually refers to the set of ordered triples $(x, y, z)$ where $f (x, y) = z$ , instead of the pairs $((x, y), z)$ as in the definition above. This set is a subset of three-dimensional space; for a continuous real-valued function of two real variables, it is a surface.

A graph of a function is a special case of a relation.

In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see Plot (graphics) for details.

In the modern foundations of mathematics, and, typically, in set theory, a function is actually equal to its graph.^[1] However, it is often useful to see functions as mappings,^[2] which consist not only of the relation between input and output, but also which set is the domain, and which set is the codomain. For example, to say that a function is onto (surjective) or not the codomain should be taken into account. The graph of a function on its own doesn't determine the codomain. It is common^[3] to use both terms function and graph of a function since even if considered the same object, they indicate viewing it from a different perspective.

Definition

Given a mapping $f:X\to Y$ , in other words a function $f$ together with its domain $X$ and codomain $Y$ , the graph of the mapping is^[4] the set

G(f)=\{(x,f(x))\mid x\in X\}

,

which is a subset of $X\times Y$ . In the abstract definition of a function, $G(f)$ is actually equal to $f$ .

One can observe that, if, $f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ , then the graph $G(f)$ is a subset of $\mathbb {R} ^{n+m}$ (strictly speaking it is $\mathbb {R} ^{n}\times \mathbb {R} ^{m}$ , but one can embed it with the natural isomorphism).

Examples

Functions of one variable

Graph of the function f(x, y) = sin(x²) · cos(y²).

The graph of the function $f:\{1,2,3\}\to \{a,b,c,d\}$ defined by

f(x)={\begin{cases}a,&{\text{if }}x=1,\\d,&{\text{if }}x=2,\\c,&{\text{if }}x=3,\end{cases}}

is the subset of the set $\{1,2,3\}\times \{a,b,c,d\}$

G(f)=\{(1,a),(2,d),(3,c)\}.\,

From the graph, the domain $\{1,2,3\}$ is recovered as the set of first component of each pair in the graph $\{1,2,3\}=\{x:\ {\text{there exists }}y,{\text{ such that }}(x,y)\in G(f)\}$ . Similarly, the range can be recovered as $\{a,c,d\}=\{y:{\text{there exists }}x,{\text{ such that }}(x,y)\in G(f)\}$ . The codomain $\{a,b,c,d\}$ , however, cannot be determined from the graph alone.

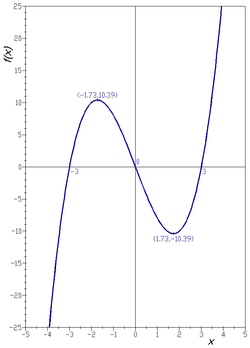
The graph of the cubic polynomial on the real line

f(x)=x^{3}-9x\,

is

\{(x,x^{3}-9x):x{\text{ is a real number}}\}.\,

If this set is plotted on a Cartesian plane, the result is a curve (see figure).

Functions of two variables

Plot of the graph of f(x, y) = −(cos(x²) + cos(y²))², also showing its gradient projected on the bottom plane.

The graph of the trigonometric function

f(x,y)=\sin(x^{2})\cos(y^{2})\,

is

\{(x,y,\sin(x^{2})\cos(y^{2})):x{\text{ and }}y{\text{ are real numbers}}\}.

If this set is plotted on a three dimensional Cartesian coordinate system, the result is a surface (see figure).

Oftentimes it is helpful to show with the graph, the gradient of the function and several level curves. The level curves can be mapped on the function surface or can be projected on the bottom plane. The second figure shows such a drawing of the graph of the function:

f(x,y)=-(\cos(x^{2})+\cos(y^{2}))^{2}\,

Generalizations

The graph of a function is contained in a Cartesian product of sets. An X–Y plane is a cartesian product of two lines, called X and Y, while a cylinder is a cartesian product of a line and a circle, whose height, radius, and angle assign precise locations of the points. Fibre bundles are not Cartesian products, but appear to be up close. There is a corresponding notion of a graph on a fibre bundle called a section.

References

^ Charles C Pinter (2014) [1971]. A Book of Set Theory. Dover Publications. p. 49. ISBN 978-0-486-79549-2.
^ T. M. Apostol (1981). Mathematical Analysis. Addison-Wesley. p. 35.
^ P. R. Halmos (1982). A Hilbert Space Problem Book. Springer-Verlag. p. 31. ISBN 0-387-90685-1.
^ D. S. Bridges (1991). Foundations of Real and Abstract Analysis. Springer. p. 285. ISBN 0-387-98239-6.

External links

Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.

[Pinter2014-1] Charles C Pinter (2014) [1971]. A Book of Set Theory. Dover Publications. p. 49. ISBN 978-0-486-79549-2.

[2] T. M. Apostol (1981). Mathematical Analysis. Addison-Wesley. p. 35.

[3] P. R. Halmos (1982). A Hilbert Space Problem Book. Springer-Verlag. p. 31. ISBN 0-387-90685-1.

[4] D. S. Bridges (1991). Foundations of Real and Abstract Analysis. Springer. p. 285. ISBN 0-387-98239-6.

[1]

[2]

[3]

[4]