Geometric terms of location: Difference between revisions
Content deleted Content added
Chris Morath (talk | contribs) m Added links to other articles Tags: Visual edit Mobile edit Mobile web edit Newcomer task Newcomer task: links |
ShelfSkewed (talk | contribs) Links fixes |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Directions or positions relative to the shape and position of an object}} |
{{short description|Directions or positions relative to the shape and position of an object}} |
||
{{Multiple issues| |
{{Multiple issues|{{Unreferenced|date=March 2014}} |
||
{{ |
{{Notability|date=March 2024}}}} |
||
{{Notability|date=March 2024}} |
|||
{{Underlinked|date=March 2024}} |
|||
}} |
|||
'''Geometric terms of location''' describe directions or positions relative to the [[shape]] of an object. These terms are used in descriptions of [[engineering]], [[physics]], and other sciences, as well as ordinary day-to-day discourse. |
'''Geometric terms of location''' describe directions or positions relative to the [[shape]] of an object. These terms are used in descriptions of [[engineering]], [[physics]], and other sciences, as well as ordinary day-to-day discourse. |
||
Though these terms themselves may be somewhat [[Ambiguity|ambiguous]], they are usually used in a context in which their meaning is clear. For example, when referring to a [[drive shaft]] it is clear what is meant by [[axial]] or [[Radial direction|radial directions]]. Or, in a [[free body diagram]], one may similarly infer a sense of orientation by the forces or other [[Vector space|vectors]] represented. |
Though these terms themselves may be somewhat [[Ambiguity|'''ambiguous''']], they are usually used in a context in which their meaning is clear. For example, when referring to a [[drive shaft]] it is clear what is meant by [[axis of rotation|axial]] or [[Radial direction|radial directions]]. Or, in a [[free body diagram]], one may similarly infer a sense of orientation by the forces or [[Otherkin|other]] [[Vector space|vectors]] represented.{{Citation needed|date=March 2024}} |
||
==Examples== |
==Examples== |
||
Common geometric terms of location are: |
Common geometric terms of location are: |
||
[[File:Radial and circumferential roads in Metro Manila.svg|thumb|Radial (solid and colored lines) and circumferential roads (dashed and gray lines) in [[List of roads in Metro Manila|Metro Manila's road network]]]] |
[[File:Radial and circumferential roads in Metro Manila.svg|thumb|Radial (solid and colored lines) and circumferential roads (dashed and gray lines) in [[List of roads in Metro Manila|Metro Manila's road network]]]] |
||
* ''' |
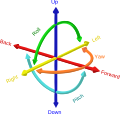
* '''Axial''' – along the center of a round body, or the [[axis of rotation]] of a body |
||
* |
* '''[[Radius|Radial]]''' – along a direction pointing along a [[radius]] from the center of an object, or [[perpendicular]] to a curved path. |
||
* '''[[Circumference|Circumferential]]''' (or '''[[Azimuth|azimuthal]]''') – following around a curve or [[circumference]] of an object. For instance: the pattern of cells in [[Taylor–Couette flow]] varies along the [[azimuth]] of the experiment. |
* '''[[Circumference|Circumferential]]''' (or '''[[Azimuth|azimuthal]]''') – following around a curve or [[circumference]] of an object. For instance: the pattern of cells in [[Taylor–Couette flow]] varies along the [[azimuth]] of the experiment. |
||
* '''[[Tangent|Tangential]]''' – intersecting a curve at a point and parallel to the curve at that point. |
* '''[[Tangent|Tangential]]''' – intersecting a curve at a point and parallel to the curve at that point. |
||
Revision as of 21:14, 7 April 2024
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
|
Geometric terms of location describe directions or positions relative to the shape of an object. These terms are used in descriptions of engineering, physics, and other sciences, as well as ordinary day-to-day discourse.
Though these terms themselves may be somewhat ambiguous, they are usually used in a context in which their meaning is clear. For example, when referring to a drive shaft it is clear what is meant by axial or radial directions. Or, in a free body diagram, one may similarly infer a sense of orientation by the forces or other vectors represented.[citation needed]
Examples
Common geometric terms of location are:

- Axial – along the center of a round body, or the axis of rotation of a body
- Radial – along a direction pointing along a radius from the center of an object, or perpendicular to a curved path.
- Circumferential (or azimuthal) – following around a curve or circumference of an object. For instance: the pattern of cells in Taylor–Couette flow varies along the azimuth of the experiment.
- Tangential – intersecting a curve at a point and parallel to the curve at that point.
- Collinear – in the same line
- Parallel – in the same direction.
- Transverse – intersecting at any angle, i.e. not parallel.
- Orthogonal (or perpendicular) – at a right angle (at the point of intersection).
- Elevation – along a curve from a point on the horizon to the zenith, directly overhead.
- Depression – along a curve from a point on the horizon to the nadir, directly below.
- Vertical – spanning the height of a body.
- Longitudinal – spanning the length of a body.
- Lateral – spanning the width of a body. The distinction between width and length may be unclear out of context.
- Adjacent – next to
- Lineal – following along a given path. The shape of the path is not necessarily straight (compare to linear). For instance, a length of rope might be measured in lineal meters or feet. See arc length.
- Projection / Projected - in architecture, facade sticking out; convex.
- Recession / Recessed - the action of receding; away from an observer; concave.