Dymaxion map

The world on a Dymaxion projection, with 15° graticule

Dymaxion projection with Tissot's indicatrix of deformation

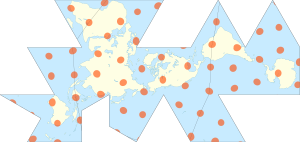
The Dymaxion map projection, also called the Fuller projection, is a kind of polyhedral map projection of the Earth's surface onto the unfolded net of an icosahedron. The resulting map is heavily interrupted in order to reduce shape and size distortion compared to other world maps, but the interruptions are chosen to lie in the ocean.

The projection was invented by Buckminster Fuller. In 1943, Fuller proposed a projection onto a cuboctahedron, which he called the Dymaxion World, using the name Dymaxion which he also applied to several of his other inventions. In 1954, Fuller and cartographer Shoji Sadao produced an updated Dymaxion map, the Airocean World Map, based on an icosahedron with a few of the triangular faces cut to avoid breaks in landmasses.

The Dymaxion projection is intended for representations of the entire Earth.

History

The March 1, 1943, edition of Life magazine included a photographic essay titled "Life Presents R. Buckminster Fuller's Dymaxion World", illustrating a projection onto a cuboctahedron, including several examples of possible arrangements of the square and triangular pieces, and a pull-out section of one-sided magazine pages with the map faces printed on them, intended to be cut out and glued to card stock to make a three-dimensional cuboctahedron or its two-dimensional net. Fuller applied for a patent in the United States in February 1944 for the cuboctahedron projection, which was issued in January 1946.

In 1954, Fuller and cartographer Shoji Sadao produced a new map onto an icosahedron instead of the cuboctahedron. It depicts Earth's continents as "one island", or nearly contiguous land masses. References today to the Fuller projection or Dymaxion usually indicate this version.

Projection of each triangle

Unlike other polyhedral map projections, the Dymaxion map does not use a gnomonic projection (perspective projection through the Earth's center onto the polyhedral surface), which causes length distortion away from the center of each face. Instead each triangle edge of the Dymaxion map matches the scale of a partial great circle on a corresponding globe, and other points within each facet shrink toward its middle. Fuller's 1980 version of the Dymaxion map was the first definition and use of a mathematical transformation process to make the map.

Properties

An icosahedron, the shape the world map is projected onto before unfolding

The world flattens to a Dymaxion map as it unfolds into an icosahedron net with nearly contiguous land masses.

Though neither conformal nor equal-area, Fuller claimed that his map had several advantages over other projections for world maps.

It has less distortion of relative size of areas, most notably when compared to the Mercator projection; and less distortion of shapes of areas, notably when compared to the Gall–Peters projection. Other compromise projections attempt a similar trade-off.

More unusually, the Dymaxion map does not have any "right way up". Fuller argued that in the universe there is no "up" and "down", or "north" and "south": only "in" and "out". Gravitational forces of the stars and planets created "in", meaning "towards the gravitational center", and "out", meaning "away from the gravitational center". He attributed the north-up-superior/south-down-inferior presentation of most other world maps to cultural bias.

Fuller intended the map to be unfolded in different ways to emphasize different aspects of the world. Peeling the triangular faces of the icosahedron apart in one way results in an icosahedral net that shows an almost contiguous land mass comprising all of Earth's continents – not groups of continents divided by oceans. Peeling the solid apart in a different way presents a view of the world dominated by connected oceans surrounded by land.

Showing the continents as "one island earth" also helped Fuller explain, in his book Critical Path, the journeys of early seafaring people, who were in effect using prevailing winds to circumnavigate this world island.

However, the Dymaxion map can also prove difficult to use. It is, for example, confusing to describe the four cardinal directions and locate geographic coordinates. The awkward shape of the map may be counterintuitive to most people trying to use it. For example, the shortest route from Africa to South America is not obvious. Depending on how the map is projected, land masses and oceans are often divided into several pieces.

Conformal variant

In 2019, Daniel "daan" Strebe developed a conformal icosahedral projection, similar to the conformal projections to an octahedron by Oscar S. Adams (1928) and to a tetrahedron by Laurence P. Lee (1965), all three using Dixon elliptic functions. A conformal map preserves angles and local shapes from the sphere at the expense of increasing the scale distortion near the vertices of the icosahedron.

Comparison of the Fuller projection and Strebe's Dymaxion-like
conformal projection with Tissot's indicatrices at 30° intervals

Influence

A 1967 Jasper Johns painting, Map (Based on Buckminster Fuller's Dymaxion Airocean World), depicting a Dymaxion map, hangs in the permanent collection of the Museum Ludwig in Cologne.

The World Game, a collaborative simulation game in which players attempt to solve world problems, is played on a 70-by-35-foot Dymaxion map.

In 2013, to commemorate the 70th anniversary of the publication of the Dymaxion map in Life magazine, the Buckminster Fuller Institute announced the "Dymax Redux", a competition for graphic designers and visual artists to re-imagine the Dymaxion map. The competition received over 300 entries from 42 countries.

The H3 hierarchical global grid implemented by Uber uses an icosahedron oriented in Dymaxion orientation, then further subdivided into hexagons.

In 2020, a collaborative effort by thousands of Minecraft players, the Build the Earth project, used Strebe's conformal variant as a projection for building a 1:1 scale representation of the Earth inside the game.

Gallery

• 
  This icosahedral net shows connected oceans surrounding Antarctica.
• 
  Example of use illustrating early human migrations according to mitochondrial population genetics (numbers are millennia before present)
• 
  Dymaxion map of the world with the 30 largest countries and territories by total area, roughly to scale

See also

• List of map projections
• Authagraph projection, inspired by Fuller, 1999
• Peirce quincuncial projection, 1879
• Polyhedral map projection, earliest known is by Leonardo da Vinci, 1514

External links

• Fuller Map homepage
• Dymaxion Project Animation
• Icosahedron and Fuller maps
• Dynamically generated maps based on the Dymaxion projection