Function (mathematics): Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
---- |
---- |
||
In its most informal sense, a '''function''' is an explicit rule or formula, such as ''f''(''x'') = ''x''<sup>2</sup> or ''f''(''x'',''y'')=''xy'', that converts some input value(s) into another value by substitution into the formula. The input value(s) is often called the ''argument(s)'' of the function; and the resulting output value is often called the value of the function when it is ''evaluated'' at those specific arguments. |
|||
A [[domain]] of a function is the [[set]] from which the input values are taken, and the [[codomain]] of a function is the set to which the output values belong. |
|||
| ⚫ | |||
The [[range]] of a function is the set of all possible output values. |
|||
| ⚫ | |||
| ⚫ | |||
In mathematics, a formula is qualified as a (well-defined) function if the following two conditions are satisfied: |
|||
The formal definition of a function is better than the informal definition. It is because that sometimes mathematicians are not sure whether an "connection" between ''X'' and ''Y'' is really a function, and so the set-theoretic approach gets rid of many logical problems. |
|||
#For each input value, there should only be one possible output value. |
|||
#For each input value, the formula should produce at least one output value in the codomain. |
|||
| ⚫ | |||
To illustrate, consider the following three figures: |
To illustrate, consider the following three figures: |
||
| Line 18: | Line 17: | ||
<tr><td>[[image:notMap1.png]]</td><td> This is not a function in usual sense because 3<small>∈</small>''X'' is associated with two elements ''a'' and ''b'' in ''Y'' (Condition 1 is violated). It is a '''multivalued function'''.</td></tr> |
<tr><td>[[image:notMap1.png]]</td><td> This is not a function in usual sense because 3<small>∈</small>''X'' is associated with two elements ''a'' and ''b'' in ''Y'' (Condition 1 is violated). It is a '''multivalued function'''.</td></tr> |
||
<tr><td>[[image:notMap2.png]]</td><td> This is not a function in usual sense because 1<small>∈</small>''X'' is associated with nothing (Condition 2 is violated). It is a partial function.</td></tr> |
<tr><td>[[image:notMap2.png]]</td><td> This is not a function in usual sense because 1<small>∈</small>''X'' is associated with nothing (Condition 2 is violated). It is a '''partial function'''.</td></tr> |
||
<tr><td>[[image:mathmap.png]]</td><td> This is a (well-defined) function. It can be stated explicitly as |
<tr><td>[[image:mathmap.png]]</td><td> This is a (well-defined) function. It can be stated explicitly as |
||
| Line 24: | Line 23: | ||
:f(x)= { d if x=2 |
:f(x)= { d if x=2 |
||
::\ c if x=3. |
::\ c if x=3. |
||
The range of ''f'' is {a,c,d}. |
|||
</td></tr> |
</td></tr> |
||
</table> |
</table> |
||
The ''[[graph of a function|graph]]'' of a function ''f'' is the collection of all pairs (''x'', ''f''(''x'')) for all ''x'' in ''X''. In our example, the graph of ''f'' is {(1,a),(2,d),(3,c)}. |
|||
==Formal Definition== |
|||
Suppose the domain ''X'' is the set of all married men and the codomain ''Y'' is the set of all married women. The formula <b>''f''(''x'')=the wife of ''x''</b> is clearly not a function. Given a married man ''a'', ''f''(''a'') may either not unique or not exist. In mathematics, it is not a good idea to write down such a fuzzy notation. One way to get around is to consider the formula as the subset of all (husband, wife) pair in ''X''×''Y''. Clearly, if an explicit formula for ''f''(''x'') is really a function, we can still construct the set of pairs ''f''; so nothing is lost by this definition. |
|||
We can then give a precise definition from a [[set theory|set theoretic]] point of view: |
|||
| ⚫ | A function ''f'' with domain ''X'' and codomain ''Y'' (written as ''f'': ''X'' → ''Y'') is a [[subset]] of the [[Cartesian product]] ''X'' × ''Y'' (in other words, ''f'' is a set of ordered pairs {(''x'', ''y'')} with ''x'' in ''X'', ''y'' in ''Y'', often called a [[binary relation]]); with the additional properties that ''f'' is: |
||
| ⚫ | |||
| ⚫ | |||
Notice that the two conditions above are precisely what is needed for the symbol ''f''(''x'') to be defined uniquely for any ''x'' in ''X''. |
|||
If a function ''f'' is defined by specifying it as a binary relation (either directly or indirectly), then we say that ''f'' is ''well defined'' if ''f'' actually satisfies these conditions. We can then write ''f''(''x'') to be the (unique) value ''y'' in ''Y'' which corresponds to the pair (''x'', ''y'') in ''f''; in other words, the statements ''f''(''x'') = ''y'' and (''x'', ''y'') in ''f'' are equivalent. |
|||
| ⚫ | |||
Observe that in set theory there is no distinction between a ''function'' ''f'' and its ''graph''. |
Observe that in set theory there is no distinction between a ''function'' ''f'' and its ''graph''. |
||
| Line 37: | Line 52: | ||
If <var>f</var>: <var>X</var> → <var>Y</var> is a function and <var>A</var> is a [[subset]] of <var>X</var>, then the ''image'' (or ''direct image'') of <var>A</var> under <var>f</var> is the subset of <var>Y</var> defined by |
If <var>f</var>: <var>X</var> → <var>Y</var> is a function and <var>A</var> is a [[subset]] of <var>X</var>, then the ''image'' (or ''direct image'') of <var>A</var> under <var>f</var> is the subset of <var>Y</var> defined by |
||
:<var>f</var>(<var>A</var>) := {<var>f</var>(<var>x</var>) : <var>x</var> in <var>A</var>}. If ''A''=''X'', then ''f''(''X'') is called the ''image'' or ''range'' of ''f''. |
:<var>f</var>(<var>A</var>) := {<var>f</var>(<var>x</var>) : <var>x</var> in <var>A</var>}. |
||
If ''A''=''X'', then ''f''(''X'') is called the ''image'' or ''range'' of ''f''. |
|||
In our example, the image of {2,3} under ''f'' is ''f''({2,3})={c,d} and the image of ''f'' is {a,c,d}. |
In our example, the image of {2,3} under ''f'' is ''f''({2,3})={c,d} and the image of ''f'' is {a,c,d}. |
||
| Line 106: | Line 123: | ||
For example, the relation ''dist'' has the domain <b>R</b> × <b>R</b> and is therefore a [[binary function]]. |
For example, the relation ''dist'' has the domain <b>R</b> × <b>R</b> and is therefore a [[binary function]]. |
||
In that case ''dist''((<var>x</var>,<var>y</var>)) is simply written as ''dist''(<var>x</var>,<var>y</var>). |
In that case ''dist''((<var>x</var>,<var>y</var>)) is simply written as ''dist''(<var>x</var>,<var>y</var>). |
||
==Combining functions== |
|||
The functions <var>f</var>: <var>X</var> → <var>Y</var> and <var>g</var>: <var>Y</var> → <var>Z</var> can be ''composed'' by first applying <var>f</var> to an argument <var>x</var> and then applying <var>g</var> to the result. |
|||
Thus one obtains a function <var>g</var> <sup><small>o</small></sup> <var>f</var>: <var>X</var> → <var>Z</var> defined by (<var>g</var> <sup><small>o</small></sup> <var>f</var>)(<var>x</var>) := <var>g</var>(<var>f</var>(<var>x</var>)) for all <var>x</var> in <var>X</var>. |
|||
As an example, suppose that a plane's height at time <var>t</var> is given by the function <var>h</var>(<var>t</var>) and that the oxygen concentration at height <var>x</var> is given by the function <var>c</var>(<var>x</var>). |
|||
Then (<var>c</var> <sup><small>o</small></sup> <var>h</var>)(<var>t</var>) describes the oxygen concentration around the plane at time <var>t</var>. |
|||
If <var>f</var>: <var>X</var> → <b>R</b> and <var>g</var>: <var>X</var> → <b>R</b> are functions with common domain <var>X</var> and codomain is a [[ring (mathematics)|ring]] <b>R</b>, then one can define the sum function <var>f</var> + <var>g</var>: <var>X</var> → <b>R</b> and the product function <var>f</var> × <var>g</var>: <var>X</var> → <b>R</b> as follows: |
|||
:(<var>f</var> + <var>g</var>)(<var>x</var>) := <var>f</var>(<var>x</var>) + <var>g</var>(<var>x</var>); |
|||
:(<var>f</var> × <var>g</var>)(<var>x</var>) := <var>f</var>(<var>x</var>) × <var>g</var>(<var>x</var>); |
|||
for all <var>x</var> in <var>X</var>. |
|||
This turns the set of all such functions into a ring. |
|||
By taking some other [[abstract algebra|algebraic structure]] <var>A</var> in the place of <b>R</b>, we can turn the set of all functions from <var>X</var> to <var>A</var> into an algebraic structure of the same type in an analogous way. |
|||
Revision as of 23:20, 23 February 2003
This needs to be combined with Function.
In its most informal sense, a function is an explicit rule or formula, such as f(x) = x2 or f(x,y)=xy, that converts some input value(s) into another value by substitution into the formula. The input value(s) is often called the argument(s) of the function; and the resulting output value is often called the value of the function when it is evaluated at those specific arguments.
A domain of a function is the set from which the input values are taken, and the codomain of a function is the set to which the output values belong. The range of a function is the set of all possible output values.
In mathematics, a formula is qualified as a (well-defined) function if the following two conditions are satisfied:
- For each input value, there should only be one possible output value.
- For each input value, the formula should produce at least one output value in the codomain.
To illustrate, consider the following three figures:
| File:NotMap1.png | This is not a function in usual sense because 3∈X is associated with two elements a and b in Y (Condition 1 is violated). It is a multivalued function. |
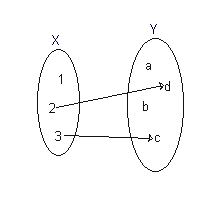 | This is not a function in usual sense because 1∈X is associated with nothing (Condition 2 is violated). It is a partial function. |
| File:Mathmap.png | This is a (well-defined) function. It can be stated explicitly as
The range of f is {a,c,d}. |
The graph of a function f is the collection of all pairs (x, f(x)) for all x in X. In our example, the graph of f is {(1,a),(2,d),(3,c)}.
Formal Definition
Suppose the domain X is the set of all married men and the codomain Y is the set of all married women. The formula f(x)=the wife of x is clearly not a function. Given a married man a, f(a) may either not unique or not exist. In mathematics, it is not a good idea to write down such a fuzzy notation. One way to get around is to consider the formula as the subset of all (husband, wife) pair in X×Y. Clearly, if an explicit formula for f(x) is really a function, we can still construct the set of pairs f; so nothing is lost by this definition.
We can then give a precise definition from a set theoretic point of view:
A function f with domain X and codomain Y (written as f: X → Y) is a subset of the Cartesian product X × Y (in other words, f is a set of ordered pairs {(x, y)} with x in X, y in Y, often called a binary relation); with the additional properties that f is:
- Functional: if there are two pairs (x, y) and (x, z) in f, then y = z.
- Total: for all x in X, there exists an ordered pair (x, y) in f for some y in Y.
Notice that the two conditions above are precisely what is needed for the symbol f(x) to be defined uniquely for any x in X. If a function f is defined by specifying it as a binary relation (either directly or indirectly), then we say that f is well defined if f actually satisfies these conditions. We can then write f(x) to be the (unique) value y in Y which corresponds to the pair (x, y) in f; in other words, the statements f(x) = y and (x, y) in f are equivalent.
Occasionally, especially in the theory of computability, functions as defined here are called total functions to distinguish them from partial functions which don't require condition 2 from above. In this encyclopedia, the terms "total function" and "function" are synonymous.
Observe that in set theory there is no distinction between a function f and its graph. In practice (for example, in analysis) one has the paradoxical situation that the set-theoretic formalism is used, but the language still reflects the classical definition. One rarely talks about functions in terms of the graph. However, considering the properties of the graph as a set can be a very powerful technique, and there are theorems formulated or proved most easily in terms of the graph as a set, such as the closed graph theorem.
Images and preimages
If f: X → Y is a function and A is a subset of X, then the image (or direct image) of A under f is the subset of Y defined by
- f(A) := {f(x) : x in A}.
If A=X, then f(X) is called the image or range of f. In our example, the image of {2,3} under f is f({2,3})={c,d} and the image of f is {a,c,d}.
If B is a subset of Y, we define its preimage (or inverse image) to be the subset of X defined by
- f −1(B) := {x in X : f(x)  in B}.
In our example, the preimage of {a,b} is f −1({a,b})={1}.
Note that the codomain of f -1 is not A, but the set of all subsets of A (also known as the power set of A).
Some consequences that follow immediately from these definitions are:
- f(A1 ∪ A2) = f(A1) ∪ f(A2).
- f(A1 ∩ A2) ⊆ f(A1) ∩ f(A2).
- f −1(B1 ∪ B2) = f −1(B1) ∪ f −1(B2).
- f −1(B1 ∩ B2) = f −1(B1) ∩ f −1(B2).
- f(f −1(B)) ⊆ B.
- f −1(f(A)) ⊇ A.
The results relating images and preimages to the algebra of intersection and union work for any number of sets, not just for 2.
Notice that the range of f is the image f(X) of its domain.
Specifying functions
Functions can be specified in several ways. In practice, most functions that relate (combinations of) numbers with numbers are specified by one or more equation. For example, the dist function can be specified with
- dist(x,y) := (x2 + y2)1/2
or
- z := (x2 + y2)1/2,
where z is called the dependent variable and x and y are called the independent variables. This type of specification is sometimes called specification by intension.
Another way of specifying functions is by specifying the the set of ordered pairs that form the function's graph by either enumerating it or specifying it in set theory. The wght function, for example, might be specified by
- wght := {(Larry,160), (Jimmy,165), (Ruth,125), (Cindy,120), ...}
and nlog might be specified by
- nlog := {(x,y) ∈ R × R : x = ey}.
This type of specification is sometimes also called specification by extension.
A third way of specifying functions that is often used in computer science is specification by computation, where it is indicated how the result of the function is computed from the arguments. An example of this are Lambda expressions in Lambda calculus where the function max(a,b) with a and b integers might be specified as
- max :=
λ (a,b) ∈ Z × Z . if a < b then b else a.
Also recurrences as a way of defining functions.
Injective, surjective and bijective functions
Several types of functions are very useful, deserve special names:
- injective (one-to-one) functions send different arguments to different values; in other words, if x and y are members of the domain of f, then f(x) = f(y) if and only if x = y. Our example is an injective function.
- surjective (onto) functions have their range equal to their codomain; in other words, if y is any member of the codomain of f, then there exists at least one x such that f(x) = y.
- bijective functions are both injective and surjective; they are often used to show that the sets X and Y are "the same" in some sense.
Examples of functions
(More can be found at List of functions.)
- The relation wght between persons in the United States and their weights.
- The relation between nations and their capitals.
- The relation sqr between natural numbers n and their squares n2.
- The relation nlog between positive real numbers x and their natural logarithms ln(x). Note that the relation between real numbers and their natural logarithms is not a function because not every real number has a natural logarithm; that is, this relation is not total and is therefore only a partial function.
- The relation dist between points in the plane R2 and their distances from the origin (0,0).
- The relation grav between a point in the punctured plane R2 \ {(0,0)} and the vector describing the gravitational force that a certain mass at that point would experience from a certain other mass at the origin (0,0).
n-ary function
If the domain of a function is a subset of the Cartesian product of n sets then the function is called an n-ary function. For example, the relation dist has the domain R × R and is therefore a binary function. In that case dist((x,y)) is simply written as dist(x,y).
Combining functions
The functions f: X → Y and g: Y → Z can be composed by first applying f to an argument x and then applying g to the result. Thus one obtains a function g o f: X → Z defined by (g o f)(x) := g(f(x)) for all x in X. As an example, suppose that a plane's height at time t is given by the function h(t) and that the oxygen concentration at height x is given by the function c(x). Then (c o h)(t) describes the oxygen concentration around the plane at time t.
If f: X → R and g: X → R are functions with common domain X and codomain is a ring R, then one can define the sum function f + g: X → R and the product function f × g: X → R as follows:
- (f + g)(x) := f(x) + g(x);
- (f × g)(x) := f(x) × g(x);
for all x in X. This turns the set of all such functions into a ring. By taking some other algebraic structure A in the place of R, we can turn the set of all functions from X to A into an algebraic structure of the same type in an analogous way.
