Function (mathematics)

In mathematics, a function is also called a mapping or a map. Functions are one of the most basic concepts of mathematics, and appear in almost every discipline.

In its most informal sense, a function is an explicit rule or formula, such as f(x) = x² or f(x,y)=xy, that converts some input value(s) into another value by substitution into the formula. The input value(s) is often called the argument(s) of the function; and the resulting output value is often called the value of the function when it is evaluated at those specific arguments.

The domain of a function is the set from which the input values are taken, and the codomain of a function is the set to which the output values belong. The range of a function is the set of all possible output values.

In mathematics, a formula is qualified as a (well-defined) function if the following two conditions are satisfied:

1. For each input value, there should only be one possible output value.
2. For each input value, the formula should produce at least one output value in the codomain.

To illustrate, consider the following three figures:

File:NotMap1.png	This is not a function in usual sense because the element 3 in X is associated with two elements b and c in Y (Condition 1 is violated). It is a multivalued function.
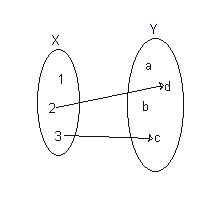	This is not a function in usual sense because the element 1 in X  is associated with nothing (Condition 2 is violated). It is a partial function.
File:Mathmap.png	This is a (well-defined) function. It can be stated explicitly as $f(x)=\left\{{\begin{matrix}a,&{\mbox{if }}x=1\\d,&{\mbox{if }}x=2\\c,&{\mbox{if }}x=3.\end{matrix}}\right.$ The range of f is {a,c,d}.

Formal Definition

The graph of a function f is the collection of all pairs (x, f(x)) for all x in X. In the example above, the graph of f is {(1,a),(2,d),(3,c)}.

More abstractly, the function f(x) = x², where x is any natural number, can be considered as equivalent to the infinite set {(1,1), (2,4), (3,9), (4,16), ...}; and when taken over the real numbers (R), we can consider it equivalent to the uncountable set {(x, x²)}.

By starting with the graph of a function, we can give a precise definition from a set theoretic point of view:

A function f with domain X and codomain Y (written as f: X → Y) is a subset of the Cartesian product X × Y (in other words, f is a set of ordered pairs {(x, y)} with x in X, y in Y, often called a binary relation); with the additional properties that f is:

1. Functional: if there are two pairs (x, y) and (x, z) in f, then y = z.
2. Total: for all x in X, there exists an ordered pair (x, y) in f for some y in Y.

Notice that the two conditions above are precisely what is needed for the symbol f(x) to be defined uniquely for any x in X. If a function f is defined by specifying it as a binary relation (either directly or indirectly), then we say that f is well defined if f actually satisfies these conditions. We can then write f(x) to be the (unique) value y in Y which corresponds to the pair (x, y) in f; in other words, the statements f(x) = y and (x, y) in f are equivalent.

Occasionally, especially in the theory of computability, functions as defined here are called total functions to distinguish them from partial functions which don't require condition 2 from above. In this encyclopedia, the terms "total function" and "function" are synonymous.

One may also consider functions that expect several input values; for instance the volume V of a right circular cone can be computed from the radius r of its base and its height h according to the rule V(r,h) = 1/3 * pi * r² * h. We then consider the domain of V to be the set of ordered pairs of reals (r, h); and we write that V:(R × R) → R.

This definition of function provides mathematicians with a number of useful advantages over the "explicit formula" definition:

• Clearly, if we already have an explicit formula for f(x), we can construct the set of pairs f; so nothing is lost by this definition.
• The definition allows us to consider functions in the abstract which, as a practical matter, could never be evaluated. In particular, functions which would require an infinite number of operations to evaluate can be considered as a set which has been given as a whole, rather than calculated.
• In many cases, there is no explicit formula which amounts to more than a "table" of arguments and values; the above definition accommodates these types of functions naturally.
• We can talk about sets of functions without specifying them exactly; for example, given the domain R of real numbers, and the codomain N of natural numbers, we can talk about the set of all functions of the form f: R → N, or some subset of these functions which satisfy other criteria. Mathematicians are often interested in such generalizations.
• In some cases, it may be unclear whether or not some binary relation f is "truly" a function; the definition provides a way of proving the existence of a well-defined function without actually specifying an explicit formula.

Observe that in set theory there is no distinction between a function f and its graph. In practice (for example, in analysis) one has the paradoxical situation that the set-theoretic formalism is used, but the language still reflects the classical definition. One rarely talks about functions in terms of the graph. However, considering the properties of the graph as a set can be a very powerful technique, and there are theorems formulated or proved most easily in terms of the graph as a set, such as the closed graph theorem.

Images and preimages

If f: X → Y is a function and A is a subset of X, then the image (or direct image) of A under f is the subset of Y defined by

f(A) := {f(x) : x in A}.

If A=X, then f(X) is called the image or range of f. In our example, the image of {2,3} under f is f({2,3})={c,d} and the image of f is {a,c,d}.

If B is a subset of Y, we define its preimage (or inverse image) to be the subset of X defined by

f ⁻¹(B) := {x in X : f(x)&nbsp in  B}.

In our example, the preimage of {a,b} is f ⁻¹({a,b})={1}.

Note that with this definiton, f ^-1 becomes a function whose domain is the set of all subsets of Y (also known as the power set of Y) and whose codomain is the power set of X'.

Some consequences that follow immediately from these definitions are:

• f(A₁ ∪ A₂) = f(A₁) ∪ f(A₂).
• f(A₁ ∩ A₂) ⊆ f(A₁) ∩ f(A₂).
• f ⁻¹(B₁ ∪ B₂) = f ⁻¹(B₁) ∪ f ⁻¹(B₂).
• f ⁻¹(B₁ ∩ B₂) = f ⁻¹(B₁) ∩ f ⁻¹(B₂).
• f(f ⁻¹(B)) ⊆ B.
• f ⁻¹(f(A)) ⊇ A.

The results relating images and preimages to the algebra of intersection and union work for any number of sets, not just for 2.

Notice that the range of f is the image f(X) of its domain.

Specifying functions

Functions can be specified in several ways. In practice, most functions that relate (combinations of) numbers with numbers are specified by one or more equation. For example, the dist function can be specified with

dist(x,y) := (x² + y²)^1/2

or

z := (x² + y²)^1/2,

where z is called the dependent variable and x and y are called the independent variables. This type of specification is sometimes called specification by intension.

Another way of specifying functions is by specifying the the set of ordered pairs that form the function's graph by either enumerating it or specifying it in set theory. The wght function, for example, might be specified by

wght := {(Larry,160), (Jimmy,165), (Ruth,125), (Cindy,120), ...}

and nlog might be specified by

nlog := {(x,y) ∈ R × R : x = e^y}.

This type of specification is sometimes also called specification by extension.

A third way of specifying functions that is often used in computer science is specification by computation, where it is indicated how the result of the function is computed from the arguments. An example of this are Lambda expressions in Lambda calculus where the function max(a,b) with a and b integers might be specified as

max := λらむだ (a,b) ∈ Z × Z . if a < b then b else a.

Functions may also be specified by recursion. The canonical example is the Fibonacci series; we are given that f(1) = 1, f(2) = 1, and the recurrence that for all n>2, f(n) = f(n-1) + f(n-2). The conclusion of the recurrence theorem is that each recurrence there exists a unique function which satisfies the recurrence and the initial conditions.

Injective, surjective and bijective functions

Several types of functions are very useful, deserve special names:

• injective (one-to-one) functions send different arguments to different values; in other words, if x and y are members of the domain of f, then f(x) = f(y) if and only if x = y. Our example is an injective function.
• surjective (onto) functions have their range equal to their codomain; in other words, if y is any member of the codomain of f, then there exists at least one x such that f(x) = y.
• bijective functions are both injective and surjective; they are often used to show that the sets X and Y are "the same" in some sense.

Examples of functions

(More can be found at List of functions.)

• The relation wght between persons in the United States and their weights.
• The relation between nations and their capitals.
• The relation sqr between natural numbers n and their squares n².
• The relation nlog between positive real numbers x and their natural logarithms ln(x). Note that the relation between real numbers and their natural logarithms is not a function because not every real number has a natural logarithm; that is, this relation is not total and is therefore only a partial function.
• The relation dist between points in the plane R² and their distances from the origin (0,0).
• The relation grav between a point in the punctured plane R² \ {(0,0)} and the vector describing the gravitational force that a certain mass at that point would experience from a certain other mass at the origin (0,0).

n-ary function

If the domain of a function is a subset of the Cartesian product of n sets then the function is called an n-ary function. For example, the relation dist has the domain R × R and is therefore a binary function. In that case dist((x,y)) is simply written as dist(x,y).

In abstract algebra, operators such as "*" are defined as binary functions; when we write a formula such as x*y in this context, we are implictly invoking the function *(x,y).

Combining functions

The functions f: X → Y and g: Y → Z can be composed by first applying f to an argument x and then applying g to the result. Thus one obtains a function g o f: X → Z defined by (g o f)(x) := g(f(x)) for all x in X. As an example, suppose that a plane's height at time t is given by the function h(t) and that the oxygen concentration at height x is given by the function c(x). Then (c o h)(t) describes the oxygen concentration around the plane at time t.

If f: X → R and g: X → R are functions with common domain X and codomain is a ring R, then one can define the sum function f + g: X → R and the product function f × g: X → R as follows:

(f + g)(x) := f(x) + g(x);

(f × g)(x) := f(x) × g(x);

for all x in X. This turns the set of all such functions into a ring. By taking some other algebraic structure A in the place of R, we can turn the set of all functions from X to A into an algebraic structure of the same type in an analogous way.

---

In computer science, a function is another common term for subprogram.