User:Harry Princeton/Tiling selection

This is a subset of dual co-uniform tilings by Tomruen which have a particular property, e.g. all clock tilings or all E tilings. Will be ordered by co-uniformity, then by dictionary VRP combination (OSTEIRrDFsCBH), then by wallpaper group.

Tiling Selection

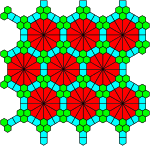
There are 11+20+31+62+140=264 correctly-colored tilings. 🟥🟧🟨🟩🟦🟪🟫⬛⬜

Correctly Colored Tilings

1-Uniform
2-Uniform
3-Uniform
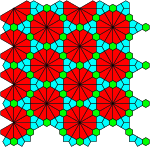
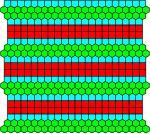
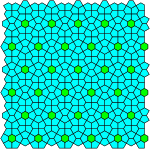
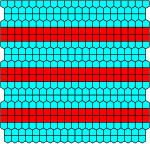
4-Uniform
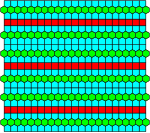
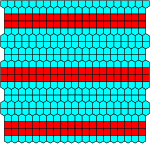
5-Uniform

Difference in versions

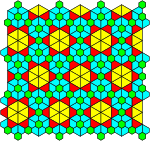
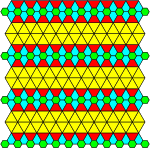
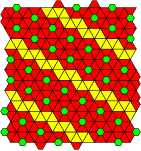
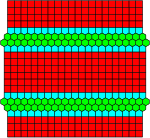
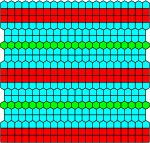
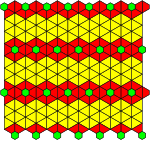
New Tilings
Old Tilings

Other Tilings

Asymmetric Covertex Figure Tilings

The covertex figure is the set of planigons surrounding a covertex, and comprise clocks (12), hexagrams (6), crosses (4), and fidget spinners (3). The floret pentagonal tiling is the only co-uniform tiling with asymmetric fidget spinners. The CB pgg tiling is the only 2 co-uniform tiling with asymmetric crosses. There are four 4-3 tilings with asymmetric hexagrams and one 4-3 with globally asymmetric hexagrams; and two 8-3 tilings with globally asymmetric clocks and one 12-5 tiling with asymmetric clocks. The covertex figures with * are globally asymmetric but (locally) symmetric:

Finally, a tiling with all four types of asymmetric covertex figures (to scale as above):

Clock Tilings

The number of k-co-uniform clock tilings is given by 2, 3, 8, 18, 28, 48, 82, 128, 216, 359, 576, 931, .... While the number of co-uniform tilings more than doubles for each k, the clock subset only increases by 1.65 times each.

There is a 12-co-uniform clock tiling where each clock has no (local) symmetry, but two 8-co-uniform clock tilings where each symmetric clock has no global symmetry. The 11-co-uniform clock tiling represents the interesting family OSTC.

Special Nonslab Clock Tilings

11-Uniform	12-Uniform

Moreover, the other 12-co-uniform clock tiling is singular, up to minor insets of the 3D rhombi, in that it has wallpaper group pmg with 15° axes (e.g., the 3 planigon pairs are 150° apart). (1) the 3D rhombi cannot be elongated because the 45° symmetric (TC)² 4-covertices cannot be (STsB fails). (2) the clocks may not be inset without losing wallpaper symmetry (T is the only planigon allowing 15° axes). (3) the tiling cannot be converted into a cmm variant due to the nature of the (TC)² 4-covertices. (4) clocks cannot be substituted into all 3D rhombi after removing the original clocks due to a 30° offset between adjacent rhombi and co-edge parity.

Trihexagonal Tiling

A strictly trihexagonal tiling consists of vertices with at least one triangle and hexagon and is only made of triangles and hexagons. These vertices are 3².6², (3.6)², 3⁴.6 whose dual planigons are IRF. There exists seven 4-3 tilings:

A trihexagonal tiling consists of vertices with at least one triangle and hexagon, so could contain 3.4².6, 3.4.6.4 as well, with family IRrDF. A unique 12-uniform tiling exists.

A weakly trihexagonal tiling consists of vertices with at least one triangle or hexagon and is only made of triangles and hexagons (so could contain 6³, 3⁶ in addition to the strict case), with family EIRFH. There is one K5 tiling with this family.

Trihexagonal Tiling

Trihexagonal	Weakly Trihexagonal

Every vertex contains at least one triangle or hexagon except for s (4⁴), and there are two 22-13 tilings c.f. optimized tilings.

Orientable Tiling

A tiling is orientable if there exists a 90° rotation such that all of its triangles point up or down (without loss of generality). This entails that all hexagons are in the same orientation, if they exist, and ensures that the tilings are easier to comprehend. Orientable tilings contain all vertices except for 3.4.3.12, 3.4.6.4, 3².4.3.4, or TDC planigons. There are two classes of orientable tilings:

1. Slab tiling – rows of triangles/hexagons separated by rows of squares, spanned by the planigon subset EIRrFsBH. There is a 13-8 tiling with all.
2. Dodecagonal stick – Bosconian-like tilings where trihexagonal regions are bounded by dodecagons and square lengths along the edges corresponding to a larger triangular tiling. These tilings are spanned by the subset 3SEIRrFBH, adding 3S to but removing s from slab tilings.

O is the dodecagonal stick having stick length 0 and the only time it appears in the second class. A 7-uniform dodecagonal stick contains IRF and a 12-uniform one contains EIRFH. Two 16-uniform tilings each contain the whole family.

Orientable Tiling

Slab	Dodecagonal Sticks
13-8	7-Uniform	12-Uniform	16-Uniform	16-Uniform

Planigon Combination

There exist tilings whose planigons are solely semiregular, starting from the Laves planigons themselves: iO3ERDFsCBH.

i (V4.8²) can only exist by itself, O (V3.12²) can only be alone unless with S or T, and E (V6³) is singular without I. This leaves the family 3RDFsCBH. There are exactly 56 combinations of two or more planigons admitting co-uniform tilings from this family, out of 256–8–1=247 total.

Planigon Combinations

3D	RF	DC	DB	FH	sB	CB
CH	BH	3DC	RFB	RFH	DCB	DCH
DBH	FCH	FBH	sCB	sBH	CBH	3DCB
3DCH	RFsB	RFCB	RFBH	DFCB	DFBH	DsCB
DCBH	FsCB	FsBH	FCBH	sCBH	3DsCB	3DCBH
RDFCB	RDFBH	RFsCB	RFsBH	RFCBH	DFsCB	DFCBH
DsCBH	FsCBH	3DFsCB	3DFCBH	3DsCBH	RDFsCB	RDFCBH
RFsCBH	DFsCBH	3RDFsCB	3RDFCBH	3DFsCBH	RDFsCBH	3RDFsCBH

Planigon Cloud

A vertex configuration contains the regular polygons surrounding a vertex, and the planigon cloud is the set of coregular polygons surrounding the planigon. The smallest n-co-uniform tiling required for each largest-area and smallest-area planigon cloud satisfies n≤13, with examples below:

Isolated Planigons

When the planigon cloud does not contain the center planigon, the latter is isolated. No clock planigon may be isolated due to co-edge parity, as is the case with r (3.4².6). The other trapezoid I (3².6²) must be paired whether or not adjacent to E (6³), as any 3-6 edge to 6-6 edge transition about a 6 co-vertex can only be answered by I. In other words, any non-clock non-trapezoid planigon may be isolated.

Affine Linear Expansion Example

Four Cairo pentagons can form an equiangular hexagon cluster. Such a hexagon may be surrounded by a cloud of 1S+3T+1C around each half. Below is the affine linear expansion of a 15-uniform tiling containing these clouds:

Density

In a uniform tiling:

1. The polygonal density is the ratio of number of planigons to number of regular polygons.
2. The edge density is the average length of a dual edge.
3. The area density is the average area of a planigon.

These densities only depend on the distribution of regular polygons and is unaffected by substitutions which preserve the distribution.

$\rho _{\text{poly}}={\frac {n_{3}+2n_{4}+4n_{6}+10n_{12}}{2(n_{3}+n_{4}+n_{6}+n_{12})}}={\frac {2(k_{3}+k_{4}+k_{5}+k_{6})}{k_{3}+2k_{4}+3k_{5}+4k_{6}}}$ where n are regular polygon numbers and k are planigon numbers

A vertex figure containing an s-sided regular polygon corresponds to a planigon which intercepts 1/s of that regular polygon with 1/2–1/s of itself (as edges and dual edges are perpendicular, so only 1–2×1/4=1/2 revolution remains). In other words, each s-sided regular polygon contains equivalent to (1/2–1/s)/(1/s)=(s–2)/2=s/2–1 planigons, for all s, hence the first equality. Likewise, for r-sided planigons, the sum of fractions of regular polygons intercepted must be (r–2)/2=r/2–1 per the sum of angles in any r-sided polygon. The polygonal density is then the reciprocal of the average.

$\rho _{\text{edge}}={\frac {{\sqrt {3}}n_{3}+4n_{4}+6{\sqrt {3}}n_{6}+(24+12{\sqrt {3}})n_{12}}{3n_{3}+4n_{4}+6n_{6}+12n_{12}}}$ (n are regular polygon numbers)

A s-sided regular polygon has an apothem of length ½cot(πぱい/s), which comprises only one of two parts of a dual edge. As each edge is counted twice, the s-sided regular polygon furnishes s/2 edges and s apothems (half dual edges) of combined measure (s/2)cot(πぱい/s). Therefore the individual edge density is (s/2)cot(πぱい/s)÷(s/2)=cot(πぱい/s) but with a relative weight of s (e.g. cot(πぱい/6)=√3 when s=6, hence 6√3 and 6 are included for n₆).

$\rho _{\text{area}}={\frac {{\sqrt {3}}n_{3}+4n_{4}+6{\sqrt {3}}n_{6}+(24+12{\sqrt {3}})n_{12}}{2n_{3}+4n_{4}+8n_{6}+20n_{12}}}$

The area density has the same numerator but different denominator (see the previous remark on edge densities of quadrilaterals as a special case). The area of an s-sided regular polygon is s/2×apothem=(s/2)cot(πぱい/s) but is shared by an equivalent of s/2–1 planigons (from § polygonal density). Therefore, the area per planigon would be (s/2)cot(πぱい/s)÷(s/2–1)=s/(s–2)×cot(πぱい/s) and relatively weighted by s/2–1.

Properties

The polygonal density is the only density that can also depend on the distribution of planigons solely by number of sides. By regular polygon, dodecagon=5, hexagon=2, square=1, triangle=½. By planigon, triangles=2, quadrilaterals=1, pentagons=⅔, hexagons=½.

Since all planigons are tangential with incircle of unit diameter, quadrilateral edge measure is equal to its area. As all quadrilaterals besides s have area exceeding 1, quadrilateral edge density is generally greater than 1 despite having unit polygonal density.

• Setting unit polygonal density implies n₃+4n₆+10n₁₂=2n₃+2n₆+2n₁₂ or n₃=2n₆+8n₁₂.

• Setting unit edge density implies √3n₃+6√3n₆+(24+12√3)d₁₂=3n₃+6n₆+12n₁₂ or (3–√3)n₃=(6√3–6)n₆+(12+12√3)d₁₂ or n₃=2√3n₆+(12+8√3)d₁₂.
• Setting unit area density implies √3n₃+6√3n₆+(24+12√3)d₁₂=2n₃+8n₆+20n₁₂ or (3–√3)n₃=(6√3–8)n₆+(4+12√3)d₁₂ or n₃=(2+4√3)n₆+(44+28√3)d₁₂.

With respect to n₃ the expressions dominates when going down. Thus polygonal>1 → edge>1 → area>1. Interestingly, the latter implication isn't obvious from both sharing the same numerator. Moreover, when the polygonal=1 then edge=area, because the ensuing equality n₃–2n₆–8n₁₂=0 and this expression is the difference between the denominators of area and edge.

Special Tilings

The s tiling has all unit densities and is the only such tiling. On the other extreme, there are three objectives:

1. Maximize edge=area given poly=1.
2. Maximize area and minimize poly given edge=1.
3. Minimize edge and poly given area=1.

All three objectives omit hexagons (n₆=0) as dodecagons have more pull. It remains to minimize n₄ relative to n₁₂ and n₃. This is achieved using double sBH rows interspersed with O swaths for poly=1, and dodecagonal sticks SBH for edge=1 and area=1.

• 
  A 68 co-uniform tiling for which poly=1 and edge=area≈1.5001, exceeding 1½.
• 
  Left: a 3 co-uniform tiling for which poly=8/11, edge≈0.9984, area≈1.1856. Right: a 7 co-uniform tiling for which poly=11/18, edge≈0.75900, area≈1.0005.

Substitution

Further information: Planigon § Insets of Dual Planigons into Higher Degree Vertices

Substitution in a uniform tiling happens when replacing a cluster of regular polygons with another cluster that occupies the same combined shape. From left to right, up to down:

1. Inset rolling — deltoidal hexagons are rotated 90°.
2. (Dual of) Alternating between the two p6 configurations of six hexagons and twelve triangles within a hexagon of side length 3.
3. Placing clocks in the two possible configurations within parallel chains of deltoidal hexagons.
4. (Dual of) Increasing the central hexagonal bubbles within a rhombille web otherwise made of square lengths and triangle corners.
5. Semi-fractalization — the planigons EIRFH may correspond to larger regions modified from rhombille web tilings if the number of 4 co-vertices along the web's edges is a multiple of 3.
6. Full inset — all clocks are inset by deltoidal hexagons D, then all hexagrams are inset by hexagons H.
7. Placing clock(s) in the two possible configurations within chains of three deltoidal hexagons.
8. (Dual of) Six hexagons either adjacent to the center dodecagon or the six apothem dodecagons, all within a hexagonal formation of 12 edge-to-edge dodecagons, and filling the rest with squares and triangles.
9. A seven clock swath where each clock shares edges or a single vertex with adjacent clocks (e.g. only 3 has the latter property), within a predetermined boundary.

All-Edge Tiling

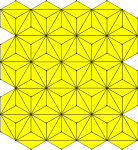
There are 12 types of edges in a co-uniform tiling, of which 10 exist outside a singular case (i or 4.8²). The edges are 3–3, 3–4, 3–6, 3–12, 4–4, 4–6, 4–12, 6–6, 6–12, 12–12.

Only O contains 12–12, only 3 contains 6–12. Since E must be paired with I, it is advantageous to use I only for 6–6. Any tiling with O3I necessarily contains the remaining edges (and S must bridge between O and 3).

A 6–12 adjacent to a 6–6 must be at least 120° away from the 12–12, otherwise the minimal trihexagonal region containing 6–6 will conflict with the two dodecagons. A120° separation admits a 18-uniform tiling with a trihexagonal region and elongated triangular borders (with a 180° separation as well). A 150° separation admits a 23-uniform tiling with two types of trihexagonal bubbles. But a 180° separation admits a 12-uniform tiling c.f. planigon.

All-Edge Tiling Examples

3 Cases	12-Uniform

n-Gonal subset

A 17-11 tiling contains all triangles O3E, a 20-11 tiling contains all quadrilaterals STIRrDs, and a K3 tiling contains all pentagons FCB. Finally, a K7 tiling contains all demiregular planigons.

Tilings containing all plangions of a given type

Triangle	Quadrilateral	Pentagon	Demiregular

Elongating the hexagonal borders of the triangle tiling yields the quadrilateral tiling (s replacing O), and both are derived from the 22-13 tilings c.f. planigon.

Further information: Pentagonal tiling § Dual uniform tilings

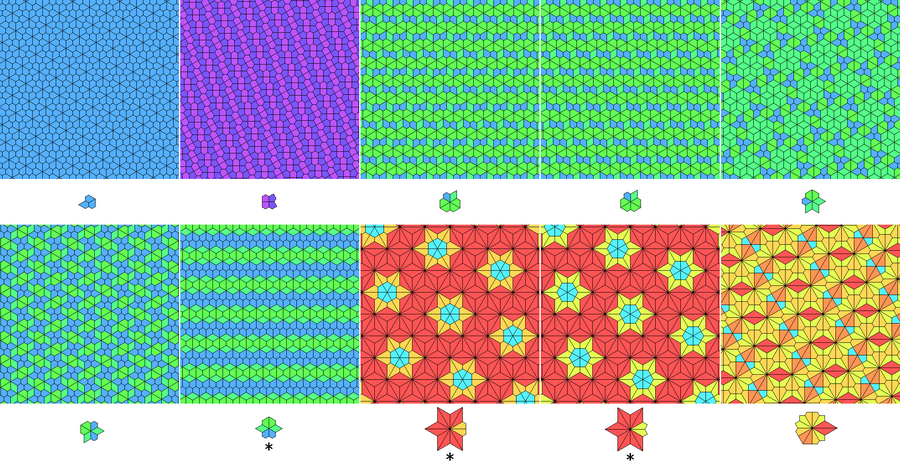
There are infinitely many pentagonal tilings with CB (3².4.3.4, 3³.4²). One subfamily adds any number of 15°-slanted columns of Cairo pentagons between 15°-slanted stacks of Barn pentagons, with a 6-uniform example with wallpaper pg. Since neither FC nor FB can tile alone (nonetheless rFC and FBH are admissible), the remaining family is FCB (3⁴.6, 3².4.3.4, 3³.4²), which in fact has infinite size.

F necessarily occurs in flower-like clusters of 6, surrounded by 6 Cairos and 6 Barns, within an "FCB hexagon" of side length 2+1/√3. There exists a 3, 5, 9, 11, 12-uniform pentagonal tiling with FCB, all with wallpaper p6m, and 8-uniform with p6. Connecting the FCB hexagons with edges form triangular tilings of various edge length. Making the 5-uniform and 11-uniform triangular edges perpendicular generates an infinite FCB family isomorphic to the class of EIR tilings (minus its radial subset), where the 5-uniform edge corresponds to the √3 unit edge of E and the 11-uniform edge corresponds to the 2 unit diagonal of R. This can also be applied to the 9-uniform and 12-uniform triangular edges for another infinite family. One example from each is shown below, corresponding to the 2-uniform IR and 4-uniform EIR with wallpaper cmm, respectively:

Pentagonal Tilings

6-Uniform	FCB (18-Uniform)	FCB (82-Uniform)