User:Tomruen/monogon
| Henagon | |
|---|---|
 On a circle, a henagon is a tessellation with a single vertex, and one 360-degree arc. | |
| Type | Regular polygon |
| Edges and vertices | 1 |
| Schläfli symbol | {1} |
| Coxeter–Dynkin diagrams | |
| Dual polygon | Self-dual |
In geometry a henagon (or monogon) is a polygon with one edge and one vertex. It has Schläfli symbol {1}. Since a henagon has only one side and only one vertex, every henagon is regular by definition.
In Euclidean geometry
[edit]In Euclidean geometry a henagon is usually considered to be an impossible object, because its endpoints must coincide, unlike any Euclidean line segment. For this reason, most authorities do not consider the henagon as a proper polygon in Euclidean geometry.
In spherical geometry
[edit]In spherical geometry, a finite henagon can be drawn by placing a single vertex anywhere on a great circle. This forms a henagonal dihedron (Schläfli symbol {1,2}), with two hemispherical henagonal faces which share one 360° edge and one vertex. Its dual {2,1}, the henagonal hosohedron, has one digonal face (a full 360° lens), one 180° edge, and two vertices.
Simplest of all, the henagonal henahedron {1,1} is similar to the henagon but consists of a single vertex on the sphere, no edges and a single face as the sphere outside the vertex. The henagonal henahedron is self-dual, i.e. the point and face center can be swapped creating itself as a central inversion.
| Henagonal dihedron | Henagonal hosohedron Digonal henahedron |
Henagonal henahedron |
|---|---|---|
| Dual tilings | Self-dual | |
 {1,2} |
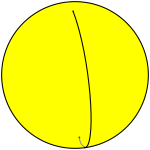 {2,1} |
 {1,1} |
| (F:2, E:1, V=1) | (F:1, E:1, V=2) | (F:1, E:0, V=1) |
See also
[edit]References
[edit]- Olshevsky, George. "Monogon". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Herbert Busemann, The geometry of geodesics. New York, Academic Press, 1955
