Contacto rueda-carril

Rueda del Shinkansen

Esquema del contacto rueda-carril

El contacto rueda-carril es el área donde tiene lugar la interacción entre ruedas y raíles en los ferrocarriles.​ Esta interacción es un tema especializado que cubre la modelización de las elevadas tensiones mecánicas que se producen en la pequeña área de contacto entre una rueda de acero y un raíl de acero.

Su propósito se centra en la mejora de la seguridad, la reducción de los costos de mantenimiento y sustitución, la reducción del tiempo de inactividad y la gestión de la energía y del medio ambiente.​​ La superficie de la rueda que descansa sobre el raíl se conoce como la banda de rodadura. Las ruedas pueden tener una sola pestaña en el lado interior del riel, o dos pestañas, una a cada lado.

Historia

La mecánica del contacto entre la rueda y el carril en su forma moderna fue estudiada a partir de la década de 1990 por el ingeniero neerlandés Coenraad Esveld, que aplicó un modelo elástico basado en la teoría de Hertz (que lleva el nombre del físico alemán Heinrich Hertz (1857-1894), mucho más conocido por su descubrimiento de las ondas hertzianas). Esta teoría permite modelizar el comportamiento de las deformaciones experimentadas entre dos sólidos sometidos a una carga de compresión. Esveld analizó la forma en la que se equilibra la carga vertical aplicada sobre una rueda, y concluyó que en la zona de contacto con el carril se genera una fuerza de reacción elástica que se traduce en la formación de una huella con forma elíptica, en la que físicamente ambas superficies están en contacto real, y por lo tanto, es posible cuantificar las tensiones y el rozamiento efectivo movilizado en la citada superficie de contacto.​

Caracterización mecánica

Distintas localizaciones y configuraciones de las formas elípticas del contacto entre rueda y carril

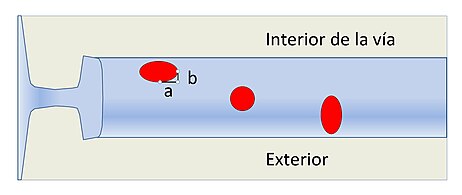
Las elipses de contacto tienen habitualmente tamaños del orden de 2 o 3 cm, y sus dimensiones están condicionadas tanto por la geometría de la zona de contacto, como por las cargas soportadas y por las características mecánicas del acero de ambos elementos. La geometría de los perfiles del carril y de la llanta de la rueda suelen ser complementarios, y están configurados mediante la combinación de un conjunto de varios arcos circulares consecutivos de distinto radio.

Según Esveld, la tensión media total en la zona de contacto entre rueda y carril está relacionada directamente con la carga vertical $Q$ soportada por la rueda y con la superficie de la huella elíptica formada ($\pi ab$), y viene dada por la expresión:​

[1] $\sigma _{\text{(media T)}}={\frac {3}{2}}{\frac {Q}{\pi ab}}$

lo que implica que la tensión total media resultante es vez y media (3/2 veces) la tensión necesaria para garantizar el equilibrio vertical de fuerzas (es decir, la tensión media en la huella σしぐま=Q/Πぱいab necesaria para equilibrar el peso aplicado sobre la rueda). Lógicamente, el grado de deformación del contacto rueda carril en la huella no es uniforme, y cuanto más cerca se esté del borde de la elipse, más se acerca a cero. Este incremento de la tensión media es debido a la aparición de componentes longitudinales y transversales respecto al eje de la vía, que contribuyen al reequilibrio del sistema de fuerzas alterado por la deformación elástica de la zona de contacto.

Para el cálculo de la tensión media vertical generada en el carril exclusivamente por las fuerzas verticales, Esveld dedujo la siguiente fórmula:​

[2] $\sigma _{\text{(media v)}}={\sqrt {{\frac {\pi E}{64(1-\nu ^{2})}}{\frac {Q}{rb}}}}=C{\sqrt {\frac {Q}{r}}}$

donde (entre paréntesis, se indican las unidades y los valores usuales de estos parámetros):

$Q$ = carga vertical soportada por la rueda (en newtons)

$r$ = radio de la rueda (en metros)

$b$ = semiancho de la huella de contacto elíptica (en metros)

$E$ = módulo de elasticidad del acero (2.1·10¹¹ N/m²)

$\nu$ = coeficiente de Poisson del acero (0.3)

Como se aprecia en la última expresión, para agilizar los cálculos los términos fijos se pueden agrupar en una constante denominada $C$, haciendo depender el resultado únicamente de la raíz del cociente $Q/r$.

Valores característicos

Tensiones en el contacto rueda carril​

Radio Rueda (mm)	Radio Perfil Rueda (mm)	Radio Perfil Carril (mm)	a (mm)	b (mm)	[1] σしぐま(media T) (N/mm²)	[2] σしぐま(media v) (N/mm²)	Contacto (2ax2b)
460	∞	300	6.1	4.7	1012	686
460	-330	300	3.9	14.6	502	389
460	-330	80	7.1	2.7	1520	905
150	-330	80	4.2	3.3	2103	1434
Carga vertical $Q$ sobre la rueda: 90 kN

En la tabla adjunta figuran diversos ejemplos de la configuración de la huella del contacto entre rueda y carril, en el que se especifican la geometría de la rueda y del carril, las dimensiones de la elipse resultante, la tensión media total y la tensión media vertical (calculada esta última según la fórmula [2]). Se trata de ejemplos prácticos ligados a parámetros reales, en los que se puede visualizar la correlación antes indicada de que

$\sigma _{\text{(media T)}}={\frac {3}{2}}\sigma _{\text{(media v)}}$

En los casos reflejados en la tabla,​ la carga $Q$ considerada sobre la rueda es del orden de 90 kilonewtons, correspondientes a unas 18 toneladas de peso sobre un eje de dos ruedas.

Con el objeto de asimilar el comportamiento del contacto rueda carril a un resorte de constante de elongación $k_{h}$, Esveld utilizó una tercera fórmula, valiéndose de la expresión de Grassie​ (debida al ingeniero británico Stuart L. Grassie), que toma la forma:

[3] $k_{h}={\sqrt[{3}]{\frac {3E_{\text{carril}}^{2}Q{\sqrt {R_{\text{rueda}}R_{\text{carril}}}}}{2(1-\nu ^{2})^{2}}}}$

donde (entre paréntesis, se indican las unidades y los valores usuales de estos parámetros):

$E$ = módulo de elasticidad del acero (2.1·10¹¹ N/m²)

$R_{\text{rueda}}$ = Radio de la rueda (habitualmente 0.42 metros)

$R_{\text{carril}}$ = Radio del carril (habitualmente 0.30 metros para el carril UIC 54)

$\nu$ = coeficiente de Poisson del acero (0.3)

$Q$ = carga vertical estática soportada por una rueda (habitualmente 100.000 newtons)

Utilizando estos valores, se obtiene que el módulo de deformación equivalente del contacto rueda carril $k_{h}=1.407\;10^{9}N/m=1407\;kN/mm$. En términos de la mecánica de un muelle, se puede concluir que el contacto rueda carril posee una enorme rigidez, dado que el valor calculado de $k_{h}$ implica que para deformar 1 mm el carril, es necesario aplicar sobre la rueda un peso de 140 toneladas. Con las cargas habituales, del orden de 10 toneladas por rueda, las deformaciones de carácter elástico en la zona de contacto pasan a ser de menos de una décima de milímetro.

Véase también

• Adherencia rueda-carril
• Movimiento de lazo

Referencias

• Datos: Q16969080