Cuboctaedro cubitruncado
| Cuboctaedro cubitruncado | ||
|---|---|---|
 | ||
 Modelo 3D | ||
| Tipo |
icosaedro, poliedro uniforme y poliedro no convexo | |
| Forma de las caras |
octógono regular (6) octagrama (6) hexágono regular (8) | |
| Configuración de vértices |
triángulo | |
| Dual |
tetradiaquis hexaedro | |
| Elementos | ||
| Vértices | 48 | |
| Aristas | 72 | |
| Caras | 20 | |
| Más información | ||
| MathWorld |
CubitruncatedCuboctahedron | |
En geometría, el cuboctaedro cubitruncado o cuboctaedro cuboctatruncado es un poliedro uniforme estrellado, indexado como U16. Tiene 20 caras (8 hexágonos, 6 octógonos y 6 octagramas), 72 aristas y 48 vértices;[1] y su símbolo de Shäfli es tr{4,3/2}.
Envolvente convexa
[editar]Su envolvente convexa es un cuboctaedro truncado no uniforme.
 Envolvente convexa |
 Cuboctaedro cubitruncado |
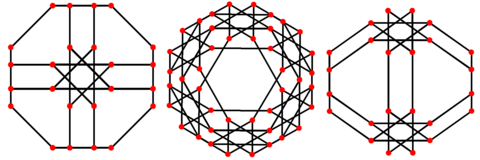
Proyecciones ortogonales
[editar]Coordenadas cartesianas
[editar]Las coordenadas cartesianas de los vértices de un cuboctaedro cubitruncado son todas las permutaciones de
- (±(√2−1), ±1, ±(√2+1))
Poliedros relacionados
[editar]Tetradiaquis hexaedro
[editar]| Tetradiaquis hexaedro | ||
|---|---|---|
 Imagen del sólido | ||
| Tipo | Poliedro estrellado | |
| Caras |
48 | |
| Aristas | 72 | |
| Vértices | 20 | |
| Grupo de simetría | Oh, [4,3], *432 | |
| Poliedro dual | Cuboctaedro cubitruncado | |

El tetradiaquis hexaedro (o gran disdiaquis dodecaedro) es un poliedro no convexo isoeedral. Posee 48 caras triangulares que se cruzan, 72 aristas y 20 vértices.
Proporciones
[editar]Los triángulos tienen un ángulo de , uno de y uno de . Su ángulo diedro es igual a . Parte de cada triángulo se encuentra dentro de la figura, por lo que es invisible en los modelos sólidos.
Es el dual del cuboctaedro cubitruncado uniforme.
Véase también
[editar]Referencias
[editar]- ↑ Maeder, Roman. «16: cubitruncated cuboctahedron». MathConsult. Archivado desde el original el 29 de marzo de 2015.
Bibliografía
[editar]- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208. pág.92
Enlaces externos
[editar]- Weisstein, Eric W. «Cubitruncated cuboctahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Tetradyakis hexahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- http://gratrix.net Poliedros uniformes y duales