Diagrama de Coxeter-Dynkin

En geometría, un diagrama de Coxeter-Dynkin (también diagrama de Coxeter o gráfico de Coxeter) es un grafo con enlaces etiquetados s (o hiperplanos reflectores). Describe una construcaleidoscópica: ca dominio de una faceta) y la etiqueta ligada a una rama codifica el orden del ángulo diedro entre cada dos espejos (en un dominio de una cara), es decir, la cantidad por la que se tiene que multiplicar el ángulo entre los planos reflectantes para obtener 180 grados. Una rama sin etiquetar representa implícitamente el orden 3 (60 grados).

Cada diagrama representa un grupo de Coxeter, que se clasifican por sus diagramas asociados.

Los diagramas de Dynkin son objetos estrechamente relacionados, que difieren de los diagramas de Coxeter en dos aspectos: en primer lugar, las ramas etiquetadas como "4" o mayores están dirigidas, mientras que los diagramas de Coxeter son no dirigidos; en segundo lugar, los diagramas de Dynkin deben satisfacer una restricción adicional (la restricción cristalográfica), a saber, que las únicas etiquetas de rama permitidas son 2, 3, 4 y 6. Los diagramas de Dynkin guardan una correspondencia directa con los sistemas raíz, por lo que se usan para clasificarlos. Esto implica a su vez que forman álgebras de Lie semisimples.^[1]

Descripción

Las ramas de un diagrama de Coxeter-Dynkin están etiquetadas con un número racional p, que representa un ángulo diedro de 180°/p. Cuando $p = 2$ el ángulo es de 90° y los espejos no tienen interacción, entonces la rama puede omitirse del diagrama. Si una rama no está etiquetada, se supone que tiene $p = 3$ , que representa un ángulo de 60°. Dos espejos paralelos tienen una rama marcada con "∞". En principio, los n espejos pueden representarse mediante un grafo completo en el que se dibujan todas las $n (n - 1) / 2$ ramas. En la práctica, casi todas las configuraciones interesantes de los espejos incluyen varios ángulos rectos, por lo que debe tenerse en cuenta que las ramas correspondientes se omiten.

Los diagramas se pueden etiquetar por su estructura gráfica. Las primeras formas estudiadas por Ludwig Schläfli son los ortoesquemas, que poseen gráficos lineales que generan politopos regulares y panales regulares. Los plagioesquemas son símplex representados por gráficos ramificados, y los cicloesquemas son símplex representados por gráficos cíclicos.

Matriz de Schläfli

Cada diagrama de Coxeter tiene su correspondiente matriz de Schläfli (llamada así por Ludwig Schläfli), con elementos de matriz $a i,j = a j,i = -2cos (π ぱい / p)$ , donde p es el orden de las ramas entre los pares de espejos. Al igual que una matriz de cosenos, también se denomina matriz de Gram, en referencia al matemático danés Jørgen Pedersen Gram (1850-1916). Todas las matrices de Schläfli del grupo de Coxeter son simétricas porque sus vectores raíz están normalizados. Se relaciona estrechamente con la matriz de Cartan, utilizada en los diagramas de Dynkin, gráficos similares (aunque dirigidos) en los casos limitados a p = 2,3,4 y 6, que NO son simétricos en general.

El determinante de la matriz de Schläfli (llamado schläfliano) y su signo determinan si el grupo es finito (positivo), afín (cero), o indefinido (negativo). Esta regla se llama criterio de Schläfli.^[2]

Los autovalores de la matriz de Schläfli determinan si un grupo de Coxeter es de tipo finito (todo positivo), tipo afín (todo no negativo, y al menos uno es cero) o tipo indefinido (de otra manera). El tipo indefinido a veces se subdivide aún más, en hiperbólicos y otros grupos de Coxeter. Sin embargo, existen múltiples definiciones no equivalentes para los grupos hiperbólicos de Coxeter. Se usa la siguiente definición: un grupo de Coxeter con diagrama conectado es hiperbólico si no es de tipo finito ni afín, pero cada subdiagrama conectado es de tipo finito o afín. Un grupo de Coxeter hiperbólico es compacto si todos los subgrupos son finitos (es decir, tienen determinantes positivos) y paracompacto si todos sus subgrupos son finitos o afines (es decir, tienen determinantes no negativos).

Los grupos finitos y afines también se denominan elípticos y parabólicos respectivamente. Los grupos hiperbólicos también se llaman grupos de Lannér, en referencia a F. Lannér, que enumeró los grupos hiperbólicos compactos en 1950,^[3] y también grupos de Koszul (o cuasi-Lannér) para los grupos paracompactos.

Grupos de Coxeter de rango 2

Para el rango 2, el tipo de un grupo Coxeter está completamente fijado por el determinante de la matriz de Schläfli, ya que es simplemente el producto de sus valores propios: tipo finito (determinante positivo), tipo afín (determinante cero) o hiperbólico (determinante negativo). Coxeter usa una notación de corchetes equivalente, que enumera las secuencias de órdenes de ramas como un sustituto de los diagramas gráficos de ramas y nodos. También existen soluciones racionales [p/q], , con máximo común divisor (p, q) = 1, que definen dominios fundamentales superpuestos. Por ejemplo, 3/2, 4/3, 5/2, 5/3, 5/4. y 6/5.

Tipo	Finito					Afín	Hiperbólico
Geometría					...
Coxeter	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπぱい/λらむだ]
Orden	2	4	6	8	2p	∞
Los ejes de simetría especular están coloreados para corresponder con los nodos del diagrama de Coxeter. Los dominios fundamentales están coloreados alternativamente

Diagramas de grupos de Coxeter de rango 2
Orden p	Grupo	Diagrama de Coxeter		Matriz de Schläfli
Orden p	Grupo	Diagrama de Coxeter		$\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]$	Determinante (4-a₂₁*a₁₂)
Finito (Determinante>0)
2	I₂(2) = A₁xA₁		[2]	$\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]$	4
3	I₂(3) = A₂		[3]	$\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]$	3
3/2			[3/2]	$\left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]$	3
4	I₂(4) = B₂		[4]	$\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]$	2
4/3			[4/3]	$\left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]$	2
5	I₂(5) = H₂		[5]	$\left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]$	$(5-{\sqrt {5}})/2$ ~1.38196601125
5/4			[5/4]	$\left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]$	$(5-{\sqrt {5}})/2$ ~1.38196601125
5/2			[5/2]	$\left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]$	$(5+{\sqrt {5}})/2$ ~3.61803398875
5/3			[5/3]	$\left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]$	$(5+{\sqrt {5}})/2$ ~3.61803398875
6	I₂(6) = G₂		[6]	$\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]$	1
6/5			[6/5]	$\left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]$	1
8	I₂(8)		[8]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {2}}}}\\-{\sqrt {2+{\sqrt {2}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {2}}$ ~0.58578643763
10	I₂(10)		[10]	$\left[{\begin{smallmatrix}2&-{\sqrt {(5+{\sqrt {5}})/2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{smallmatrix}}\right]$	$(3-{\sqrt {5}})/2$ ~0.38196601125
12	I₂(12)		[12]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {3}}}}\\-{\sqrt {2+{\sqrt {3}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {3}}$ ~0.26794919243
p	I₂(p)		[p]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /p)$
Afín (Determinante=0)
∞	I₂(∞) = ${\tilde {I}}_{1}$ = ${\tilde {A}}_{1}$		[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
Hiperbólico (Determinante≤0)
∞			[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
∞			[iπぱい/λらむだ]	$\left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]$	$-4\sinh ^{2}(2\lambda )\leq 0$

Visualizaciones geométricas

El diagrama de Coxeter-Dynkin puede verse como una descripción gráfica del dominio fundamental de los espejos. Un espejo representa un hiperplano dentro de un espacio euclídeo, esférico o hiperbólico de una dimensión dada. En espacios 2D, un espejo es una recta, y en 3D un espejo es un plano.

Estas visualizaciones muestran los dominios fundamentales para grupos euclídeos 2D y 3D, y grupos esféricos 2D. Para cada uno, el diagrama de Coxeter puede deducirse identificando los espejos del hiperplano y etiquetando su conectividad, ignorando los ángulos diédricos de 90 grados (orden 2).

Grupos de Coxeter en el plano euclídeo con sus diagramas equivalentes. Las reflexiones se etiquetan como nodos gráficos R1, R2, etc. y se colorean por su orden de reflexión. Las reflexiones a 90 grados están inactivas y, por lo tanto, se suprimen del diagrama. Las simetrías especulares paralelas están conectadas por una rama etiquetada con ∞. El grupo prismático ${\tilde {I}}_{1}$ x ${\tilde {I}}_{1}$ se muestra como una duplicación de ${\tilde {C}}_{2}$ , pero también se puede crear en forma de dominios rectangulares al duplicar los triángulos ${\tilde {G}}_{2}$ . ${\tilde {A}}_{2}$ es una duplicación del triángulo ${\tilde {G}}_{2}$ .
Muchos grupos de Coxeter en geometría hiperbólica pueden extenderse de los casos euclídeos como una serie de soluciones hiperbólicas.
Grupos de Coxeter en el espacio 3d con sus diagramas. Los espejos (caras triangulares) están etiquetados por el vértice opuesto 0..3. Las ramas se colorean por su orden de reflexión. ${\tilde {C}}_{3}$ llena 1/48 del cubo. ${\tilde {B}}_{3}$ llena 1/24 del cubo. ${\tilde {A}}_{3}$ llena 1/12 del cubo.	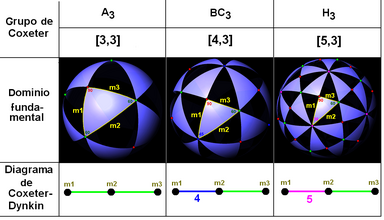Grupos de Coxeter en la esfera, con sus diagramas equivalentes. El dominio fundamental se describe en amarillo. Los vértices del dominio (y las ramas del gráfico) están coloreados por su orden de reflexión.

Grupos de Coxeter finitos

Véase también familias de politopos para obtener una tabla de los politopos uniformes de nodo final asociados con estos grupos.

Se utilizan indistintamente tres simbologías diferentes para definir los mismos grupos: como una letra/número, como un conjunto de números entre corchetes y como el diagrama de Coxeter.
Los grupos D_n bifurcados son versiones semi o alternadas de los grupos C_n regulares.
Los grupos bifurcados D_n y E_n también están etiquetados con un superíndice [3^a,b,c] donde a, b, y c son los números de segmentos en cada una de las tres ramas.

Diagramas de Coxeter-Dynkin finitos conectados (rangos de 1 a 9)
Rank	Grupos de Lie simples			Grupos de Lie excepcionales
Rank	${A}_{1+}$	${B}_{2+}$	${D}_{2+}$	${E}_{3-8}$	${F}_{3-4}$	${G}_{2}$	${H}_{2-4}$	${I}_{2}(p)$
1	A₁=[ ]
2	A₂=[3]	B₂=[4]	D₂=A₁A₁			G₂=[6]	H₂=[5]	I₂[p]
3	A₃=[3²]	B₃=[3,4]	D₃=A₃	E₃=A₂A₁	F₃=B₃		H₃
4	A₄=[3³]	B₄=[3²,4]	D₄=[3^1,1,1]	E₄=A₄	F₄		H₄
5	A₅=[3⁴]	B₅=[3³,4]	D₅=[3^2,1,1]	E₅=D₅
6	A₆=[3⁵]	B₆=[3⁴,4]	D₆=[3^3,1,1]	E₆=[3^2,2,1]
7	A₇=[3⁶]	B₇=[3⁵,4]	D₇=[3^4,1,1]	E₇=[3^3,2,1]
8	A₈=[3⁷]	B₈=[3⁶,4]	D₈=[3^5,1,1]	E₈=[3^4,2,1]
9	A₉=[3⁸]	B₉=[3⁷,4]	D₉=[3^6,1,1]
10+	..	..	..	..

Aplicación con politopos uniformes


Al construir politopos uniformes, los nodos se marcan como "activos" mediante un anillo si un punto generador está fuera del espejo, creando una nueva arista entre un punto generador y su imagen reflejada. Un nodo sin anillo representa un espejo "inactivo", que no genera puntos nuevos.	Se pueden usar dos espejos ortogonales para generar un cuadrado, , visto aquí con un punto generador rojo y 3 copias virtuales a través de los espejos. El generador tiene que estar fuera de ambos espejos en este caso ortogonal para generar un interior. El marcado del anillo supone que los anillos activos tienen generadores a la misma distancia de todos los espejos, mientras que un rectángulo también puede representar una solución no uniforme.

Los diagramas de Coxeter-Dynkin pueden enumerar explícitamente casi todas las clases de politopos uniformes y de teselados uniformes. Cada politopo uniforme con simetría reflexiva pura (todos, menos algunos casos especiales, tienen simetría reflexiva pura) puede representarse mediante un diagrama de Coxeter-Dynkin con permutaciones de "márgenes". Cada politopo uniforme puede generarse usando tales espejos y un único punto generador: las imágenes especulares crean nuevos puntos como reflejos, y entonces se pueden definir las aristas del polítopo como segmentos entre cada punto y sus imágenes en los espejos. Las caras se generan por el reflejo repetido de las aristas que finalmente envuelven al generador original; la forma final, así como las facetas de dimensiones superiores, también se crean cuando la cara se refleja para encerrar un área.

Para especificar los vértices generadores, se marcan uno o más nodos con anillos, lo que significa que el vértice no está en el espejo(s) representado por el nodo(s) anillado (si se marcan dos o más espejos, el vértice es equidistante de ellos). Un espejo está "activo" (crea reflejos) solo con respecto a los puntos que no están en él. Un diagrama necesita al menos un nodo activo para representar un politopo. Un diagrama no conectado (subgrupos separados por ramas de orden 2 o espejos ortogonales) requiere al menos un nodo activo en cada subgrafo.

Todos los politopos regulares, representados por los símbolos de Schläfli { $p, q, r, ...$ }, pueden tener sus dominios fundamentales representados por un conjunto de n espejos con un diagrama de Coxeter-Dynkin relacionado con una línea de nodos y ramas etiquetadas por $p, q, r, ...,$ con el primer nodo anillado.

Los politopos uniformes con un anillo corresponden a puntos generadores en las esquinas del dominio fundamental simplex. Dos anillos corresponden a los bordes de simplex y tienen un grado de libertad, con solo el punto medio como la solución uniforme para longitudes de arista iguales. En general, los k puntos generadores con anillo están situados sobre las (k-1) caras del símplex, y si todos los nodos están anillados, el punto del generador está en el interior del símplex.

El caso especial de politopos uniformes con simetría no reflexiva está representado por un marcado secundario en el que se elimina el punto central de un nodo anillado (llamado "agujero"). Estas formas son alternancias de politopos con simetría reflexiva, lo que implica que los nodos alternativos se eliminan. El politopo resultante tendrá una subsimetría del grupo de Coxeter original. Una alternancia truncada se llama achatada.

Un solo nodo representa un solo espejo. Esto se llama grupo A₁. Si está anillado, esto crea un segmento perpendicular al espejo, representado como {}.
Dos nodos no conectados representan dos espejos perpendiculares. Si ambos nodos están anillados, se puede crear un rectángulo o un cuadrado cuando el punto está a la misma distancia de ambos espejos.
Dos nodos unidos por una rama de orden n pueden crear un n-ágono si el punto está en un espejo y un 2n-ágono si el punto está fuera de ambos espejos. Esto forma el grupo I₁(n).
Dos espejos paralelos pueden representar un grupo de polígonos infinitos I₁(∞), también llamado Ĩ₁.
Tres espejos formando un triángulo generan imágenes como las vistas en un caleidoscopio tradicional y pueden representarse por tres nodos conectados en un triángulo. Los ejemplos repetidos tendrán ramas etiquetadas como (3 3 3), (2 4 4), (2 3 6), aunque las dos últimas se pueden dibujar como una línea (con las ramas 2 omitidas). Estas configuraciones generarán teselados uniformes.
Tres espejos pueden generar poliedros uniformes; incluyendo números racionales se genera el conjunto de los triángulos de Schwarz.
Tres espejos, con uno perpendicular a los otros dos, pueden formar un prisma uniforme.


Hay 7 construcciones uniformes reflexivas dentro de un triángulo general, basadas en 7 posiciones del generador topológico dentro del dominio fundamental. Cada espejo activo genera una arista, con dos espejos activos se tienen generadores en los lados del dominio y con tres espejos activos se tiene el generador en su interior. Se pueden resolver uno o dos grados de libertad para una posición única imponiendo iguales longitudes de arista del poliedro o teselado resultante.	Ejemplo de 7 generadores en la simetría octaedral, triángulo de dominio fundamental (4 3 2), con la octava generación de achatado como alternancia

Los duales de los politopos uniformes a veces están marcados con una barra perpendicular que reemplaza a los nodos anillados y una barra con un orificio para los nodos de los achatados. Por ejemplo, representa un rectángulo (como dos espejos ortogonales activos), y representa su polígono dual, el rombo.

Ejemplo de poliedros y teselados

Por ejemplo, el grupo de Coxeter B₃ tiene un diagrama . Esta configuración también se denomina simetría octaédrica.

Hay 7 poliedros de aristas uniformes convexos que pueden construirse a partir de este grupo de simetría y otros 3 a partir de sus subsimetrías alternantes, cada uno con un diagrama de Coxeter-Dynkin marcado de forma única. El símbolo de Wythoff representa un caso especial del diagrama de Coxeter para gráficos de rango 3, con las 3 órdenes de rama nombradas, en lugar de omitir las ramas de orden 2. El símbolo de Wythoff puede contemplar la forma de "achatado", pero no las alternancias generales sin todos los nodos anillados.

Poliedros octaédricos uniformes
Simetría: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duales a los poliedros uniformes
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Se pueden generar las mismas construcciones en grupos de Coxeter desarticulados (ortogonales) como el prisma uniforme, y se pueden ver más claramente como teselados de diedros y hosoedros en la esfera, como esta familia [6]×[] o [6,2]:

Poliedros esféricos diédricos hexagonales uniformes
Simetría: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duales a los uniformes

V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

En comparación, la familia [6,3], , produce un conjunto paralelo de 7 teselados uniformes del plano euclídeo, y sus duales. De nuevo hay 3 alternancias y alguna versión de semi simetría.

Teselados hexagonales
Simetría: [6,3], (*632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}


6³	3.12²	(3.6)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Uniform duals

V6³	V3.12²	V(3.6)²	V6³	V3⁶	V3.4.6.4	V.4.6.12	V3⁴.6	V3⁶

En el plano hiperbólico [7,3], la familia produce un conjunto paralelo de teselados uniformes y sus duales. Solo hay 1 alternancia (achatado) ya que todos los órdenes de las ramas son impares. Se pueden ver muchas otras familias hiperbólicas de teselados uniformes en teselados uniformes en el plano hiperbólico.

Teselado hiperbólico
Simetría: [7,3], (*732)							[7,3]⁺, (732)


{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
Duales uniformes


V7³	V3.14.14	V3.7.3.7	V6.6.7	V3⁷	V3.4.7.4	V4.6.14	V3.3.3.3.7

Grupos afines de Coxeter

Las familias de teselaciones euclídeas uniformes convexas están definidas por los grupos de Coxeter afines. Estos grupos son idénticos a los grupos finitos con la inclusión de un nodo agregado. Para estos casos, se mantienen las asignaciones de letras, con una virgulilla ("~") por encima de la letra. El índice se refiere al grupo finito, por lo que el rango es el índice más 1. Los símbolos de Witt para los grupos afines figuran a continuación precedidos con la palabra también:

${\tilde {A}}_{n-1}$ : los diagramas de este tipo son ciclos (también P_n)
${\tilde {C}}_{n-1}$ está asociado con la familia de teselaciones regulares hipercúbicas { $4, 3, ...., 4$ } (también R_n)
${\tilde {B}}_{n-1}$ relacionado con C por un espejo eliminado (también S_n)
${\tilde {D}}_{n-1}$ relacionado con C por dos espejos eliminados (también _nX)
${\tilde {E}}_{6}$ , ${\tilde {E}}_{7}$ , ${\tilde {E}}_{8}$ (también T₇, T₈, T₉)
${\tilde {F}}_{4}$ forma la teselación regular {3,4,3,3} (también U₅)
${\tilde {G}}_{2}$ forma los dominios fundamentales triangulares 30-60-90 (también V₃)
${\tilde {I}}_{1}$ son dos espejos paralelos (= ${\tilde {A}}_{1}$ = ${\tilde {C}}_{1}$ ) (también W₂)

Los grupos compuestos también se pueden definir como proyecciones ortogonales. El uso más común de ${\tilde {A}}_{1}$ , como ${\tilde {A}}_{1}^{2}$ , representa dominios cuadrados o rectangulares (tableros de ajedrez) en el plano euclídeo. Y ${\tilde {A}}_{1}{\tilde {G}}_{2}$ representa los dominios fundamentales con forma de prisma triangular en el espacio euclídeo tridimensional.

Gráficos afines de Coxeter entre 2 y 10 nodos
Rango	${\tilde {A}}_{1+}$ (P₂₊)	${\tilde {B}}_{3+}$ (S₄₊)	${\tilde {C}}_{1+}$ (R₂₊)	${\tilde {D}}_{4+}$ (Q₅₊)	${\tilde {E}}_{n}$ (T_n+1) / ${\tilde {F}}_{4}$ (U₅) / ${\tilde {G}}_{2}$ (V₃)
2	${\tilde {A}}_{1}$ =[∞]		${\tilde {C}}_{1}$ =[∞]
3	${\tilde {A}}_{2}$ =[3^[3]] *		${\tilde {C}}_{2}$ =[4,4] *		${\tilde {G}}_{2}$ =[6,3] *
4	${\tilde {A}}_{3}$ =[3^[4]] *	${\tilde {B}}_{3}$ =[4,3^1,1] *	${\tilde {C}}_{3}$ =[4,3,4] *	${\tilde {D}}_{3}$ =[3^1,1,3⁻¹,3^1,1] = ${\tilde {A}}_{3}$
5	${\tilde {A}}_{4}$ =[3^[5]] *	${\tilde {B}}_{4}$ =[4,3,3^1,1] *	${\tilde {C}}_{4}$ =[4,3²,4] *	${\tilde {D}}_{4}$ =[3^1,1,1,1] *	${\tilde {F}}_{4}$ =[3,4,3,3] *
6	${\tilde {A}}_{5}$ =[3^[6]] *	${\tilde {B}}_{5}$ =[4,3²,3^1,1] *	${\tilde {C}}_{5}$ =[4,3³,4] *	${\tilde {D}}_{5}$ =[3^1,1,3,3^1,1] *
7	${\tilde {A}}_{6}$ =[3^[7]] *	${\tilde {B}}_{6}$ =[4,3³,3^1,1]	${\tilde {C}}_{6}$ =[4,3⁴,4]	${\tilde {D}}_{6}$ =[3^1,1,3²,3^1,1]	${\tilde {E}}_{6}$ =[3^2,2,2]
8	${\tilde {A}}_{7}$ =[3^[8]] *	${\tilde {B}}_{7}$ =[4,3⁴,3^1,1] *	${\tilde {C}}_{7}$ =[4,3⁵,4]	${\tilde {D}}_{7}$ =[3^1,1,3³,3^1,1] *	${\tilde {E}}_{7}$ =[3^3,3,1] *
9	${\tilde {A}}_{8}$ =[3^[9]] *	${\tilde {B}}_{8}$ =[4,3⁵,3^1,1]	${\tilde {C}}_{8}$ =[4,3⁶,4]	${\tilde {D}}_{8}$ =[3^1,1,3⁴,3^1,1]	${\tilde {E}}_{8}$ =[3^5,2,1] *
10	${\tilde {A}}_{9}$ =[3^[10]] *	${\tilde {B}}_{9}$ =[4,3⁶,3^1,1]	${\tilde {C}}_{9}$ =[4,3⁷,4]	${\tilde {D}}_{9}$ =[3^1,1,3⁵,3^1,1]
11	...	...	...	...

Grupos hiperbólicos de Coxeter

Hay muchos grupos de Coxeter hiperbólicos infinitos. Los grupos hiperbólicos se clasifican como compactos o no, y los grupos compactos tienen dominios fundamentales delimitados. Los grupos hiperbólicos simples compactos (símplices de Lannér) existen de rango 3 a 5. Los grupos simples compactos (símplices de Koszul) existen hasta el rango 10. Los grupos hipercompactos (politopos de Vinberg) se han explorado pero no se han determinado completamente. En 2006, Allcock demostró que hay infinitos politopos compactos de Vinberg para dimensiones de hasta 6, e infinitos politopos de volumen finito de Vinberg para dimensiones de hasta 19,^[4] por lo que no es posible una enumeración completa. Todos estos dominios reflexivos fundamentales, tanto simples como no simples, a menudo se denominan politopos de Coxeter o, a veces, con menos precisión poliedros de Coxeter.

Grupos hiperbólicos en H²

Artículo principal: Teselados uniformes en el plano hiperbólico

Disco de Poincaré de dominios fundamentales triangulares
Ejemplos de triángulos rectángulos [p,q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Ejemplos de triángulos generales [(p,q,r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

Los grupos triangulares hiperbólicos bidimensionales existen como diagramas de Coxeter de rango 3, definidos por un triángulo (p q r) para:

{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1.

Hay infinitos grupos de Coxeter hiperbólicos triangulares compactos, que incluyen grafos lineales y triangulares. Los gráficos lineales existen para triángulos rectángulos (con r = 2).^[5]

Grupos de Coxeter hiperbólicos compactos

Lineal

Cíclico

∞ [p,q],

:
2(p+q)<pq

...

...

...

∞ [(p,q,r)],

: p+q+r>9

			...

Los grupos de Coxeter paracompactos de rango 3 existen como límites a los compactos.

Grafos lineales	Grafos cíclicos
[p,∞] [∞,∞]	[(p,q,∞)] [(p,∞,∞)] [(∞,∞,∞)]

Grupo triangular aritmético

Los grupos triangulares hiperbólicos que también son grupos aritméticos forman un subconjunto finito. Mediante búsqueda por ordenador, la lista completa fue determinada por "Kisao Takeuchi" en su artículo de 1977 "Grupos de triángulos aritméticos".^[6] Hay 85 en total, 76 compactos y 9 paracompactos.

Triángulos rectángulos (p q 2)	Triángulos generales (p q r)
Grupos compactos: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Triángulos rectángulos paracompactos: (4) , , ,	Triángulos generales: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Triángulos generales paracompactos: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), (2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Polígonos de Coxeter hiperbólicos sobre triángulos

Dominios fundamentales de los grupos cuadriláteros
Dominios con vértices ideales
or [∞,3,∞] [iπぱい/λらむだ₁,3,iπぱい/λらむだ₂] (*3222)	or [((3,∞,3)),∞] [((3,iπぱい/λらむだ₁,3)),iπぱい/λらむだ₂] (*3322)	or [(3,∞)^[2]] [(3,iπぱい/λらむだ₁,3,iπぱい/λらむだ₂)] (*3232)	or [(4,∞)^[2]] [(4,iπぱい/λらむだ₁,4,iπぱい/λらむだ₂)] (*4242)	(*3333)
[iπぱい/λらむだ₁,∞,iπぱい/λらむだ₂] (*∞222)	(*∞∞22)	[(iπぱい/λらむだ₁,∞,iπぱい/λらむだ₂,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Se pueden construir otros caleidoscopios hiperbólicos H² a partir de polígonos de orden superior. Al igual que los grupos triangulares, estos caleidoscopios pueden identificarse mediante una secuencia cíclica de órdenes de intersección de espejos alrededor del dominio fundamental, como (abcd ...), o de manera equivalente en notación orbifold como *abcd... Los diagramas de Coxeter-Dynkin para estas configuraciones poligonales caleidoscópicas se pueden ver como dominios fundamentales degenerados (n-1)-símplex, con un orden cíclico de ramas a, b, c ... y las n*(n-3)/2 ramas restantes se etiquetan como infinito (∞), lo que representa los espejos no intersecantes. El único ejemplo no hiperbólico es la simetría euclídea de cuatro espejos en un teselado cuadrado o rectángular como , [∞, 2, ∞] (orbifold *2222). Otra notación de las ramas para los espejos no intersecantes ideada por Vinberg, representa las ramas infinitas como líneas punteadas o discontinuas, por lo que este diagrama puede mostrarse como , con las cuatro ramas de orden 2 suprimidas alrededor del perímetro.

Por ejemplo, un dominio cuadrilátero (a b c d) tendrá dos ramas de orden infinito que conectan espejos ultra paralelos. El ejemplo hiperbólico más pequeño es , [∞, 3, ∞] o [iπぱい/λらむだ₁, 3, iπぱい/λらむだ₂] (orbifold *3222), donde (λらむだ₁, λらむだ₂) son la distancia entre los espejos ultraparalelos. La expresión alternativa es , con tres ramas de orden 2 omitidas alrededor del perímetro. Del mismo modo (2 3 2 3) (orbifold *3232) puede representarse como y (3 3 3 3), (orbifold *3333) puede representarse como un gráfico completo .

El dominio cuadrilátero más alto (∞ ∞ ∞ ∞) es un cuadrado infinito, representado por un gráfico tetraédrico completo con 4 ramas perimetrales como vértices ideales y dos ramas diagonales como infinito (se muestran como líneas de puntos) para los espejos ultraparalelos: .

Compactos (grupos de símplex de Lannér)

Los grupos hiperbólicos compactos se denominan grupos de Lannér, en relación con Folke Lannér, que los estudió por primera vez en 1950.^[7] Solo existen como gráficos de rango 4 y 5. Coxeter estudió los grupos de Coxeter hiperbólicos lineales en su artículo de 1954 "Panales regulares en el espacio hiperbólico",^[8] que incluía dos soluciones racionales en espacios hiperbólicos de 4 dimensiones: [5/2,5,3,3] = y [5,5/2,5,3] = .

Rangos 4–5

Artículo principal: Panales uniformes en el espacio hiperbólico

El dominio fundamental de cualquiera de los dos grupos bifurcantes, [5,3^1,1] y [5,3,3^1,1], es el doble que el de un grupo lineal correspondiente, [5,3,4] y [5,3,3,4 ] respectivamente. Johnson asigna las letras de cada elemento con el mismo criterio que los símbolos de Witt extendidos^[9]

Grupos de Coxeter hiperbólicos compactos
Dimensión H^d	Rango	Cuenta total	Lineal	Bifurcante	Cíclico
H³	4	9	3: ${\overline {BH}}_{3}$ = [4,3,5]: ${\overline {K}}_{3}$ = [5,3,5]: ${\overline {J}}_{3}$ = [3,5,3]:	${\overline {DH}}_{3}$ = [5,3^1,1]:	${\widehat {AB}}_{3}$ = [(3³,4)]: ${\widehat {AH}}_{3}$ = [(3³,5)]: ${\widehat {BB}}_{3}$ = [(3,4)^[2]]: ${\widehat {BH}}_{3}$ = [(3,4,3,5)]: ${\widehat {HH}}_{3}$ = [(3,5)^[2]]:
H⁴	5	5	3: ${\overline {H}}_{4}$ = [3³,5]: ${\overline {BH}}_{4}$ = [4,3,3,5]: ${\overline {K}}_{4}$ = [5,3,3,5]:	${\overline {DH}}_{4}$ = [5,3,3^1,1]:	${\widehat {AF}}_{4}$ = [(3⁴,4)]:

Paracompacto (grupos de símplex de Koszul)

Los grupos de Coxeter hiperbólicos paracompactos (también llamados no compactos) contienen subgrupos afines y tienen dominios fundamentales simplex asintóticos. El grupo de Coxeter hiperbólico paracompacto más alto es el de rango 10. Estos grupos llevan el nombre del matemático francés Jean-Louis Koszul.^[10] También se denominan grupos cuasi-Lannér, porque extienden los grupos compactos de Lannér. La lista se completó mediante búsqueda con ordenador por M. Chein, y se publicó en 1969.^[11]

De acuerdo con Vinberg, todos menos ocho de estos 72 simplex compactos y paracompactos son aritméticos. Dos de los grupos no aritméticos son compactos: y . Los otros seis grupos no aritméticos son todos paracompactos, con cinco grupos tridimensionales , , , y , y un grupo 5-dimensional .

Símplices ideales

Hay 5 grupos de Coxeter hiperbólicos que expresan símplices ideales, grafos en los que la eliminación de cualquier nodo da como resultado un grupo de Coxeter afín. Por lo tanto, todos los vértices de este símplex ideal están en el infinito.^[12]

Rango	Grupo ideal	Subgrupos afines
3	[(∞,∞,∞)]	[∞]
4	[4^[4]]	[4,4]
4	[3^[3,3]]	[3^[3]]
4	[(3,6)^[2]]	[3,6]
6	[(3,3,4)^[2]]	[4,3,3,4], [3,4,3,3]	,

Rangos 4–10

Artículo principal: Panales uniformes paracompactos

Hay un total de 58 grupos de Coxeter hiperbólicos paracompactos de rango 4 a 10. Los 58 se agrupan a continuación en cinco categorías. Johnson asigna las letras como los "símbolos Witt extendidos", utilizando PQRSTWUV de los símbolos de Witt afines y agregando LMNOXYZ. A estos grupos hiperbólicos se les asigna un sobrelineado, o un sombrero, en los cicloesquemas. La notación de corchetes de Coxeter es una representación linealizada del grupo de Coxeter.

Grupos paracompactos hiperbólicos
Rango	Cuenta total	Grupos
4	23	${\widehat {BR}}_{3}$ = [(3,3,4,4)]: ${\widehat {CR}}_{3}$ = [(3,4³)]: ${\widehat {RR}}_{3}$ = [4^[4]]: ${\widehat {AV}}_{3}$ = [(3³,6)]: ${\widehat {BV}}_{3}$ = [(3,4,3,6)]: ${\widehat {HV}}_{3}$ = [(3,5,3,6)]: ${\widehat {VV}}_{3}$ = [(3,6)^[2]]:	${\overline {P}}_{3}$ = [3,3^[3]]: ${\overline {BP}}_{3}$ = [4,3^[3]]: ${\overline {HP}}_{3}$ = [5,3^[3]]: ${\overline {VP}}_{3}$ = [6,3^[3]]: ${\overline {DV}}_{3}$ = [6,3^1,1]: ${\overline {O}}_{3}$ = [3,4^1,1]: ${\overline {M}}_{3}$ = [4^1,1,1]:	${\overline {R}}_{3}$ = [3,4,4]: ${\overline {N}}_{3}$ = [4³]: ${\overline {V}}_{3}$ = [3,3,6]: ${\overline {BV}}_{3}$ = [4,3,6]: ${\overline {HV}}_{3}$ = [5,3,6]: ${\overline {Y}}_{3}$ = [3,6,3]: ${\overline {Z}}_{3}$ = [6,3,6]:	${\overline {DP}}_{3}$ = [3^[]x[]]: ${\overline {PP}}_{3}$ = [3^[3,3]]:
5	9	${\overline {P}}_{4}$ = [3,3^[4]]: ${\overline {BP}}_{4}$ = [4,3^[4]]: ${\widehat {FR}}_{4}$ = [(3²,4,3,4)]: ${\overline {DP}}_{4}$ = [3^[3]x[]]:	${\overline {N}}_{4}$ = [4,3,((4,2,3))]: ${\overline {O}}_{4}$ = [3,4,3^1,1]: ${\overline {S}}_{4}$ = [4,3^2,1]:	${\overline {R}}_{4}$ = [(3,4)²]:	${\overline {M}}_{4}$ = [4,3^1,1,1]:
6	12	${\overline {P}}_{5}$ = [3,3^[5]]: ${\displaystyle {\widehat {$ = [(3⁵,4)]: ${\widehat {AR}}_{5}$ = [(3,3,4)^[2]]:	${\overline {S}}_{5}$ = [4,3,3^2,1]: ${\overline {O}}_{5}$ = [3,4,3^1,1]: ${\overline {N}}_{5}$ = [3,(3,4)^1,1]:	${\overline {U}}_{5}$ = [3³,4,3]: ${\overline {X}}_{5}$ = [3,3,4,3,3]: ${\overline {R}}_{5}$ = [3,4,3,3,4]:	${\overline {Q}}_{5}$ = [3^2,1,1,1]: ${\overline {M}}_{5}$ = [4,3,3^1,1,1]: ${\overline {L}}_{5}$ = [3^1,1,1,1,1]:
7	3	${\overline {P}}_{6}$ = [3,3^[6]]:	${\overline {Q}}_{6}$ = [3^1,1,3,3^2,1]:	${\overline {S}}_{6}$ = [4,3²,3^2,1]:
8	4	${\overline {P}}_{7}$

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]