Théorème de Ramsey
En mathématiques, et plus particulièrement en combinatoire, le théorème de Ramsey, dû à Frank Ramsey (en 1930), est un théorème fondamental de la théorie de Ramsey. Il affirme que pour tout n, tout graphe complet suffisamment grand dont les arêtes sont colorées contient des sous-graphes complets de taille n d'une seule couleur. En théorie des ensembles, une de ses généralisations, le théorème de Ramsey infini, permet de définir un type particulier de grand cardinal.
Définitions et énoncé
[modifier | modifier le code]La théorie de Ramsey est souvent paraphrasée en affirmant qu'on ne peut pas avoir de désordre complet dans une structure assez grande, ou plutôt qu'une telle structure contient nécessairement des sous-structures ayant un certain ordre. Plus précisément, le théorème de Ramsey fini[1] énonce que si l'on impose un tracé en un nombre fixé de couleurs et une taille fixée (par exemple 100), un « dessin » arbitraire suffisamment grand contiendra nécessairement un réseau de cette taille, donc formé de 100 traits adjacents, tous colorés de la même couleur. Un énoncé plus rigoureux demande un peu de vocabulaire de la théorie des graphes, rappelé ci-dessous.
Un graphe complet d'ordre n est un graphe simple non orienté ayant n sommets et dans lequel toute paire de sommets est reliée par une arête (il y a donc n(n – 1)/2 arêtes). Une coloration (des arêtes) d'un graphe[2] est une application de l'ensemble des arêtes du graphe vers un ensemble de c « couleurs » ; une telle application sera appelée une c-coloration. Un graphe ainsi coloré est monochromatique si chaque arête a pour image la même couleur.
Avec ces définitions, on a :
Théorème de Ramsey (fini)[1] — Pour tout entier c et toute suite d'entiers (n1, n2, … , nc), il existe un entier N tel que pour toute coloration en c couleurs du graphe complet KN d'ordre N, il existe une couleur i et un sous-graphe complet de KN d'ordre ni qui soit monochromatique de couleur i.
Le plus petit entier N ayant cette propriété est noté R(n1, n2, … , nc).
Exemple : calcul de R(3,3) = 6
[modifier | modifier le code]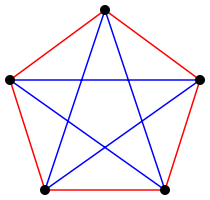
Soit une 2-coloration en rouge et bleu du graphe complet à six sommets K6. Cinq arêtes de ce graphe partent d'un sommet quelconque v, et donc, d'après le principe des tiroirs[3], trois d'entre elles au moins (mettons {v, r}, {v, s} et {v, t}) sont de la même couleur, qu'on peut supposer bleue sans perte de généralité. Si l'une des arêtes {r, s}, {r, t} ou {s, t} est également bleue, le triangle correspondant ({v, r, s} dans le premier cas) est entièrement bleu ; sinon, c'est le triangle formé par ces trois arêtes ({r, s, t}) qui est entièrement rouge. On vient donc de montrer que tout K6 2-coloré contient un K3 monochromatique, et donc que R(3, 3) est inférieur ou égal à 6.
On peut également démontrer ce résultat par double dénombrement (ce qui permet de le généraliser) : on compte le nombre de triplets (ordonnés) de sommets (x, y, z) tels que l'arête {x, y} soit rouge et l'arête {y, z} bleue. Chaque sommet n'appartient à aucun tel triplet si les cinq arêtes partant de ce sommet sont de la même couleur, appartient à 1 × 4 = 4 triplets si quatre arêtes sont d'une même couleur, et à 2 × 3 = 6 triplets si trois arêtes sont d'une des couleurs et deux de l'autre. Il y a donc au plus 6 × 6 = 36 triplets de ce type. Or chaque triangle {x, y, z} non monochromatique contribue pour exactement 2 tels triplets. Il y a donc au plus 18 triangles non monochromatiques, et comme K6 contient triangles, deux d'entre eux au moins sont monochromatiques.
On peut réinterpréter ce résultat sous la forme suivante : dans tout graphe ayant au moins 6 sommets, trois d'entre eux sont connectés deux à deux, ou trois d'entre eux n'ont aucune connexion.
Cette question est fréquemment proposée sous forme d'un problème de mathématiques récréatives[4] ; la version précédente est souvent formulée en termes de « Théorème des amis et des étrangers » car dans une assemblée de six personnes trois d'entre elles se connaissent mutuellement ou trois d'entre elles s'ignorent mutuellement[5].
En revanche, il est possible de 2-colorer K5 sans aucun K3 monochromatique (une telle coloration, unique à isomorphisme près, est montrée à droite), ce qui démontre que R(3, 3) > 5.
Ainsi, R(3, 3) = 6.
Démonstration du théorème de Ramsey
[modifier | modifier le code]Cas de deux couleurs
[modifier | modifier le code]Dans le cas d'une 2-coloration, on va raisonner par récurrence sur r + s. La définition implique clairement que, pour tout n, R(n, 1) = R(1, n) = 1. Montrons que R(r, s) existe en en donnant un majorant explicite. On suppose (hypothèse de récurrence) que R(r − 1, s) et R(r, s − 1) existent. On va montrer (Lemme 1) que R(r, s) ≤ R(r − 1, s) +R(r, s − 1)
Démonstration du lemme. Considérons un graphe complet 2-coloré ayant R(r − 1, s) + R(r, s − 1) sommets. Choisissant un sommet v, on définit une partition des autres sommets en deux ensembles M et N par « w appartient à M si (v, w) est bleue » et « w appartient à N si (v, w) est rouge ». Le graphe ayant R(r − 1, s) + R(r, s − 1) = |M| + |N| + 1 sommets, on a |M| ≥ R(r − 1, s) ou |N| ≥ R(r, s − 1). Dans le premier cas, si M contient un Ks monochromatique rouge, il en est du même du graphe initial ; sinon, M contient un Kr–1 monochromatique bleu, et donc M ∪ {v} contient un Kr bleu par définition de M. Échangeant les couleurs, on a le même résultat (pour N) dans le second cas. Le lemme est donc démontré, ce qui achève par récurrence la démonstration du théorème pour deux couleurs.
Remarque : dans la démonstration précédente, si R(r − 1, s) et R(r, s − 1) sont tous deux pairs, on peut légèrement améliorer l'inégalité du lemme[6], obtenant R(r, s) ≤ R(r − 1, s) + R(r, s − 1) − 1.
Cas général
[modifier | modifier le code]Le cas général se démontre également par récurrence, cette fois sur le nombre c de couleurs. Le résultat est trivial pour c = 1 et vient d'être démontré pour c = 2. Si c > 2, on va montrer l'inégalité suivante (Lemme 2) : R(n1, … , nc) ≤ R(n1, … , nc−2, R(nc−1, nc)).
Démonstration du lemme. Soit une c-coloration du graphe complet Kt ayant t sommets, où t = R(n1, … , nc−2, R(nc−1, nc)). Identifiant les couleurs c − 1 et c, on obtient une (c-1)-coloration du graphe qui, d'après l'hypothèse de récurrence, contient soit un Kni monochromatique de couleur i avec 1 ≤ i ≤ c − 2, soit un KR(nc−1, nc) de la couleur obtenue par identification. Le premier cas satisfait le lemme ; dans le second, on est donc ramené à un problème de 2-coloration et, par définition de R(nc−1, nc), on doit avoir soit un Knc−1 (c − 1)-monochrome, soit un Knc c-monochrome. Dans les deux cas, ceci achève la démonstration du lemme. Par récurrence, le cas général est donc prouvé.
Nombres de Ramsey
[modifier | modifier le code]Les nombres R(r, s), et leurs extensions à un nombre de couleurs quelconque, sont appelés des nombres de Ramsey. Un majorant pour R(r, s) peut être déduit de la démonstration précédente ; d'autres arguments donnent des minorants (le premier fut obtenu par Paul Erdős à l'aide de la méthode probabiliste, qu'il développa à cette occasion).
Cependant, il reste un écart important entre les meilleurs minorants et majorants connus et il n'y a que très peu de couples (r, s) pour lesquels on a pu déterminer la valeur exacte de R(r, s). En général, déterminer un minorant L pour R(r, s) revient à exhiber une 2-coloration du graphe KL−1 ne contenant aucun Kr bleu et aucun Ks rouge ; une telle coloration du graphe Kn est souvent appelée un graphe (r, s, n). Des majorants sont souvent plus difficiles à établir : on doit, soit contrôler toutes les colorations possibles pour vérifier qu'il n'y a pas de contre-exemple, soit découvrir un argument mathématique prouvant qu'il n'y en a pas. Bien que des programmes informatiques sophistiqués évitent d'envisager toutes les 2-colorations possibles (par exemple en utilisant des arguments de symétrie, ou des techniques d'exploration d'arbres), la recherche de contre-exemples, ou la preuve par recherche exhaustive qu'il n'en existe pas, est une tâche que les logiciels existant ne peuvent accomplir que pour des graphes de petite taille : la complexité d'une recherche exhaustive est en effet, pour un graphe de n sommets, de l'ordre de O(2n(n −1)/2) (en utilisant la notation de Landau)[7],[8].
Comme démontré plus haut, R(3, 3) = 6. Il est facile de voir que R(4, 2) = 4 et, plus généralement, que R(s, 2) = s pour tout s (un graphe monochromatique de s − 1 sommets montre que R(s, 2) ≥ s ; un graphe de s sommets non entièrement rouge contient une arête bleue, donc un K2 monochromatique). Utilisant alors le lemme 1 de la démonstration précédente, on voit que R(4, 3) ≤ R(4, 2) + R(3, 3) − 1 = 9, et donc que R(4, 4) ≤ R(4, 3) + R(3, 4) ≤ 18. Parmi les 6,4.1022 2-colorations du graphe complet à 16 sommets (identifiées aux graphes non orientés quelconques à 16 sommets, en convenant qu'on colorie en bleu une arête si elle relie deux sommets du graphe non orienté, et en rouge sinon), il n'y a (à isomorphisme près) que deux graphes (4, 4, 16) (c'est-à-dire des 2-colorations du graphe complet K16 sans aucun K4 monochromatique) et un seul graphe (4, 4, 17) (le graphe de Paley d'ordre 17) parmi les 2,46.1026 2-colorations de K17[9] (ces nombres montrent bien la difficulté d'une recherche exhaustive) ; ce résultat fut démontré par Evans, Pulham et Sheehan en 1979. Il en résulte que R(4, 4) = 18. Enfin[10], R(4, 5) = 25.
On ignore la valeur exacte de R(5, 5), mais on sait depuis 1997 qu'elle est comprise entre 43 et 49[11],[12] (en 2017, cet encadrement a été légèrement amélioré : on sait désormais que R(5,5) est inférieur ou égal à 48[13]) ; il est cependant conjecturé que 43 est la vraie valeur[12]. Erdős a illustré la difficulté d'une détermination exacte en demandant d'imaginer qu'une armée extra-terrestre bien plus puissante que nous débarque et demande la valeur de R(5, 5), faute de quoi ils détruiront notre planète. Dans ce cas, dit-il, nous devrions mobiliser tous nos ordinateurs et tous nos mathématiciens dans l'espoir de déterminer ce nombre. Mais s'ils nous demandaient R(6, 6), nous ferions mieux d'essayer de détruire les extra-terrestres[14].
McKay, Radziszowski et Exoo ont employé des méthodes de construction de graphe assistée par ordinateur pour formuler en 1997 la conjecture selon laquelle R(5, 5) vaut exactement 43. Ils construisirent une liste de 656 graphes de type (5, 5, 42), et arrivèrent à la même liste par plusieurs méthodes distinctes, les amenant à conjecturer que leur liste est complète ; aucun de ces 656 graphes ne peut être étendu à un graphe (5, 5, 43)[12].
Pour R(r, s) avec r, s > 5, on ne connait que des bornes assez lâches. Les minorants pour R(6, 6) et R(8, 8) n'ont d'ailleurs pas été améliorés depuis, respectivement, 1965 et 1972[15].
La table suivante[15] donne R(r, s) pour les valeurs de r et s jusqu'à 10 (avec r ≤ s, la table étant symétrique puisque R(r, s) = R(s, r)). Lorsque la valeur exacte n'a pas été déterminée, la table donne le meilleur encadrement connu.
| r,s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||
| 2 | 1 | 2 | ||||||||
| 3 | 1 | 3 | 6 | |||||||
| 4 | 1 | 4 | 9 | 18 | ||||||
| 5 | 1 | 5 | 14 | 25 | 43–48 | |||||
| 6 | 1 | 6 | 18 | 36–41 | 58–87 | 102–165 | ||||
| 7 | 1 | 7 | 23 | 49–61 | 80–143 | 113–298 | 205–540 | |||
| 8 | 1 | 8 | 28 | 58–84 | 101–216 | 132–495 | 217–1031 | 282–1870 | ||
| 9 | 1 | 9 | 36 | 73–115 | 126–316 | 169–780 | 241–1713 | 317–3583 | 565–6588 | |
| 10 | 1 | 10 | 40–42 | 92–149 | 144–442 | 179–1171 | 289–2826 | 331–6090 | 581–12677 | 798–23556 |
Comportement asymptotique
[modifier | modifier le code]L'inégalité R(r, s) ≤ R(r − 1, s) + R(r, s − 1) implique par récurrence que
Ce résultat, dû à Paul Erdős et George Szekeres, donne en particulier, lorsque r = s, que
Un minorant exponentiel,
fut obtenu par Erdős en 1947[16] et joua un rôle essentiel dans son introduction de la méthode probabiliste en combinatoire. L'écart entre ces deux bornes est important : pour s = 10, par exemple, on en déduit que 101 ≤ R(10, 10) ≤ 48 620. Cependant, l'ordre de croissance exponentielle n'a pu être amélioré depuis cette époque (on a seulement des résultats équivalents à ) ; de plus, on ne connait pas de construction explicite de graphes (n, n, L) (justifant le minorant L) pour lesquels L serait une fonction exponentielle de n. Les meilleures bornes actuellement connues de ces nombres de Ramsey diagonaux sont[17],[18] :
On a pu établir que les nombres de Ramsey R(3, t) sont d'ordre ; ce résultat est équivalent à dire que le plus petit stable dans un graphe sans triangle à n sommets est d'ordre . Plus généralement, pour R(s, t) avec s fixé et t tendant vers l'infini, les meilleures bornes connues sont[19] :
Un exemple à trois couleurs : R(3,3,3) = 17
[modifier | modifier le code]
R(3, 3, 3) est le seul nombre de Ramsey (non trivial) correspondant à plus de deux couleurs dont on connait la valeur exacte : R(3, 3, 3) = 17.
- Démonstration
- Partons d'une 3-coloration (en rouge, vert et jaune) d'un graphe complet Kn ne contenant pas de triangle monochromatique, et fixons un sommet v ; le voisinage vert de v, noté V, est le sous-graphe de Kn dont les sommets sont les u tels que l'arête {u,v} soit verte. V ne peut contenir d'arête verte (sinon un triangle vert serait formé de cette arête et des deux arêtes la reliant à v). V est donc 2-coloré en rouge et jaune, et ne contient pas de triangle monochromatique ; comme R(3, 3) = 6, V a au plus 5 sommets. Raisonnant de même sur les voisinages rouges et jaunes de v, on voit qu'ils contiennent également 5 sommets au plus, et donc en définitive que le graphe complet peut avoir au plus 1 + 5 + 5 + 5 = 16 sommets ; ainsi, R(3, 3, 3) ≤ 17.
- Pour montrer que R(3, 3, 3) ≥ 17, il suffit d'exhiber une 3-coloration de K16 ne contenant pas de triangles monochromatiques. À isomorphisme près, il en existe exactement 2, représentés à droite (dans ces tracés, les sommets numérotés v11 à v15 ont été dupliqués à droite et à gauche pour faciliter la lisibilité).
- En définitive, R(3, 3, 3) = 17.
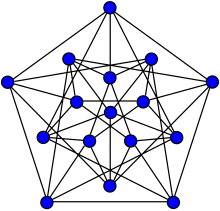
Dans les deux 3-colorations précédentes, les trois sous-graphes formés des arêtes d'une seule couleur sont isomorphes au graphe de Clebsch.
Généralisations du théorème
[modifier | modifier le code]Paul Erdős et Leo Moser définissent des nombres analogues (encore appelés nombres de Ramsey) pour des graphes orientés[20]. Ils démontrent pour tout n l'existence d'un entier Q tel que tout graphe complet orienté (encore appelé un tournoi) ayant Q sommets contienne un sous-graphe acyclique à n sommets, et notent R(n) le plus petit de ces entiers (l'analogie avec R(n, n ; 2) consiste à considérer chaque direction comme une couleur ; un graphe acyclique est alors un graphe dans lequel les arêtes ont toutes « la même direction », donc un graphe monochromatique). On obtient R(1) = 1, R(2) = 2, R(3) = 4, R(4) = 8, R(5) = 14, R(6) = 28, 32 ≤ R(7) ≤ 55 ; la détermination exacte de R(8) est un autre problème que, comme Erdős pour R(5, 5), on n'aimerait pas voir posé par de puissants extra-terrestres.
Le théorème de Ramsey s'étend également aux hypergraphes. Un m-hypergraphe est une généralisation des graphes consistant à appeler « arêtes » des ensembles de m sommets – les graphes ordinaires sont donc des 2-hypergraphes. Le résultat de Ramsey est que pour tout m et c, et toute suite n1, … , nc, il existe un entier R(n1, … , nc ; c, m) tel que pour toute c-coloration d'un m-hypergraphe complet d'ordre R(n1, … , nc ; c, m), il existe un i et un sous-hypergraphe complet d'ordre ni monochromatique de couleur i. La démonstration se fait par récurrence sur m, en partant du cas m = 2 des graphes ordinaires.
Enfin, de nombreuses variantes du théorème sont obtenues en exigeant des conditions supplémentaires sur les sous-graphes monochromatiques dont il garantit l'existence, ou en remplaçant les graphes complets par d'autres structures ; cet ensemble de résultats constitue la théorie de Ramsey. Ainsi, le théorème de van der Waerden (dont le théorème de Szemerédi est une généralisation) est obtenu en remplaçant « graphe complet » par « progression arithmétique » ; un autre exemple célèbre est, en identifiant les sommets du graphe K2n à ceux d'un hypercube, la démonstration que, pour toute 2-coloration, il existe un sous-graphe K4 monochromatique dont les quatre sommets sont coplanaires, si n est supérieur au nombre de Graham[21].
Le théorème de Ramsey infini
[modifier | modifier le code]Un résultat analogue, encore appelé théorème de Ramsey (ou théorème de Ramsey infini lorsque le contexte n'est pas clair), s'applique aux graphes infinis. Les représentations graphiques étant moins parlantes dans ce cas, les résultats de ce type sont généralement formulés dans le langage de la théorie des ensembles. On note ici E(n) (pour tout ensemble E et tout entier n) l'ensemble des parties de E de taille n et, en appelant « coloration finie » d'un ensemble une partition finie de cet ensemble, une partie est dite « monochrome » si elle est incluse dans l'une des classes de la partition (appelées « couleurs »).
Théorème de Ramsey infini — Soit X un ensemble infini dénombrable. Pour toute coloration finie de X(n), il existe un sous-ensemble infini M de X tel que M(n) soit monochrome.
- Démonstration
- Soit c le nombre de couleurs. On raisonne par récurrence sur n. Si n = 1, l'énoncé est vrai car dans toute partition finie d'un ensemble infini, l'un des sous-ensembles est infini. Supposons le théorème vrai pour n ≤ r, et montrons-le pour n = r + 1. Étant donné une c-coloration P de X(r+1), soit a0 un élément de X et Y = X\{a0}. P induit une c-coloration P' de Y(r) définie par : la P'-couleur d'une partie s de Y est la P-couleur de s∪{a0}. D'après l'hypothèse de récurrence, il existe un sous-ensemble infini Y1 de Y tel que Y1(r) soit monochrome. Il y a donc un élément a0 et un ensemble infini Y1 tels que tous les sous-ensembles à r + 1 éléments de X formés de a0 et de r éléments de Y1 ont la même couleur. Le même argument montre qu'il y a un élément a1 de Y1 et un sous-ensemble infini Y2 de Y1 avec la même propriété, et donc, par récurrence, on obtient une suite infinie (a0, a1, a2, …) telle que la couleur de n'importe quel sous-ensemble à r + 1 éléments de la forme (ai(1), ai(2), … , ai(r + 1)) avec i(1) < i(2) < … < i(r + 1) dépend seulement de i(1). Il y a de plus un nombre infini de valeurs i(n) pour lesquelles cette couleur sera la même. L'ensemble de ces ai(n) est par construction un ensemble ayant la propriété cherchée.
Ce théorème est à l'origine de la notion de cardinal de Ramsey (qu'on démontre être nécessairement un grand cardinal). Soit
Le cas infini implique le cas fini
[modifier | modifier le code]On peut déduire le théorème fini de la version infinie en raisonnant par l'absurde, ou plutôt par contraposition. Supposons que le théorème fini soit faux. Il existe des entiers c, n, T tels que pour tout entier k, il existe une c-coloration de {1, 2, … , k}(n) sans ensemble monochromatique de cardinal T. Soit Ck l'ensemble de ces c-colorations.
Pour tout k, la restriction d'une coloration de Ck+1 à {1, 2, … , k}(n) obtenue en ignorant les ensembles contenant k + 1 est une coloration de Ck. Définissant C1k comme l'ensemble des colorations de Ck qui sont des restrictions de colorations dans Ck+1, on voit que C1k n'est pas vide, puisque Ck+1 ne l'est pas.
De même, la restriction d'une coloration dans C1k+1 est dans C1k, ce qui permet de définir C2k comme l'ensemble non vide de ces restrictions ; par récurrence, on peut donc définir Cmk pour tous les entiers m et k.
On a donc pour tout k la suite décroissante , et tous les ensembles de cette suite sont non vides. De plus, Ck est fini (de cardinal inférieur ou égal à ). Il en résulte que la suite est stationnaire, et que est non vide. Ainsi, toute coloration de Dk est la restriction d'une coloration dans D1k+1. Remontant alors en prolongeant une coloration de Dk à Dk+1, puis à Dk+2, et ainsi de suite, on construit une coloration de sans aucun ensemble monochromatique de cardinal T. Ceci est la contradiction cherchée avec le théorème de Ramsey infini ; par contraposition, ce dernier entraîne le cas fini.
D'un point de vue topologique, ce raisonnement peut s'interpréter comme un argument de compacité[22].
Historique et applications
[modifier | modifier le code]Frank Ramsey a publié ce théorème dans l'article On a problem of formal logic (Ramsey 1930). L'article en question est un article de logique mathématique et le théorème était au départ une étape du raisonnement. Le résultat a été popularisé par Paul Erdős, notamment dans l'article A combinatorial problem in geometry (Erdős et Szekeres 1935)[23].
Le théorème de Ramsey est utilisé entre autres en informatique théorique, par exemple pour montrer des bornes sur l'efficacité des structures de données[24].
Notes et références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Ramsey's theorem » (voir la liste des auteurs).
- Ramsey (1930) a démontré ce résultat sous une forme légèrement différente, correspondant à une application à un problème de logique formelle.
- Le sens donné ici à cette expression est différent de celui de l'article Coloration des arêtes d'un graphe, qui réclame de plus que deux arêtes adjacentes soient de couleurs distinctes.
- Dont on peut voir la théorie de Ramsey comme une vaste généralisation.
- C'était par exemple un des énoncés de la Putnam Competition de 1953. On le trouve également dans (en) Eugene P. Northrop, Riddles in mathematics [« Fantaisies et paradoxes mathématiques »], .
- Jean-Paul Delahaye, chronique "Logique & Calcul", Pour la Science, septembre 2017, Cinq énigmes pour la rentrée, paragraphe "Enigme 3 : se connaître ou s'ignorer", pages 82 et 83.
- (en) « Party Acquaintances ».
- (en) 2.6 Ramsey Theory from Mathematics Illuminated.
- Plus précisément, Kn possède n(n–1)/2 arêtes ; il y a donc à isomorphisme près (par permutation des sommets) un nombre de 2-colorations au moins égal à n(n–1)/2n! (parce qu'une permutation des sommets peut ne pas changer la coloration), mais montrer que deux graphes sont isomorphes est un problème NP-complet, c'est pourquoi l'on ne peut guère améliorer l'estimation donnée pour une approche exhaustive.
- (en) B. McKay, « Ramsey Graphs ».
- (en) Brendan D. McKay et Stanislaw P. Radziszowski (en), « R(4, 5) = 25 », Journal of Graph Theory, (DOI 10.1002/jgt.3190190304).
- (en) G. Exoo, « A lower bound for R(5, 5) », Journal of Graph Theory, vol. 13, , p. 97-98 (DOI 10.1002/jgt.3190130113).
- (en) Brendan D. McKay et Stanislaw P. Radziszowski, « Subgraph counting identities and Ramsey numbers », Journal of Combinatorial Theory, (lire en ligne).
- (en) Vigleik Angeltveit et Brendan McKay, « », .
- (en) Joel H. Spencer, Ten Lectures on the Probabilistic Method : Second Edition, SIAM, , 88 p. (ISBN 978-0-89871-325-1, lire en ligne), p. 4.
- Pour plus de données, accompagnées de références, voir (en) Stanisław Radziszowski, « Small Ramsey numbers », Dynamic Surveys, vol. DS1, (lire en ligne).
- (en) Paul Erdős, « Some remarks on the theory of graphs », Bull. Amer. Math. Soc., vol. 53, no 4, , p. 292-294 (DOI 10.1090/S0002-9904-1947-08785-1, lire en ligne).
- (en) J. Spencer, « Ramsey's theorem – a new lower bound », J. Combin. Theory Ser. A, vol. 18, , p. 108-115 (DOI 10.1016/0097-3165(75)90071-0).
- (en) D. Conlon, « A new upper bound for diagonal Ramsey numbers », Annals of Mathematics, vol. 170, no 2, , p. 941-960 (DOI 10.4007/annals.2009.170.941).
- Dues respectivement à (en) Tom Bohman et Peter Keevash, « The early evolution of the H-free process », Invent. Math., vol. 181, no 2, , p. 291-336 (DOI 10.1007/s00222-010-0247-x) et à (en) Miklós Ajtai, János Komlós et Endre Szemerédi, « A note on Ramsey numbers », J. Combin. Theory Ser. A, vol. 29, no 3, , p. 354-360 (DOI 10.1016/0097-3165(80)90030-8).
- (en) P. Erdős et L. Moser, « On the representation of directed graphs as unions of orderings », Magyar Tud. Akad. Mat. Kutató Int. Közl., vol. 9, , p. 125-132 (MR 0168494, lire en ligne).
- Pour plus de détails, voir (en) John Baez, « A while back I told you about Graham's number... », .
- Thomas Budsinski, « Théorie de Ramsey », sur ENS Lyon, (consulté le ), p. 6.
- Pour cette partie historique, voir le sous-chapitre 1.7 de Graham, Rothschild et Spencer 1990, p. 19.
- Voir par exemple : Andrew Chi-Chih Yao, « Should Tables Be Sorted? », Journal of the ACM, vol. 28, no 3, , p. 615-628.
Bibliographie
[modifier | modifier le code]- (en) Paul Erdős et George Szekeres, « A combinatorial problem in geometry », Compositio Mathematica, vol. 2, , p. 463-470 (DOI 10.1007/978-0-8176-4842-8_3, lire en ligne).
- (en) Ronald L. Graham, Bruce Lee Rothschild et Joel H. Spencer, Ramsey Theory, Wiley-Interscience, , 2e éd. (1re éd. 1980)
- (en) F. P. Ramsey, « On a problem of formal logic », Proc. London Math. Soc., vol. 30, , p. 264-286 (lire en ligne).
- Martin Aigner et Günter M. Ziegler, chap. 32 « Les probabilités facilitent (parfois) le dénombrement », dans Raisonnements divins, Springer, (ISBN 9782287597237, lire en ligne), p. 229-234`.
- Claude Berge, Graphes et Hypergraphes, Paris, Dunod, (ISBN 978-2-04-009755-4).
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]- Coloration de graphe
- Théorème des amis et des étrangers
- Graphe d'amitié
- Théorème de Paris-Harrington
Liens externes
[modifier | modifier le code]- (en) « Ramsey theorem », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
- (en) Eric W. Weisstein, « Ramsey Number », sur MathWorld (bornes pour tous les nombres de Ramsey jusqu'à R(19,19))
- (en) Ramsey Numbers – Geoffrey Exoo (Le contre-exemple montrant que R(5,5) > 42)
- (en) Norman Do, « Party problems and Ramsey theory », Austr. Math. Soc. Gazette, vol. 33, no 5, , p. 306-312 (lire en ligne)
- (en) Zhengbing Bian, Fabian Chudak, William G. Macready, Lane Clark et Frank Gaitan, « Experimental determination of Ramsey numbers », Physical Review Letters, vol. 111, , p. 130505-1 - 130505-6 (DOI 10.1103/PhysRevLett.111.130505, arXiv 1201.1842)














