Rhomboèdre

Rhomboèdre
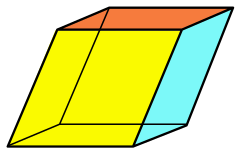
Type	Prisme
Faces	6 losanges
Arêtes	12
Sommets	8
Groupe de symétrie	Ci
Propriétés	convexe, zonoèdre

Pour un rhomboèdre, on a $a=b=c$.

En géométrie, un rhomboèdre est un polyèdre équivalent au cube dont les faces sont des losanges. C'est le cas particulier du parallélépipède obtenu lorsque les arêtes sont de même longueur ; autrement dit, c'est un parallélépipède rhombique.

Dans le cas général, le rhomboèdre peut avoir trois types de faces rhombiques par couple de faces opposées isométriques, caractérisés par les trois angles $\alpha ,\beta ,\gamma$ des faces se rejoignant en un des sommets (voir figure).

Son volume s'obtient par la formule : $a^{3}{\sqrt {1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}$, où $a$ est la longueur commune des arêtes.

Lorsque de plus $\alpha =\beta =\gamma$, autrement dit si toutes les faces sont isométriques, on obtient un trapézoèdre trigonal.

Un rhomboèdre rectangle ($\alpha =\beta =\gamma =90^{\circ }$) est un cube.

Ces propriétés sont importantes en cristallographie, et permettent notamment d'expliquer la parenté entre les systèmes cristallins trigonal, hexagonal et cubique.

Un autre cas particulier est le suivant : il existe un plan de symétrie passant par quatre sommets (avec le groupe de symétrie C_2h), et un cas spécial où il existe un autre plan de symétrie passant par les quatre autres sommets (avec le groupe de symétrie D_2h). Un polyèdre combinant ces deux propriétés est un cube.

Voir aussi

Articles connexes

• Trapézoèdre trigonal
• Forme cristalline
• Système cristallin
• Géométrie dans l'espace