משוואה ממעלה שישית – הבדלי גרסאות

תוכן שנמחק תוכן שנוסף

בשורה

גרסה אחרונה מ־20:31, 26 בדצמבר 2023

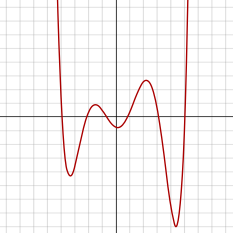
משוואה ממעלה שישית היא משוואה מהצורה $ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0$ , כאשר $a\neq 0$ והמקדמים $a,b,c,d,e,f,g$ יכולים להיות מספרים שלמים, מספרים רציונליים, מספרים ממשיים, מספרי מרוכבים או, באופן כללי יותר, איברים של כל שדה.

פונקציה ממעלה שישית היא פונקציה המוגדרת על ידי פולינום ממעלה שישית. משום שיש להן מעלה זוגית, היא דומה מבחינה גרפית לפונקציה ממעלה רביעית. עם זאת, לפונקציה ממעלה שישית עשויים להיות נקודות קיצון מקומיות נוספות. נגזרת של פונקציה ממעלה שישית היא פונקציה ממעלה חמישית.

מאחר שפונקציה ממעלה שישית על ידי פולינום ממעלה זוגית, יש לה את אותו הגבול כאשר הארגומנט הולך לאינסוף חיובי או שלילי. אם המקדם המוביל $a$ הוא חיובי, אז הפונקציה עולה לפלוס אינסוף משני הצדדים ולכן לפונקציה יש מינימום גלובלי. כמו כן, אם $a$ שלילי, הפונקציה יורדת עד מינוס אינסוף משני הצדדים ולכן יש לה מקסימום גלובלי.

פתרון[עריכת קוד מקור | עריכה]

כמה משוואות ממעלה שישית, כמו $ax^{6}+dx^{3}+g=0$ ניתנות לפתרון באמצעות רדיקלים, אבל משוואות אחרות לא ניתנות לפתרון. בשנת 1824 הוכיח נילס הנריק אבל כי אין פתרון כללי באמצעות רדיקלים למשוואה ממעלה חמישית ומעלה. שנים ספורות לאחר מכן מצא אווריסט גלואה אפיון מלא של כל המשוואות הפולינומיות שניתנות לפתרון באמצעות רדיקלים: אלו המשוואות שחבורת גלואה המתאימה להן היא חבורה פתירה. מחקרים אלו הולידו את תורת גלואה ואת תורת החבורות. גלואה פיתח טכניקות לקביעה האם משוואה נתונה ניתנת לפתרון על ידי רדיקלים^[1]. מתורת גלואה נובע כי משוואה ממעלה שישית ניתנת לפתרון במונחים של רדיקלים, אם ורק אם חבורת הגלואה שלה נמצאת בחבורה מסדר 48, המייצבת חלוקה של קבוצת השורשים לשלוש תת-קבוצות של שני שורשים, או חבורה מסדר 72 המייצבת חלוקה של מערכת השורשים לשתי תת-קבוצות של שלושה שורשים. קיימות נוסחאות כדי לבדוק כל מקרה, ולחשב את השורשים, במקרים שהמשוואה ניתנת לפתרון^[2]. ב-1867 (בעקבות עבודתו של הרמיט על משוואה ממעלה חמישית), הראה Joubert שכל הרחבת שדות ספרבילית מממד 6, במאפיין שאינו 2, נוצרת על ידי איבר המקיים משוואה מהצורה $x^{6}+bx^{4}+cx^{2}+d(x+1)$ ^[3].

משוואה כללית ממעלה שישית ניתנת לפתרון במונחים של פונקציות קמפה דה פרייט. ישנן משוואות ממעלה שישית הניתנות לפתרון על ידי פונקציה היפרגאומטרית כללית במשתנה אחד, באמצעות הגישה של פליקס קליין לפתרון משוואה ממעלה חמישית.

דוגמאות[עריכת קוד מקור | עריכה]

עקומת וואט, שנחקרה בעבודה הראשונית על מנוע הקיטור, היא משוואה ממעלה שישית עם שני משתנים.

אחת השיטות לפתרון משוואה מעוקבת כוללת שינוי במשתנים כדי להשיג משוואה ממעלה שישית, שמשתניה ממעלות 6, 3 ו-0 בלבד. בדרך זו, ניתן לפתור אותה כמו משוואה ריבועית.

ראו גם[עריכת קוד מקור | עריכה]

פונקציה מעוקבת

הערות שוליים[עריכת קוד מקור | עריכה]

^ אריק ווייסטיין, Sextic Equation, באתר MathWorld (באנגלית)
^ T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757
^ H. Kraft / Journal of Algebra 297 (2006) 234–253

[1] אריק ווייסטיין, Sextic Equation, באתר MathWorld (באנגלית)

[2] T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757

[3] H. Kraft / Journal of Algebra 297 (2006) 234–253

[1]

[2]

[3]

@@ שורה 1: / שורה 1: @@
-[[קובץ:Sextic_Graph.svg|שמאל|ממוזער|233x233 פיקסלים| גרף של פונקציה ממעלה שישית, עם 6 [[שורש (של פונקציה)|שורשים]] [[שדה המספרים הממשיים|אמיתיים]] (חותכים את ציר x) ו-5 נקודות קריטיות.]]
+[[קובץ:Sextic_Graph.svg|שמאל|ממוזער|233x233 פיקסלים| גרף של פונקציה ממעלה שישית, עם 6 [[שורש (של פונקציה)|שורשים]] [[שדה המספרים הממשיים|ממשיים]] (חותכים את ציר x) ו-5 נקודות קריטיות.]]
-'''משוואה ממעלה שישית''' היא משוואה מהצורה <math>ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0</math>, כאשר <math>a \neq 0</math> והמקדמים <math>a, b, c, d, e, f, g</math> יכולים להיות [[מספר שלם|מספרים שלמים]], [[מספר רציונלי|מספרים רציונליים]], [[שדה המספרים הממשיים|מספרים ממשיים]], [[מספר מרוכב|מספרי מרוכבים]] או, באופן כללי יותר, אברים של כל [[שדה (מבנה אלגברי)|שדה]].
+'''משוואה ממעלה שישית''' היא משוואה מהצורה <math>ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0</math>, כאשר <math>a \neq 0</math> והמקדמים <math>a, b, c, d, e, f, g</math> יכולים להיות [[מספר שלם|מספרים שלמים]], [[מספר רציונלי|מספרים רציונליים]], [[שדה המספרים הממשיים|מספרים ממשיים]], [[מספר מרוכב|מספרי מרוכבים]] או, באופן כללי יותר, איברים של כל [[שדה (מבנה אלגברי)|שדה]].
-פונקציה ממעלה שישית היא [[פונקציה]] המוגדרת על ידי פולינום ממעלה שישית. משום שיש להן מעלה זוגית, היא דומה מבחינה [[גרף של פונקציה|גרפית]] לפונקציה ממעלה רביעית. עם זאת, לפונקציה ממעלה שישית עשויים להיות [[נקודת קיצון|נקודות קיצון מקומיות]] נוספות. [[נגזרת]] של פונקציה ממעלה שישית היא [[משוואה ממעלה חמישית|פונקציה ממעלה חמישית]].
+פונקציה ממעלה שישית היא [[פונקציה]] המוגדרת על ידי [[פולינום]] ממעלה שישית. משום שיש להן מעלה זוגית, היא דומה מבחינה [[גרף של פונקציה|גרפית]] לפונקציה ממעלה רביעית. עם זאת, לפונקציה ממעלה שישית עשויים להיות [[נקודת קיצון|נקודות קיצון מקומיות]] נוספות. [[נגזרת]] של פונקציה ממעלה שישית היא [[משוואה ממעלה חמישית|פונקציה ממעלה חמישית]].
 מאחר שפונקציה ממעלה שישית על ידי פולינום ממעלה זוגית, יש לה את אותו ה[[גבול (מתמטיקה)|גבול]] כאשר הארגומנט הולך ל[[אינסוף]] חיובי או שלילי. אם [[מקדם (מתמטיקה)|המקדם המוביל]] <math>a</math> הוא חיובי, אז הפונקציה עולה לפלוס אינסוף משני הצדדים ולכן לפונקציה יש מינימום גלובלי. כמו כן, אם <math>a</math> שלילי, הפונקציה יורדת עד מינוס אינסוף משני הצדדים ולכן יש לה מקסימום גלובלי.
 == פתרון ==
-כמה משוואות ממעלה שישית, כמו <math>ax^6 + dx^3 + g = 0</math> ניתנות ל[[פתרון באמצעות רדיקלים]], אבל משוואות אחרות לא ניתנות לפתרון. בשנת [[1824]] הוכיח [[נילס הנריק אבל]] כי אין פתרון כללי באמצעות רדיקלים למשוואה ממעלה חמישית ומעלה. שנים ספורות לאחר מכן מצא [[אווריסט גלואה]] אפיון מלא של כל המשוואות הפולינומיות שניתנות לפתרון באמצעות רדיקלים: אלו המשוואות ש[[חבורת גלואה]] המתאימה להן היא [[חבורה פתירה]]. מחקרים אלו הולידו את [[תורת גלואה]] ואת [[תורת החבורות]]. גלואה פיתח טכניקות לקביעה האם משוואה נתונה ניתנת לפתרון על ידי רדיקלים{{הערה|{{קישור כללי|הכותב=אריק ווייסטיין|כותרת=Sextic Equation|כתובת=http://mathworld.wolfram.com/SexticEquation.html|מידע נוסף=באתר [[MathWorld]]|שפה=אנגלית}}}}. מתורת גלואה נובע כי משוואה ממעלה שישית ניתנת לפתרון במונחים של רדיקלים, [[אם ורק אם]] חבורת הגלואה שלה נמצאת בחבורה מסדר 48, [[פעולת חבורה|המייצבת]] חלוקה של קבוצת השורשים לשלוש תת-קבוצות של שני שורשים, או חבורה מסדר 72 המייצבת חלוקה של מערכת השורשים לשתי תת-קבוצות של שלושה שורשים. קיימות נוסחאות כדי לבדוק כל מקרה, ולחשב את השורשים, במקרים שהמשוואה ניתנת לפתרון{{הערה|T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757|כיוון=שמאל}}. ב-[[1867]] (בעקבות עבודתו של הרמיט על [[המשוואה ממעלה חמישית|משוואה ממעלה חמישית]]), הראה Joubert שכל הרחבת שדות ספרבילית מממד 6, במאפיין שאינו 2, נוצרת על ידי איבר המקיים משוואה מהצורה <math> x^6+bx^4+cx^2+d(x+1)</math> {{מקור=H. Kraft / Journal of Algebra 297 (2006) 234–253}}.
+כמה משוואות ממעלה שישית, כמו <math>ax^6 + dx^3 + g = 0</math> ניתנות ל[[פתרון באמצעות רדיקלים]], אבל משוואות אחרות לא ניתנות לפתרון. בשנת [[1824]] הוכיח [[נילס הנריק אבל]] כי אין פתרון כללי באמצעות רדיקלים למשוואה ממעלה חמישית ומעלה. שנים ספורות לאחר מכן מצא [[אווריסט גלואה]] אפיון מלא של כל המשוואות הפולינומיות שניתנות לפתרון באמצעות רדיקלים: אלו המשוואות ש[[חבורת גלואה]] המתאימה להן היא [[חבורה פתירה]]. מחקרים אלו הולידו את [[תורת גלואה]] ואת [[תורת החבורות]]. גלואה פיתח טכניקות לקביעה האם משוואה נתונה ניתנת לפתרון על ידי רדיקלים{{הערה|{{קישור כללי|הכותב=אריק ווייסטיין|כותרת=Sextic Equation|כתובת=http://mathworld.wolfram.com/SexticEquation.html|מידע נוסף=באתר [[MathWorld]]|שפה=אנגלית}}}}. מתורת גלואה נובע כי משוואה ממעלה שישית ניתנת לפתרון במונחים של רדיקלים, [[אם ורק אם]] חבורת הגלואה שלה נמצאת בחבורה מסדר 48, [[פעולת חבורה|המייצבת]] חלוקה של קבוצת השורשים לשלוש תת-קבוצות של שני שורשים, או חבורה מסדר 72 המייצבת חלוקה של מערכת השורשים לשתי תת-קבוצות של שלושה שורשים. קיימות נוסחאות כדי לבדוק כל מקרה, ולחשב את השורשים, במקרים שהמשוואה ניתנת לפתרון{{הערה|T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757|כיוון=שמאל}}. ב-[[1867]] (בעקבות עבודתו של הרמיט על [[משוואה ממעלה חמישית]]), הראה Joubert שכל [[הרחבת שדות]] ספרבילית מממד 6, במאפיין שאינו 2, נוצרת על ידי איבר המקיים משוואה מהצורה <math> x^6+bx^4+cx^2+d(x+1)</math>{{הערה|H. Kraft / Journal of Algebra 297 (2006) 234–253}}.
 משוואה כללית ממעלה שישית ניתנת לפתרון במונחים של פונקציות קמפה דה פרייט. ישנן משוואות ממעלה שישית הניתנות לפתרון על ידי [[פונקציה היפרגאומטרית]] כללית במשתנה אחד, באמצעות הגישה של [[פליקס קליין]] לפתרון [[משוואה ממעלה חמישית]].
@@ שורה 21: / שורה 21: @@
 == הערות שוליים ==
 {{הערות שוליים}}
+{{משוואות פולינומיות}}
 [[קטגוריה:פולינומים]]

פולינום
משוואות פולינומיות לפי מעלה	משוואה ליניארית (1) • משוואה ממעלה שנייה (2) • משוואה ממעלה שלישית (3) • משוואה ממעלה רביעית (4) • משוואה ממעלה חמישית (5) • משוואה ממעלה שישית (6) • משוואה ממעלה שביעית (7)
פונקציות פולינומיות לפי מעלה	פונקציה ממעלה שלישית
אישים הקשורים במציאת פתרונות או הוכחת אי פתירות	לודוביקו פרארי • מוחמד אבן מוסא אל-ח'ואריזמי • אברהם בר חייא • שיפיונה דל פרו • ניקולו טרטליה • ג'ירולמו קרדאנו • נילס הנריק אבל • אווריסט גלואה • פאולו רופיני • פליקס קליין • ולדימיר ארנולד
כללי	היסטוריה של פתרון משוואות פולינומיות • משפט אבל-רופיני • תורת גלואה • הבעיה השלוש-עשרה של הילברט • פתרון באמצעות רדיקלים • רדיקל ברינג • i (מספר)