मुक्त ज्ञानकोश विकिपीडिया से
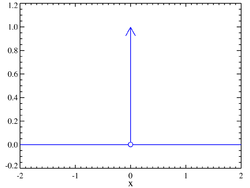
डिरैक डेल्टा फलन का योजनामूलक निरुपण : तीरयुक्त रेखा डिरैक डेल्टा फलन (Dirac delta function) या डिरैक का डेल्टा फलन या δ でるた शून्य होता है तथा सम्पूर्ण वास्तविक रेखा पर इसका समाकल १ होता है। कभी-कभी डेल्टा फलन को मूलबिन्दु पर अनन्त ऊँची किन्तु अत्यन्त पतली स्पाइक के रूप में भी समझा जाता है जिसका कुल क्षेत्रफल १ है। इसे आवेग फलन (इम्पल्स फंक्शन) भी कहते हैं।
इसका उपयोग आदर्श द्रव्यमान के घनत्व या आदर्श आवेश के घनत्व को निरुपित करने के लिये किया जा सकता है। इसका प्रचलन सैद्धान्तिक भौतिकीविद पॉल डिरैक ने किया। संकेत प्रसंस्करण के क्षेत्र में इसे प्रायः 'इकाई आवेग फलन' (unit impulse function) कहते हैं।
डिरैक डेल्टा फलन को शून्य-केंद्रित नॉर्मल-वितरण की निम्नलिखित सीमा के रूप में भी देखा जा सकता है:
δ でるた
a
(
x
)
=
1
a
π ぱい
e
−
x
2
/
a
2
{\displaystyle \delta _{a}(x)={\frac {1}{a{\sqrt {\pi }}}}\mathrm {e} ^{-x^{2}/a^{2}}}
as
a
→
0
{\displaystyle a\rightarrow 0}
δ でるた (
x
)
=
δ でるた (
−
x
)
{\displaystyle \delta (x)=\delta (-x)\,\!}
f
(
x
)
δ でるた ′
(
x
)
=
−
f
′
(
x
)
δ でるた (
x
)
{\displaystyle f(x)\delta '(x)=-f'(x)\delta (x)\,\!}
δ でるた ′
(
x
)
=
−
δ でるた ′
(
−
x
)
{\displaystyle \delta '(x)=-\delta '(-x)\,\!}
x
n
δ でるた (
x
)
=
0
∀
n
>
0
,
x
∈
R
{\displaystyle x^{n}\delta (x)=0\qquad \forall n>0,x\in \mathbb {R} \,\!}
(
x
−
a
)
n
δ でるた (
x
−
a
)
=
0
∀
n
>
0
{\displaystyle (x-a)^{n}\delta (x-a)=0\qquad \forall n>0\,\!}
δ でるた (
a
x
−
b
)
=
|
a
|
−
1
δ でるた (
x
−
(
b
/
a
)
)
∀
a
>
0
{\displaystyle \delta (ax-b)=|a|^{-1}\delta (x-(b/a))\qquad \forall a>0\,\!}
h
(
x
)
δ でるた (
x
−
a
)
=
h
(
a
)
δ でるた (
x
−
a
)
{\displaystyle h(x)\delta (x-a)=h(a)\delta (x-a)\,\!}
h
(
x
)
δ でるた ′
(
x
−
a
)
=
h
(
a
)
δ でるた ′
(
x
−
a
)
−
h
′
(
a
)
δ でるた (
x
−
a
)
{\displaystyle h(x)\delta '(x-a)=h(a)\delta '(x-a)-h'(a)\delta (x-a)\,}
δ でるた (
f
(
x
)
)
=
∑
n
|
f
′
(
x
n
)
|
−
1
δ でるた (
x
−
x
n
)
,
con
f
(
x
n
)
=
0
,
f
′
(
x
n
)
≠
0
{\displaystyle \delta (f(x))=\sum _{n}|f'(x_{n})|^{-1}\delta (x-x_{n}),\quad {\mbox{con}}\ f(x_{n})=0,\ f'(x_{n})\neq 0}
δ でるた (
ω おめが )
=
1
2
π ぱい
∫
−
∞
+
∞
e
−
i
ω おめが t
d
t
{\displaystyle \delta (\omega )={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }e^{-i\omega t}dt}
δ でるた (
r
−
r
0
)
=
{
1
r
2
sin
θ しーた
δ でるた (
r
−
r
0
)
δ でるた (
θ しーた −
θ しーた
0
)
δ でるた (
ϕ
−
ϕ
0
)
x
0
,
y
0
,
z
0
≠
0
1
2
π ぱい
r
2
sin
θ しーた
δ でるた (
r
−
r
0
)
δ でるた (
θ しーた −
θ しーた
0
)
x
0
=
y
0
=
0
,
z
0
≠
0
1
4
π ぱい
r
2
δ でるた (
r
−
r
0
)
x
0
=
y
0
=
z
0
=
0
{\displaystyle \delta (\mathbf {r} -\mathbf {r} _{0})={\begin{cases}{\frac {1}{r^{2}\sin \theta }}\delta (r-r_{0})\delta (\theta -\theta _{0})\delta (\phi -\phi _{0})&x_{0},y_{0},z_{0}\neq 0\\{\frac {1}{2\pi r^{2}\sin \theta }}\delta (r-r_{0})\delta (\theta -\theta _{0})&x_{0}=y_{0}=0,\ z_{0}\neq 0\\{\frac {1}{4\pi r^{2}}}\delta (r-r_{0})&x_{0}=y_{0}=z_{0}=0\end{cases}}}