Spazio iperbolico

In matematica, lo spazio iperbolico è uno spazio introdotto indipendentemente dai matematici Bolyai e Lobachevsky nel XIX secolo, su cui è definita una particolare geometria non euclidea, detta geometria iperbolica. Si tratta dell'esempio più importante di geometria non euclidea, assieme alla geometria ellittica.

Lo spazio iperbolico ha dimensione arbitraria $n$ ed è indicato con $\mathbb {H} ^{n}$ . Può essere realizzato tramite vari modelli equivalenti, quali ad esempio il disco, il semispazio di Poincaré o il modello dell'iperboloide. Come nella geometria euclidea, gli spazi più studiati sono il piano iperbolico $\mathbb {H} ^{2}$ e lo spazio iperbolico tridimensionale $\mathbb {H} ^{3}$ .

I modelli

Lo spazio iperbolico $\mathbb {H} ^{n}$ è un particolare spazio, su cui è definita una geometria che soddisfa i primi 4 assiomi di Euclide ma non il quinto. La geometria presente in questo spazio è detta iperbolica.

Il numero $n$ indica la dimensione dello spazio iperbolico. In ogni dimensione $n$ , lo spazio iperbolico può essere realizzato da differenti modelli, tutti equivalenti.

Modello del disco

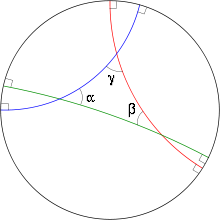
Nel modello del disco di Poincaré, lo spazio iperbolico è la palla $n$ -dimensionale

B^{n}=\{x\in \mathbb {R} ^{n}\ |\ |x|<1\}.

Per $n=2$ , questo è il cerchio di raggio unitario centrato nell'origine del piano cartesiano, senza la circonferenza di bordo.

Una retta nel disco di Poincaré è un arco di circonferenza, oppure un segmento, che interseca il bordo $\partial B^{n}$ della palla $B^{n}$ ortogonalmente in due punti. Due "rette" che si intersecano in un punto formano un angolo, e la sua ampiezza è pari all'angolo formato dalle tangenti.

Modello del semispazio

Nel modello del semispazio di Poincaré, lo spazio iperbolico è il semispazio

\{(x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}\ |\ x_{n}>0\}.

Come nel modello del disco, le rette iperboliche sono gli archi di circonferenza e le rette ortogonali al bordo. In questo modello, il bordo è l'iperpiano orizzontale $x_{n}=0$ .

Modello di Klein

Nel modello di Klein lo spazio iperbolico è (come nel modello del disco) l'insieme dei punti interni ad un cerchio $C$ . Le rette sono però segmenti veri e propri: la maggiore semplicità nel descrivere le rette viene però pagata nella descrizione degli angoli, che sono distorti rispetto agli angoli euclidei: l'angolo formato da due rette non è quello euclideo, ma dipende da questo tramite una formula opportuna.

La distanza fra due punti $P$ e $Q$ interni al disco è

d(P,Q)={\frac {1}{2}}\log {\frac {|Q-A||P-B|}{|P-A||Q-B|}}

dove $|R-S|$ è la distanza euclidea fra i punti $R$ e $S$ . I punti $A$ e $B$ sono le intersezioni fra la retta euclidea passante per $P$ e $Q$ e il bordo $\partial B^{n}$ . Il logaritmo è il logaritmo naturale. L'argomento del logaritmo è il birapporto dei quattro punti allineati.

Modello dell'iperboloide

Nel modello dell'iperboloide, lo spazio iperbolico è l'iperboloide

H={\big \{}(x_{1},\ldots ,x_{n+1})\in \mathbb {R} ^{n+1}\ {\big |}\ x_{1}^{2}+\ldots +x_{n}^{2}-x_{n+1}^{2}=-1,x_{n+1}>0{\big \}}.

In questo modello, una retta è data dall'intersezione di $H$ con un piano passante per l'origine di $\mathbb {R} ^{n+1}$ . In questo contesto, è utile definire su $\mathbb {R} ^{n+1}$ una struttura di spaziotempo di Minkowski, cioè il prodotto scalare con segnatura $(n,1)$ :

\phi {\big (}(x_{1},\ldots ,x_{n+1}),(y_{1},\ldots ,y_{n+1}){\big )}=x_{1}y_{1}+\ldots +x_{n}y_{n}-x_{n+1}y_{n+1}.

L'insieme degli $x$ aventi $\phi (x,x)=-1$ ha due componenti connesse, una delle quali (quella superiore, avente $x_{n+1}>0$ ) è l'iperboloide $H$ . La distanza fra due punti $P$ e $Q$ su $H$ è definita come

d(P,Q)=\operatorname {arcosh} (\phi (P,Q)).

Definizione univoca

La definizione più rigorosa di spazio iperbolico $\mathbb {H} ^{n}$ è la seguente: $\mathbb {H} ^{n}$ è l'unica varietà iperbolica completa e semplicemente connessa di dimensione $n$ . Una varietà iperbolica è una varietà riemanniana avente curvatura sezionale costantemente $-1$ .

Per "unica" si intende "a meno di isometrie": tutti i modelli elencati sopra sono in effetti collegati tramite isometrie, quindi definiscono concretamente la stessa varietà. Il fatto che esista un solo spazio con queste proprietà è un teorema importante in geometria differenziale.

Sottospazi

Geodetiche

Una geodetica è l'analogo della retta nel contesto euclideo. Nel modello del disco o del semispazio, le geodetiche sono archi di circonferenza o retta ortogonali al bordo (del disco o del semispazio). Le geodetiche hanno proprietà simili alle rette nella geometria euclidea:

Per ogni coppia di punti distinti passa una sola geodetica,
Per ogni punto e per ogni vettore tangente nel punto, esiste un'unica geodetica passante per il punto e tangente a questo vettore,
La geodetica che collega due punti $P$ e $Q$ è la curva con lunghezza minore fra tutte le curve che collegano i due punti. Questa lunghezza è proprio pari alla distanza $d(P,Q)$ .

Le ultime due proprietà sono valide, almeno localmente, in ogni varietà riemanniana.

Sottospazi

Come nello spazio euclideo, in quello iperbolico sono definiti, oltre alle geodetiche, spazi di dimensione superiore, come ad esempio i piani.

Un sottospazio di $\mathbb {H} ^{n}$ è un sottoinsieme $S$ tale che per ogni coppia $P$ e $Q$ di punti in $S$ l'intera geodetica passante per $P$ e $Q$ è contenuta in $S$ .

Mentre le geodetiche esistono (almeno localmente) in ogni varietà riemanniana, i sottospazi esistono solo in varietà molto particolari, quali appunto lo spazio euclideo e quello iperbolico. Come nel caso euclideo, un sottospazio di $\mathbb {H} ^{n}$ risulta essere isometrico a $\mathbb {H} ^{k}$ , per qualche $k$ . Il numero $k$ è la dimensione del sottospazio: per $k=1$ si ottiene una geodetica, per $k=2$ un piano, etc.

L'intersezione di due sottospazi è sempre un sottospazio.

Parallelismo

Lo spazio iperbolico si differenzia però nettamente da quello euclideo per la nozione di parallelismo. Dati due sottospazi $S$ e $S'$ disgiunti, esistono due nozioni di parallelismo ben distinte:

Se esiste un $k>0$ tale che $d(x,x')>k$ per ogni $x$ in $S$ e ogni $x'$ in $S'$ , allora i due spazi sono ultraparalleli.
Se non esiste un tale $k$ , i due spazi sono asintoticamente paralleli.

Nel secondo caso, esistono successioni di punti $(x_{i})$ e $(x_{i}')$ in $S$ e $S'$ le cui distanze $d(x_{i},x_{i}')$ tendono a zero. Questo fenomeno non si verifica negli spazi euclidei.

Isometrie

Una isometria di $\mathbb {H} ^{n}$ è un movimento rigido dello spazio, cioè una funzione che sposta tutti i punti dello spazio mantenendo le distanze fra questi. Le isometrie dello spazio iperbolico si comportano per molti aspetti in modo simile a quelle dello spazio euclideo. Possono inoltre essere studiate efficacemente tramite la sfera all'infinito.

Spazio omogeneo e isotropo

Nello spazio euclideo $\mathbb {R} ^{n}$ , esempi di isometrie sono le traslazioni e le rotazioni. Tramite queste isometrie è possibile spostare punti e rette a piacimento: la stessa proprietà vale anche nello spazio iperbolico: questo è infatti omogeneo e isotropo: i punti e le rette sono tutti indistinguibili. Più precisamente, per ogni coppia di punti $P$ e $Q$ , e per ogni coppia di rette $r$ e $s$ passanti rispettivamente per $P$ e $Q$ , esiste una isometria dello spazio che manda $P$ in $Q$ e $r$ in $s$ .

Sfera all'infinito

Nel modello del disco di Poincaré $B^{n}$ , la sfera all'infinito dello spazio iperbolico $\mathbb {H} ^{n}$ è il bordo $\partial B^{n}$ del disco. Come spazio topologico, ${\overline {\mathbb {H} ^{n}}}$ è omeomorfo al disco chiuso

D^{n}=\{x\in \mathbb {R} ^{n}\ |\ |x|\leq 1\}=B^{n}\cup S^{n-1}.

Si tratta quindi di uno spazio compatto. Il procedimento di compattificazione tramite aggiunta di "punti all'infinito" è simile al passaggio dallo spazio euclideo a quello proiettivo.

Tipi di isometrie

Una isometria dello spazio iperbolico

f:\mathbb {H} ^{n}\to \mathbb {H} ^{n}

si estende al bordo. Esiste cioè un unico omeomorfismo

{\bar {f}}:{\overline {\mathbb {H} ^{n}}}\to {\overline {\mathbb {H} ^{n}}}

che coincide con $f$ all'interno del disco, cioè su $\mathbb {H} ^{n}$ .

Il teorema del punto fisso di Brouwer asserisce che ogni omeomorfismo del disco chiuso $D^{n}$ in sé ha un punto fisso. Tale teorema, che non è valido sulla palla aperta $B^{n}$ , garantisce quindi l'esistenza di un punto fisso per la funzione estesa ${\bar {f}}$ (ma non per $f$ ).

Una isometria $f$ che preserva l'orientazione dello spazio iperbolico è detta:

ellittica se ha un punto fisso in $\mathbb {H} ^{n}$ ,
parabolica se non ha punti fissi in $\mathbb {H} ^{n}$ e ne ha uno al bordo $\partial \mathbb {H} ^{n}$ ,
iperbolica se non ha punti fissi in $\mathbb {H} ^{n}$ e ne ha due al bordo $\partial \mathbb {H} ^{n}$ .

Non vi sono altre possibilità oltre a quelle elencate.

Varietà iperboliche complete

Ogni varietà iperbolica completa è ottenibile come quoziente dello spazio iperbolico per un gruppo di isometrie che agisce in modo libero e propriamente discontinuo. In particolare, una tale isometria non deve avere punti fissi in $\mathbb {H} ^{n}$ .

Se la varietà iperbolica è orientabile, il gruppo è formato da isometrie che preservano l'orientazione. Tali isometrie sono quindi iperboliche o paraboliche (le ellittiche sono escluse perché hanno punti fissi in $\mathbb {H} ^{n}$ ). Se la varietà è compatta, tutte le isometrie sono iperboliche.

Piano iperbolico

Geometria iperbolica

Il piano iperbolico è lo spazio iperbolico $\mathbb {H} ^{2}$ bidimensionale. È lo spazio iperbolico più studiato, ed il primo ad essere stato introdotto storicamente, come esempio di geometria iperbolica e quindi non-euclidea. Sul piano iperbolico sono infatti validi i primi quattro assiomi di Euclide:

Tra due punti qualsiasi è possibile tracciare una ed una sola retta.
Si può prolungare una retta oltre i due punti indefinitamente.
Dato un punto e una lunghezza, è possibile descrivere un cerchio.
Tutti gli angoli retti sono uguali.

ma non è vero il quinto:

Data una qualsiasi retta

r

ed un punto

P

non appartenente ad essa, è possibile tracciare per

P

una ed una sola retta parallela alla retta

r

data.

Quest'ultimo assioma va infatti sostituito con il seguente:

Data una qualsiasi retta

r

ed un punto

P

non appartenente ad essa, è possibile tracciare per

P

infinite rette parallele alla retta

r

data.