Elettronica digitale
L'elettronica digitale è quella branca dell'elettronica che si occupa di gestire ed elaborare informazioni di tipo digitale.
Il termine digitale deriva dal termine inglese digit (cifra), per il fatto che i calcolatori elettronici operano mediante l'elaborazione di quantità numeriche elementari, i bit. Il termine è una contrazione dell'espressione inglese binary digit, che significa cifra/numero binario. Questo termine, a sua volta, deriva dal latino digitus che, nell'italiano corrente, viene tradotto con numero, per questo motivo viene definita impropriamente anche elettronica numerica.
Storia
[modifica | modifica wikitesto]
L'elettronica digitale ebbe inizio praticamente nel 1946, con un calcolatore elettronico digitale chiamato ENIAC, realizzato con circuiti a valvole. Tuttavia, l'idea che sta alla base di un computer digitale può risalire a Charles Babbage, che costruì un dispositivo meccanico di calcolo.
Il primo computer digitale venne costruito nel 1944 alla Harvard University, ma era ancora di tipo elettromeccanico, non elettronico. Anche se per molti anni il digitale rimase confinato nel settore dei computer, oggi le tecniche digitali trovano impiego in moltissime altre aree, dalla telefonia, all'elaborazione dei dati, dal radar, ai sistemi militari, dagli strumenti di uso medico, fino a prodotti di ampio mercato.
A partire dalla seconda metà del XX secolo la tecnologia digitale ha fatto grandi passi avanti, evolvendosi dalle valvole ai circuiti integrati e ai microprocessori. Inoltre si è diffusa anche nel settore televisivo, con il digitale terrestre.
Concetti chiave
[modifica | modifica wikitesto]L'elettronica digitale ha a che fare con circuiti e sistemi che funzionano gestendo due soli possibili stati di funzionamento, ad esempio due livelli di tensione, oppure due diversi livelli di corrente. Nei sistemi digitali i due diversi stati servono a rappresentare numeri, simboli, caratteri, colori, immagini, suoni e altre informazioni. Nei sistemi numerici a due stati, detti sistemi binari, le due cifre sono 0 e 1, e ciascuna di esse costituisce ciò che viene appunto chiamato bit.
Segnali logici
[modifica | modifica wikitesto]
Come si vede in figura un segnale analogico può assumere, in un determinato istante, tutti i valori continui appartenenti ad un certo intervallo di R. Un segnale digitale invece può assumere solo determinati valori, ad esempio uno alto e uno basso, come nella figura a lato, che riporta un segnale binario. La differenza fondamentale tra i due tipi di segnale è che mentre nei segnali analogici l'informazione è contenuta nella "forma" stessa del segnale, nei segnali digitali l'informazione da elaborare è codificata in serie di simboli (0 e 1). La forma del segnale non ha quindi importanza: basta che sia possibile discernere in ogni istante a quale valore logico corrisponde il segnale.
Anche un segnale digitale è fisicamente un segnale analogico. L'onda quadra perfetta mostrata in figura è in realtà un'idealizzazione matematica che nella realtà non esiste poiché il rumore la farà "fluttuare". Inoltre la relatività speciale di Einstein impedisce alle transizioni da uno stato fisico (o valore logico) all'altro di essere istantanee, ovvero con velocità di transizione infinita. Tuttavia quello che conta è che le fluttuazioni si mantengano entro un certo margine, in modo che non si perda l'informazione, ovvero si evidenzino due diversi stati fisici possibili (alto e basso) su cui costruire la logica binaria d'interesse (ad es. l'Algebra di Boole).
Perché si preferisce l'elettronica digitale a quella analogica
[modifica | modifica wikitesto]
Come detto in precedenza i segnali digitali sono anch'essi in realtà dei segnali analogici, ma ad essi sono assegnati solo i 2 livelli logici che il segnale può assumere. Tutti i segnali sono soggetti al rumore che può alterarne i valori, ma una caratteristica che distingue i circuiti digitali da quelli analogici è l'alta capacità di reiezione ai disturbi, che però, come detto prima, devono mantenersi entro un certo margine. Questa caratteristica è dovuta ad una proprietà intrinseca dei circuiti digitali, che è quella di ripristino dei livelli logici 0 e 1 dei segnali che li attraversano, pur distorto da rumore o effetti inattesi.
L'operazione di ripristino è effettuata utilizzando un circuito con funzione di trasferimento a soglia: al di sopra della soglia viene riconosciuto il bit alto, al di sotto il bit basso; in questo modo un segnale inizialmente distorto in ingresso nel passaggio attraverso questo circuito, detto interfaccia o buffer, viene ripristinato ai suoi livelli logici primitivi. L'elemento base dell'elettronica digitale è l'invertitore, che oltre a godere della proprietà di ripristino dei livelli logici, implementa la funzione logica NOT di negazione. Tramite questa configurazione, e opportune modifiche circuitali applicate ad essa, è possibile realizzare le funzioni base dell'algebra booleana ed implementare, quindi, tutte le porte e le funzioni logiche.
Nelle trasmissioni digitali inoltre l'introduzione di tecniche di codifica/decodifica di canale, possibili solo per segnali digitali, migliora ulteriormente le prestazioni rispetto agli errori. Inoltre nelle stesse trasmissioni tecniche di codifica/decodifica di sorgente riescono a diminuire la ridondanza del messaggio informativo a vantaggio della compressione di banda.
I livelli di astrazione
[modifica | modifica wikitesto]
Un sistema elettronico digitale può essere visto a diversi livelli di astrazione:
- A livello di sistema è noto ciò che il sistema deve fare ma non la sua struttura fisica. Il sistema è composto da vari elementi di processo (processing elements) che interagiscono tra di loro (utilizzando protocolli di comunicazione). A questo livello un linguaggio formale per descrivere i sistemi è il SystemC: una serie di librerie C++ open source per la modellazione e simulazione di sistemi elettronici HW/SW (https://web.archive.org/web/20081006172519/http://systemc.org/).
- A livello architetturale il sistema elettronico è un insieme di componenti più o meno standard (registri, ALU, multiplexer) connessi fra di loro. A questo livello si utilizzano linguaggi detti HDL (hardware description language) come il VHDL o il Verilog.
- A livello logico ogni componente dell'architettura è una rete logica che svolge il compito previsto. Una rete logica è un insieme di connessioni di porte logiche (AND, OR, XOR NOT, ecc.).
- A livello circuitale ogni porta logica viene realizzata tramite un circuito (il cui elemento base è il transistor). Si possono avere vari stili di realizzazione delle porte logiche a seconda del tipo di transistori che vengono usati.
- Il livello più basso è il livello di layout, in cui vengono specificate nel dettaglio le dimensioni di ogni singolo transistor e di ogni connessione.
Livello di sistema
[modifica | modifica wikitesto]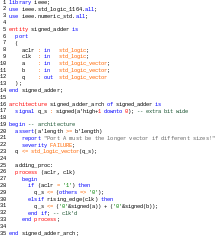
Livello architetturale
[modifica | modifica wikitesto]Livello logico
[modifica | modifica wikitesto]Si distinguono due categorie di reti logiche: reti combinatorie e reti sequenziali. Le reti combinatorie sono reti per cui le uscite dipendono solo dagli ingressi. Le reti sequenziali sono invece reti per cui le uscite dipendono sia dagli ingressi che dalla "storia" del sistema. Il sistema ha uno stato, che è un elemento di memoria e tiene conto dell'evoluzione passata del sistema.
Reti combinatorie
[modifica | modifica wikitesto]| A | B | C | X | Y |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| Funzione logica a 3 ingressi e 2 uscite | ||||
Si vogliono sintetizzare delle funzioni logiche. Utilizzando un linguaggio informale, le funzioni logiche sono delle funzioni matematiche aventi come "ingressi" e come "uscite" dei segnali logici. Le funzioni logiche possono essere espresse mediante le tavole di verità.
Esiste un teorema (teorema di Shannon) abbastanza intuitivo che permette di affermare che qualsiasi funzione logica può essere espressa come somma di prodotti degli ingressi, intendendo per somma l'operazione logica elementare OR e con prodotto l'operazione logica AND.
Ad esempio, nella figura basta vedere le combinazioni di ingressi per cui si ha Y=1:
È possibile quindi ridurre funzioni logiche complesse a combinazioni di funzioni logiche elementari.
Esistono poi dei metodi (ad esempio basati sulla Mappa di Karnaugh) che permettono di minimizzare questa scomposizione, in modo da avere una rete logica più semplice possibile.
Questo tipo di sintesi si chiama AND-OR. Per le leggi di De Morgan, è possibile fare sintesi OR-AND, NAND NAND ecc.
Componenti combinatori standard
[modifica | modifica wikitesto]
- encoder
- decoder
- multiplexer / demultiplexer
- parity checker
- majority gate
- full-adder
- half-adder
- comparatore
- Arithmetic Logic Unit
- Amplificatore tri-state
Reti sequenziali
[modifica | modifica wikitesto]
Le reti sequenziali possono essere realizzate dalle cosiddette macchine a stati. La struttura più semplice delle macchine a stati è quella delle macchine a stati di Moore. Queste sono composte da una rete combinatoria, seguita da un registro che è seguito da un'altra rete combinatoria. La prima rete combinatoria oltre agli ingressi esterni ha come ingressi le uscite del registro: si realizza così una retroazione. La macchina a stati è quindi un sistema le cui uscite dipendono sia dagli ingressi sia dallo stato del sistema stesso (rappresentato dal registro). Le reti sequenziali rappresentano quindi dispositivi con memoria. Essi sono costituiti da una opportuna combinazione di un circuito a logica combinatoria e una memoria. La memoria può essere dotata di un ingresso di clock o meno. Nel caso in cui il clock sia presente, la rete è un dispositivo sincrono, viceversa è un dispositivo asincrono.
Componenti sequenziali standard
[modifica | modifica wikitesto]- latch (ne esistono di vari tipi tipo-D, tipo-SR)
- flip-flop (tipo-D, tipo-SR, tipo-JK, tipo-T)
- contatore
- registro a scorrimento
Livello circuitale
[modifica | modifica wikitesto]
Scale d'integrazione
[modifica | modifica wikitesto]La necessità di creare funzioni logiche sempre più elaborate in spazi sempre più ridotti ha portato alla realizzazione dei circuiti integrati (IC = Integrated Circuits). Si tratta di circuiti complessi, che svolgono le funzioni elettriche di molti componenti discreti (in massima parte resistori, diodi e transistor), realizzati su singole piastrine di silicio.
In relazione al livello di integrazione è possibile fare la seguente classificazione:
- piccola scala di integrazione SSI (Small Scale Integration), se il numero di porte logiche è inferiore a 12 e non sono presenti più di 100 transistor;
- media scala di integrazione MSI (Medium Scale Integration), se il numero di porte logiche è compreso tra 12 e 100 e non sono presenti più di 1000 transistor;
- larga scala di integrazione LSI (Large Scale Integration), tra le 100 e le 1000 porte e fino a 10000 transistor;
- molto larga scala di integrazione VLSI (Very Large Scale Integration), oltre le 1000 porte e più di 100000 transistor.
Attualmente si considera anche la ULSI (Ultra Large Scale Integration) per gli integrati con più di 10000 porte.
Per integrati non digitali la scala d'integrazione è valutata considerando situazioni circuitali di complessità equivalente a quelle delle porte logiche.
Questi dispositivi integrati sono realizzati in contenitori di diverso tipo, in relazione alle diverse esigenze.
Livello di layout
[modifica | modifica wikitesto]Bibliografia
[modifica | modifica wikitesto]- F. Huré, Introduzione pratica all'impiego dei circuiti integrati digitali, Gruppo Editoriale Jackson, 1981.
- Elettronica digitale con esperimenti – Dalle porte logiche ai flip-flop, Gruppo Editoriale Jackson, 1989.
- Umberto Pellegrini, Tecniche di elettronica digitale, La Viscontea, 1979.
- Noel M. Morris, Elementi di elettronica digitale, Ulrico Hoepli, 1981.
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikizionario contiene il lemma di dizionario «elettronica digitale»
Wikizionario contiene il lemma di dizionario «elettronica digitale» Wikimedia Commons contiene immagini o altri file sull'elettronica digitale
Wikimedia Commons contiene immagini o altri file sull'elettronica digitale
| Controllo di autorità | Thesaurus BNCF 59024 · BNF (FR) cb11958744c (data) · J9U (EN, HE) 987007555316605171 |
|---|


