双曲線そうきょくせん関数かんすう

6つの双曲線そうきょくせん関数かんすう (sinh, cosh, tanh, coth, sech, csch) のグラフ

数学すうがくにおいて、双曲線そうきょくせん関数かんすう（そうきょくせんかんすう、英えい: hyperbolic function）とは、三角さんかく関数かんすうと類似るいじの関数かんすうで、標準ひょうじゅん形がたの双曲線そうきょくせんを媒介ばいかい変数へんすう表示ひょうじするときなどに現あらわれる。

概要がいよう

斜線しゃせんの領域りょういきの面積めんせきが θしーた/2 のとき、単位たんい円周えんしゅう上じょうの座標ざひょうが (cos θしーた, sin θしーた) となる。

斜線しゃせんの領域りょういきの面積めんせきが θしーた/2 のときの双曲線そうきょくせん上じょうの座標ざひょうが (cosh θしーた, sinh θしーた)

三角さんかく関数かんすうは単位たんい円周えんしゅうを用もちいて定義ていぎすることができる。

以下いか、説明せつめいを簡単かんたんにするために第だい一いち象限しょうげん（x ≥ 0 かつ y ≥ 0）の議論ぎろんに限かぎる。

単位たんい円周えんしゅう上じょうの点てん A (cos θしーた, sin θしーた) と x軸じく上じょうの点てん B(1, 0)、原点げんてん O を考かんがえる。線分せんぶん AO, BO と弧こ AB によって囲かこまれた領域りょういきの面積めんせきは θしーた/2 である。

この性質せいしつを用もちいて逆ぎゃくに三角さんかく関数かんすうを定義ていぎすることもできる。すなわち、単位たんい円周えんしゅう上じょうの点てん A と x軸じく上じょうの点てん B(1, 0) を取とり、線分せんぶん AO, BO と弧こ AB によって囲かこまれた領域りょういきの面積めんせきが θしーた/2 であるとき、A の座標ざひょうを (cos θしーた, sin θしーた) として、三角さんかく関数かんすうを定義ていぎすることができる。

単位たんい円えんの定義ていぎ式しきは

$x^{2}+y^{2}=1$

であり、標準ひょうじゅん形がたの双曲線そうきょくせんの定義ていぎ式しきは y² の符号ふごうを変かえただけの

$x^{2}-y^{2}=1$

である。単位たんい円えんの面積めんせきで三角さんかく関数かんすうを定義ていぎしたのと同おなじように双曲線そうきょくせんを用もちいて双曲線そうきょくせん関数かんすうを定義ていぎすることができる。

標準ひょうじゅん形がたの双曲線そうきょくせん上じょうの点てん A と x軸じく上じょうの点てん B(1, 0) を取とり、線分せんぶん AO, BO と双曲線そうきょくせんの囲かこむ領域りょういきの面積めんせきが θしーた/2 であるとき、A の座標ざひょうを (cosh θしーた, sinh θしーた) として、双曲線そうきょくせん関数かんすう cosh, sinh が定義ていぎされる。

ちなみに、三角さんかく関数かんすうの定義ていぎに現あらわれた θしーた は、弧こ度ど法ほうにおける角度かくどに対応たいおうしていたが、双曲線そうきょくせん関数かんすうでは角度かくどには対応たいおうしない。

このように三角さんかく関数かんすうと双曲線そうきょくせん関数かんすうは非常ひじょうに似通にかよった関数かんすうとして定義ていぎされ、いろいろな場面ばめんでその類似るいじ性せいが現あらわれる。定義ていぎに双曲線そうきょくせんを用もちいる関数かんすうを双曲線そうきょくせん関数かんすうと呼よぶことに合あわせて、定義ていぎに単位たんい円えんを用もちいる三角さんかく関数かんすうを円えん関数かんすう (circular function) と呼よぶこともある。

定義ていぎ

双曲線そうきょくせん関数かんすうは指数しすう関数かんすう e^x を用もちいて

$\sinh x={e^{x}-e^{-x} \over 2},\;\cosh x={e^{x}+e^{-x} \over 2}$

と定義ていぎされる。sinh, cosh をそれぞれ双曲線そうきょくせん正弦せいげん関数かんすう (hyperbolic sine; ハイパボリックサイン)、双曲線そうきょくせん余弦よげん関数かんすう (hyperbolic cosine; ハイパボリックコサイン) と呼よぶ。他ほかにも三さん角かく関数かんすうとの類似るいじで双曲線そうきょくせん正接せいせつ・余あまり接せっ関数かんすう

$\tanh x={\sinh x \over \cosh x},\;\coth x={1 \over \tanh x}$

や、双曲線そうきょくせん正せい割わり・余よ割わり関数かんすう

$\operatorname {sech} x={1 \over \cosh x},\;\operatorname {cosech} x={1 \over \sinh x}$

も定義ていぎできる。また、例たとえば cosh を cos hyp や ${\mathfrak {cos}}$ などと表あらわすこともあり cosech は長ながいので csch と書かくこともある。

このように定義ていぎされた、双曲線そうきょくせん正弦せいげん関数かんすう、双曲線そうきょくせん余弦よげん関数かんすう、双曲線そうきょくせん正接せいせつ関数かんすう、双曲線そうきょくせん余あまり接せっ関数かんすう、双曲線そうきょくせん正せい割わり関数かんすう、双曲線そうきょくせん余よ割わり関数かんすうを総称そうしょうして双曲線そうきょくせん関数かんすうという。

指数しすう関数かんすう e^x は x を複素ふくそ変数へんすうに拡張かくちょうできるので、指数しすう関数かんすうで定義ていぎされている双曲線そうきょくせん関数かんすう自体じたいも x を複素ふくそ変数へんすうにとってもよい。

双曲線そうきょくせん関数かんすうはいずれも名称めいしょうが長ながいため、読よむときは省略しょうりゃくされて、sinh はシャインあるいはシンチ、cosh はコッシュあるいはコシャイン、tanh はタンチとも読よまれる。

記号きごうとしての sinh, cosh , tanh はヨハン・ハインリヒ・ランベルトが導入どうにゅうした。

性質せいしつ

基本きほん性質せいしつ

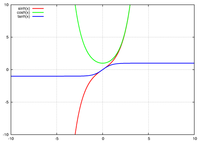sinh, cosh と tanh のグラフ。特とくに cosh x のグラフは懸垂けんすい線せんとして知しられている。

csch, sech と coth のグラフ

指数しすう関数かんすうを偶関数すうの部分ぶぶんと奇き関数かんすうの部分ぶぶんに分わけたとき、

${\begin{aligned}e^{x}&=\cosh x+\sinh x\\e^{-x}&=\cosh x-\sinh x\end{aligned}}$

となり、偶関数すう部分ぶぶんが cosh x で、奇き関数かんすう部分ぶぶんが sinh x であることが分わかる。 また (cosh x, sinh x) は、双曲線そうきょくせん x² − y² = 1 上うえの点てんであり

$\cosh ^{2}x-\sinh ^{2}x=1$

が成なり立たつ。

加法かほう定理ていり

三角さんかく関数かんすうの場合ばあいと同様どうように次つぎの加法かほう定理ていりが成立せいりつする。

${\begin{aligned}\sinh(\alpha +\beta )&=\sinh \alpha \cosh \beta +\cosh \alpha \sinh \beta \\\sinh(\alpha -\beta )&=\sinh \alpha \cosh \beta -\cosh \alpha \sinh \beta \\\cosh(\alpha +\beta )&=\cosh \alpha \cosh \beta +\sinh \alpha \sinh \beta \\\cosh(\alpha -\beta )&=\cosh \alpha \cosh \beta -\sinh \alpha \sinh \beta \\\tanh(\alpha +\beta )&={\frac {\tanh \alpha +\tanh \beta }{1+\tanh \alpha \tanh \beta }}\\\tanh(\alpha -\beta )&={\frac {\tanh \alpha -\tanh \beta }{1-\tanh \alpha \tanh \beta }}\end{aligned}}$

微分びぶん公式こうしき

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\sinh x&=\cosh x\\{\frac {\mathrm {d} }{\mathrm {d} x}}\cosh x&=\sinh x\\{\frac {\mathrm {d} }{\mathrm {d} x}}\tanh x&=1-\tanh ^{2}x=\operatorname {sech} ^{2}x={\frac {1}{\cosh ^{2}x}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\coth x&=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-{\frac {1}{\sinh ^{2}x}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {csch} x&=-\coth x\operatorname {csch} x\\{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sech} x&=-\tanh x\operatorname {sech} x\end{aligned}}$

したがって、sinh x と cosh x はいずれも二に階かいの線型せんけい微分びぶん方程式ほうていしき

${{\rm {d}}^{2} \over {\rm {d}}x^{2}}y(x)=y(x)$

の解かいであり、この微分びぶん方程式ほうていしきの基本きほん解かい系けいの一ひとつになる。

冪べき級数きゅうすう展開てんかい

双曲線そうきょくせん関数かんすうのテイラー展開てんかいあるいはローラン展開てんかいは、以下いかの式しきで与あたえられる。ただし、B_n, E_n はそれぞれベルヌーイ数すう (B₂ = 1/6, B₄ = −1/30, …)、オイラー数すう (E₀ = 1, E₂ = −1, …) である。

${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\dotsb \\[1ex]\cosh x&=\sum _{n=0}^{\infty }{x^{2n} \over (2n)!}=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\dotsb \\[1ex]\tanh x&=\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\dotsb ,\quad |x|<{\frac {\pi }{2}}\\[1ex]\operatorname {csch} x&={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}}={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\dotsb ,\quad 0<|x|<\pi \\[1ex]\operatorname {sech} x&=\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}}=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\dotsb ,\quad |x|<{\frac {\pi }{2}}\\[1ex]\coth x&={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}}={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\dotsb ,\quad 0<|x|<\pi \end{aligned}}$

無限むげん乗じょう積せき展開てんかい

双曲線そうきょくせん関数かんすうは以下いかに示しめす無限むげん乗じょう積せきに展開てんかいされる。(→証明しょうめい)

${\begin{aligned}\sinh(\pi z)&=\pi z\prod _{n=1}^{\infty }\left(1+{\frac {z^{2}}{n^{2}}}\right)\\\cosh(\pi z)&=\prod _{n=1}^{\infty }\left(1+{\frac {z^{2}}{(n-1/2)^{2}}}\right)\end{aligned}}$

三角さんかく関数かんすうとの関係かんけい

複素ふくそ変数へんすうで定義ていぎされた三角さんかく関数かんすうと双曲線そうきょくせん関数かんすうを比くらべてみると

${\begin{aligned}\sinh x&=-i\sin(ix)\\\cosh x&=\cos(ix)\end{aligned}}$

という関係かんけいにある。

これは、それぞれの指数しすう関数かんすうによる表現ひょうげんの比較ひかく、テイラー展開てんかいの比較ひかくなどによって導出どうしゅつすることができる。

逆ぎゃく双曲線そうきょくせん関数かんすう

詳細しょうさいは「逆ぎゃく双曲線そうきょくせん関数かんすう」を参照さんしょう

双曲線そうきょくせん関数かんすうが指数しすう関数かんすうで表あらわせるように、その逆ぎゃく関数かんすうである逆ぎゃく双曲線そうきょくせん関数かんすうは対数たいすう関数かんすうを用もちいて表示ひょうじすることができる。等式とうしき x = sinh y や x = cosh y などを考かんがえれば、これらは e^y に関かんする二に次じ方程式ほうていしきであるから解とくことができて、次つぎの表示ひょうじを得える。

${\begin{aligned}\sinh ^{-1}x&=\log \left(x+{\sqrt {x^{2}+1}}\right)\\\cosh ^{-1}x&=\log \left(x+{\sqrt {x^{2}-1}}\right)\\\tanh ^{-1}x&={\frac {1}{2}}\log {\frac {1+x}{1-x}}\end{aligned}}$

逆ぎゃく関数かんすう sinh⁻¹, cosh⁻¹ などはそれぞれ area sin hyp, area cos hyp （area は「面積めんせき」の意い）もしくはそれを略りゃくして ar sinh, ar cosh と書かいたり、逆ぎゃく三角さんかく関数かんすうと同様どうように arcsinh, arccosh などと書かいたりすることもある。

微分びぶん公式こうしき

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\sinh ^{-1}x&={\frac {1}{\sqrt {x^{2}+1}}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\cosh ^{-1}x&={\frac {1}{\sqrt {x^{2}-1}}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\tanh ^{-1}x&={\frac {1}{1-x^{2}}}\end{aligned}}$

このことから、(1 − x²)^1/2 を含ふくむ有理ゆうり関数かんすうの原始げんし関数かんすうを求もとめるために x = sin t などと三角さんかく関数かんすうを用もちいた置換ちかん積分せきぶんを考かんがえると有用ゆうようである場合ばあいが多おおいのと同様どうように、(x² + 1)^1/2 を含ふくむ有理ゆうり関数かんすうの積分せきぶんに双曲線そうきょくせん関数かんすうを用もちいた置換ちかん積分せきぶんを考かんがえることは有用ゆうようであることが多おおい。

• 
  arcsinh のグラフ
• 
  arccosh のグラフ
• 
  arctanh のグラフ

関連かんれん項目こうもく

• 三角さんかく関数かんすう
• 媒介ばいかい変数へんすう
• 指数しすう関数かんすう
• カテナリー曲線きょくせん - cosh
• シグモイド関数かんすう、ロジスティック関数かんすう - tanh
• 双曲線そうきょくせん正せい割わり分布ぶんぷ - sech
• グーデルマン関数かんすう - 双曲線そうきょくせん関数かんすうと三角さんかく関数かんすうの組合くみあわせ
• 双曲線そうきょくせん関数かんすうの原始げんし関数かんすうの一覧いちらん

外部がいぶリンク

• 『双曲線そうきょくせん関数かんすう(sinh,cosh,tanh)の意味いみ・性質せいしつ・楽たのしい話題わだいまとめ』 - 高校こうこう数学すうがくの美うつくしい物語ものがたり
• Weisstein, Eric W. "Hyperbolic functions". mathworld.wolfram.com (英語えいご).