스토크스 현상

복소해석학에서 스토크스 현상(Stokes現象げんしょう, 영어: Stokes phenomenon)은 전해석 함수의 점근적 근사가 분지절단을 보이는 현상이다.

정의

어떤 전해석 함수 $f\colon \mathbb {C} \to \mathbb {C}$ 가 $|z|\gg 1$ 에 대하여 다음과 같이 근사된다고 하자.

f(z)\approx g(z)\qquad (|z|\gg 1)

여기서 $g(z)$ 는 전해석 함수가 아니며, 분지절단을 가질 수 있다. 이 경우, $f$ 가 스토크스 현상을 보인다고 한다.

예

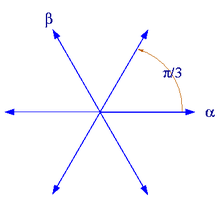
에어리 함수 $\operatorname {Ai} (z)$ 는 ${\widehat {\infty }}$ 에서 본질적 특이점을 갖는 전해석 함수이다. 임의의 편각 $\operatorname {arg} z$ 에 대하여, 에어리 함수는 다음과 같이 근사된다.

\operatorname {Ai} (z)\sim C_{+}x^{-1/4}\exp(+(2/3)x^{3/2})+C_{-}x^{-1/4}\exp(-(2/3)x^{3/2})

이 근삿값은 전해석 함수가 아니므로, 스토크스 현상이 발생하는 것을 볼 수 있다.

이와 같이, 일반적으로 점근적 근사는 여러 개의 점근적 항으로 구성되어 있다. 대부분의 편각에서는 이 항 가운데 하나만이 지수적으로 우세하게 되고, 따라서 나머지 항들은 버릴 수 있다. 여러 항들의 크기가 일치하게 되는 점들을 반 스토크스 선(영어: anti-Stokes line)이라고 한다. 이러한 점에서는 점근적 근사의 우세한 항이 바뀌게 된다.

열등한 항의 계수는 스토크스 선(영어: Stokes line)에서 급격한 변화를 겪는다. 스토크스 선은 우세한 항이 열등한 항보다 상대적으로 가장 큰 값을 갖는 선이다.

$\operatorname {Ai} (z)$ 의 스토크스 선들은

\operatorname {arg} (z)=2n\pi /3\qquad (n\in \mathbb {Z} )

이며, 반 스토크스 선들은

\operatorname {arg} (z)=(2n+1)\pi /3\qquad (n\in \mathbb {Z} )

이다. 스토크스 선 근처에서 $C_{+}$ 와 $C_{-}$ 의 값은 급격히 변할 수 있다.

역사

조지 가브리엘 스토크스가 에어리 함수를 연구하는 과정에서 발견하였다.^[1]^[2]^[3]

같이 보기

보렐 합

각주

↑ Stokes, G. G. (1851). “On the numerical Calculation of a Class of Definite Integrals and Infinite Series”. 《Transactions of the Cambridge Philosophical Society》 (영어) 9 (1): 166–187. Bibcode:1851TCaPS...9..166S.
↑ Stokes, G. G. (1858). “On the Discontinuity of Arbitrary Constants which appear in Divergent Developments”. 《Transactions of the Cambridge Philosophical Society》 (영어) 10 (1): 105–128. Bibcode:1864TCaPS..10..105S.
↑ Stokes, G. G. (1869). “Supplement to a paper on the Discontinuity of Arbitrary Constants which appear in Divergent Developments”. 《Transactions of the Cambridge Philosophical Society》 (영어) 11 (2): 412-425. JFM 02.0163.03.

Kowalenko, Victor (2009). 《The Stokes phenomenon, Borel summation and Mellin-Barnes regularisation》 (영어). Bentham. doi:10.2174/97816080501091090101. ISBN 978-1-60805-097-0.
Meyer, R. E. (1989년 9월). “A simple explanation of the Stokes phenomenon”. 《Society for Industrial and Applied Mathematics Review》 (영어) 31 (3): 435–445. doi:10.1137/1031090. JSTOR 2031404. Zbl 0679.34068.
Sabbah, Claude (2013). 《Introduction to Stokes structures》. Lecture Notes in Mathematics (영어) 2060. Springer. arXiv:0912.2762. Bibcode:2009arXiv0912.2762S. doi:10.1007/978-3-642-31695-1. ISBN 978-3-642-31694-4. ISSN 0075-8434. Zbl 1260.34002.
Berry, M. V. (1988). “Stokes’ phenomenon; smoothing a Victorian discontinuity”. 《Publications Mathématiques de l’Institut des Hautes Études Scientifiques》 (영어) 68 (1): 211-221. doi:10.1007/BF02698550. ISSN 0073-8301. MR 1001456. Zbl 0701.58012.
Mariño, Marcos (2012). “Lectures on non-perturbative effects in large N gauge theories, matrix models and strings” (영어). arXiv:1206.6272. Bibcode:2012arXiv1206.6272M.

외부 링크

“Stokes phenomenon”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
Weisstein, Eric Wolfgang. “Stokes phenomenon”. 《Wolfram MathWorld》 (영어). Wolfram Research.
“Stokes phenomenon”. 《nLab》 (영어).

[1] Stokes, G. G. (1851). “On the numerical Calculation of a Class of Definite Integrals and Infinite Series”. 《Transactions of the Cambridge Philosophical Society》 (영어) 9 (1): 166–187. Bibcode:1851TCaPS...9..166S.

[2] Stokes, G. G. (1858). “On the Discontinuity of Arbitrary Constants which appear in Divergent Developments”. 《Transactions of the Cambridge Philosophical Society》 (영어) 10 (1): 105–128. Bibcode:1864TCaPS..10..105S.

[3] Stokes, G. G. (1869). “Supplement to a paper on the Discontinuity of Arbitrary Constants which appear in Divergent Developments”. 《Transactions of the Cambridge Philosophical Society》 (영어) 11 (2): 412-425. JFM 02.0163.03.

[1]

[2]

[3]