Algorytm Aho-Corasick

Rodzaj	wyszukiwanie wzorca
	Złożoność
Czasowa

Algorytm Aho-Corasick jest jednym z algorytmów wyszukiwania wzorca w tekście opracowanym przez Alfreda V. Aho oraz Margaret J. Corasick. Znajduje on w tekście wystąpienia słów ze słownika (pewnego zadanego zbioru wzorców). Wszystkie wzorce są szukane jednocześnie, co powoduje, że złożoność obliczeniowa algorytmu jest liniowa względem sumy długości wzorców, długości tekstu i liczby wystąpień wzorców w tekście. W tekście może jednak występować nawet kwadratowa od długości tekstu liczba wystąpień wzorców (np. gdy słownikiem jest a, aa, aaa, aaaa, zaś tekstem jest aaaa).

Ideą algorytmu jest stworzenie Drzewa trie o sufiksowych połączeniach pomiędzy wierzchołkami reprezentującymi różne słowa (niekoniecznie znajdujące się w słowniku). Inaczej mówiąc tworzone jest drzewo o etykietowanych krawędziach w którym każdy wierzchołek reprezentuje pewne słowo, składające się ze złączonych etykiet krawędzi znajdujących się na ścieżce od korzenia do tego węzła. Dodatkowo dołączane są krawędzie od wierzchołka do innego wierzchołka reprezentującego jego najdłuższy sufiks (tzw. fail) W czasie wyszukiwania w tekście algorytm porusza się po tym drzewie zaczynając od korzenia i przechodząc do wierzchołka po krawędzi etykietowanej znakiem odczytanym z tekstu. W przypadku gdy takiej nie ma w drzewie, algorytm korzysta z krawędzi fail i tam próbuje przejść do wierzchołka po krawędzi etykietowanej odczytanym znakiem. W przypadku natrafienia na węzeł oznaczony jako koniec słowa, algorytm wypisuje je jako znalezione w tekście oraz sprawdza, czy czasem w tym miejscu nie kończy się więcej wzorców przechodząc krawędziami fail aż do korzenia, sprawdzając, czy nie przechodzi po wierzchołku będącym końcem wzorca.

Jednym z programów wykorzystujących ten algorytm jest polecenie systemu Unix – fgrep.

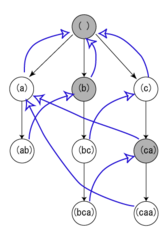
Przykładowy słownik oraz drzewo trie (szare węzły odpowiadają słowom niewystępującym w słowniku, niebieskie krawędzie wskazują najdłuższy sufiks słowa).

Słownik { a, ab, bc, bca, c, caa }

Ścieżka Czy węzeł jest w słowniku Najdłuższy sufiks będący w drzewie Sufiks będący innym wzorcem

() –

(a) + ()

(ab) + (b)

(b) – ()

(bc) + (c) (c)

(bca) + (ca) (a)

(c) + ()

(ca) – (a) (a)

(caa) + (a) (a)

Opis wyszukiwania wzorców w tekście abccab

Wyszukiwanie wzorców w tekście abccab

Węzeł Tekst do przeglądnięcia Wyjście programu:Pozycja w słowie Przejście Wyjście programu

() abccab rozpoczęcie w korzeniu

(a) bccab a:1 () do potomka (a) Obecny węzeł

(ab) ccab ab:2 (a) do potomka (ab) Obecny węzeł

(bc) cab bc:3, c:3 (ab) do sufiksu (b) do potomka (bc) Obecny węzeł, Węzeł sufiksowy ze słownika

(c) ab c:4 (bc) do sufiksu (c) do sufiksu () do potomka (c) Obecny węzeł

(ca) b a:5 (c) do potomka (ca) Węzeł sufiksowy ze słownika

(ab) ab:6 (ca) do sufiksu (a) do potomka (ab) Obecny węzeł

Algorytm tworzenia automatu

Dane są trzy funkcje:

NEXT(węzeł, litera) – funkcja przejścia definiująca, z którym węzłem jest połączony przez krawędź etykietowaną literą, np. NEXT("bc", 'a') ⇒ "bca", natomiast NEXT("ca", 'b') ⇒ NIL.
FAIL(węzeł) – funkcja określająca węzeł połączony przez krawędź fail.
OUTPUT(węzeł) – zbiór napisów powiązanych z węzłem.

Algorytm składa się z dwóch głównych kroków:

utworzenia drzewa trie, dla wszystkich napisów na tym etapie ustalane są wartości funkcji NEXT oraz OUTPUT;
uzupełnienie krawędzi fail (czyli określenie funkcji FAIL).

Uzupełnianie krawędzi fail

Drzewo trie przeglądane jest poziomami (wszerz) – mając zdefiniowane FAIL dla wszystkich węzłów na poziomie P-1 i wcześniejszych, można znaleźć wartości FAIL oraz OUTPUT dla węzłów z poziomu P.

W pierwszym kroku uzupełnia się FAIL dla węzłów z poziomu pierwszego (czyli następników korzenia), po czym przeglądane są kolejne poziomy.

procedure Aho-Corasick-tworzenie-fail(trie)
   kolejka := pusta kolejka
   korzeń  := korzeń drzewa trie

   { etap 1 }
   for litera in alfabet do
      węzeł = NEXT(korzeń, litera)
      if węzeł <> nil then
         { powiąż krawędzią fail }
         FAIL(węzeł) = korzeń

         dodaj węzeł do kolejki
      else
         { określenie funkcji NEXT korzenia dla każdej litery }
         NEXT(korzeń, litera) = korzeń
      end
   end

   { etap 2 }
   while kolejka nie pusta do
      węzeł = weź z kolejki
      for litera in alfabet do
         następnik = NEXT(węzeł, litera)
         if następnik <> nil then
            dodaj następnik do kolejki

            x := FAIL(węzeł)
            while NEXT(x, litera) = nil do
               x := FAIL(x)
            end

            FAIL(następnik) := NEXT(x, litera)
            OUTPUT(następnik) := OUTPUT(następnik) + OUTPUT(NEXT(x, litera))
         end
      end
   end

Algorytm wyszukiwania

procedure Aho-Corasick-wyszukiwanie(napis, trie)
   begin
      węzeł = korzeń drzewa trie
      for i := 1 to długość napisu do
         litera := napis[i]

         while NEXT(węzeł, litera) = nil do
            węzeł := FAIL(węzeł)
         end

         węzeł := NEXT(węzeł, litera)
         if OUTPUT(węzeł) <> nil then
            wypisz pozycję i
            wypisz wszystkie wartości ze zbioru OUTPUT(węzeł)
         end
      end
   end

Determinizacja automatu

Przy przetwarzaniu jednego znaku może być odwiedzone więcej niż jeden węzeł, tj. najpierw pewna liczba przejść przez krawędzie fail, a następnie przez jedną krawędź etykietowaną literą. Automat można jednak zdeterminizować, tj. zrezygnować z krawędzi fail i określić dla każdego węzła następnik, dzięki czemu dla jednej litery automat zmieni stan dokładnie raz. Wiąże się to jednak ze znacznym wzrostem wymagań pamięciowych.

Dla odróżnienia nowa funkcja przejść nazwana została DETNEXT.

procedure Aho-Corasick-determinizacja(trie)
   begin
      kolejka := pusta kolejka
      węzeł := korzeń drzewa trie

      for litera in alfabet do
         węzeł := NEXT(korzeń, litera)

         if węzeł <> korzeń then
            dodaj węzeł do kolejki
         end

         DETNEXT(korzeń, litera) := węzeł
      end

      while kolejka nie pusta do
         węzeł := weź z kolejki

         { wykonanie fragmentu procedury Aho-Corasick-wyszukiwanie }
         for litera in alfabet:
            { dla liter alfabetu, dla których NEXT jest nieokreślony (NIL) }
            if NEXT(węzeł, litera) = nil then
               DETNEXT(węzeł, litera) := DETNEXT(FAIL(węzeł), litera)
            { lub skopiowanie istniejącego przejścia }
            else
               x = NEXT(węzeł, litera)
               DETNEXT(węzeł, litera) = x
               dodaj x do kolejki
            end
         end
      end
   end

Wówczas algorytm wyszukiwania upraszcza się do:

procedure Aho-Corasick-wyszukaj-w-deterministycznym(napis, trie)
   begin
      węzeł = korzeń drzewa trie
      for i := 1 to długość napisu do
         litera := napis[i]
         węzeł  := DETNEXT(węzeł, litera)

         if OUTPUT(węzeł) <> nil then
            wypisz pozycję i
            wypisz wszystkie wartości ze zbioru OUTPUT(węzeł)
         end
      end
   end

Bibliografia

Alfred V. Aho, Margaret J. Corasick. Efficient string matching: An aid to bibliographic search. „Communications of the ACM”. 18 (6), s. 333–340, 1975. DOI: 10.1145/360825.360855.

Linki zewnętrzne

Implementacja w Perlu
Implementacja w Pythonie na licencji GPLv2 lub nowszej. hkn.eecs.berkeley.edu. [zarchiwizowane z tego adresu (2009-01-18)].
Darmowa implementacja w C