Domki i studnie

Domki i studnie[2] – zagadka matematyczna, której współczesna wersja może mieć następujące brzmienie:
Na kartce (płaszczyźnie) są 3 domki i 3 firmy (doprowadzające wodę, prąd i gaz). Bez użycia trzeciego wymiaru i bez przechodzenia przez domki ani przez firmy, doprowadź wodę, prąd i gaz do każdego domku, tak aby linie się nie przecięły.
Formalnie łamigłówka odpowiada na pytanie czy pełny graf dwudzielny jest płaski[2].
Historia
[edytuj | edytuj kod]Przegląd historii zagadki podał David E. Kullman w 1979 stwierdzając, że większość publikacji na temat tego problemu określa go jako „starożytny”[4]. Najwcześniejszą wersję, którą odnalazł Kullman, opublikował Henry Ernest Dudeney w 1917[1]. Tę samą zagadkę Dudeney opublikował wcześniej w 1913 w The Strand Magazine podkreślając, że jest ona bardzo stara, lecz ją uwspółcześnił dzięki zastosowaniu „wody, gazu i elektryczności”[5].
W innych starych wersjach zagadki należało wytyczyć ścieżki od trzech domów do trzech studni[6], kościoła, knajpy i studni[7] lub gołębnika, studni i brogu[8].
Zagadka stała się motywacją w teorii grafów nad wprowadzeniem pojęcia grafu planarnego[9].
Rozwiązanie
[edytuj | edytuj kod]
Nie istnieje rozwiązanie pozwalające na wyznaczenie dziewięciu połączeń, w którym linie by się nie przecinały[2]. Treść zagadki sprowadza się do utworzenia pełnego dwudzielnego grafu [2]. Dowód nierozwiązywalności zagadki sprowadza się do wykazania, że nie jest planarny[2]. Ów graf wraz z są elementarnymi grafami nieplanarnymi[2]. W 1930 Kazimierz Kuratowski opublikował twierdzenie, w którym stwierdził, że graf jest planarny jeśli nie zawiera w sobie lub [10].
Inne powierzchnie
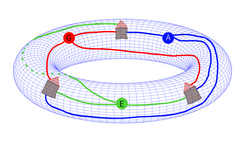
[edytuj | edytuj kod]Możliwość rozrysowania grafu bez przecięć zależy od rozmaitości topologicznej, na której jest on umieszczany[11]. Takim przykładem jest torus, na którym graf można narysować bez przecinających się linii[11].
Przypisy
[edytuj | edytuj kod]- ↑ a b Dudeney 1917 ↓.
- ↑ a b c d e f Jaszuńska 2011 ↓.
- ↑ Marta Bilska, Rozwiązanie zagadki o trzech domkach, [w:] Korepetycje z Martą [online], YouTube, 16 lutego 2016 [dostęp 2018-04-24] (pol.).
- ↑ Kullman 1979 ↓, s. 299.
- ↑ Dudeney 1913 ↓.
- ↑ Puzzle, „Successful Farming”, 13, 1914, s. 50 (ang.).
- ↑ Wykład 13. Grafy planarne [online] [dostęp 2020-02-08].
- ↑ Jerzy Mioduszewski, Wykłady z topologii. Topologia przestrzeni euklidesowych, Katowice: Wydawnictwo Uniwersytetu Śląskiego, 1994, s. 33, za Hugo Steinhaus, Kalejdoskop matematyczny, 1956, s. 261.
- ↑ 7. Planar Graphs, [w:] Sudev Naduvath, Lecture notes on graph teory, Thrissur, India: Centre for Studies in Discrete Mathematics, 2017, s. 81, ISBN 978-93-5291-147-9 (ang.).
- ↑ Kuratowski 1930 ↓.
- ↑ a b Sydow ↓.
Bibliografia
[edytuj | edytuj kod]- Joanna Jaszuńska, Domki i studnie, „Delta” (8), sierpień 2011, s. 25 (pol.).
- David E. Kullman, The Utilities Problem, „Mathematics Magazine”, 52 (5), listopad 1979, s. 299–302, JSTOR: 2689782 (ang.).
- 251. - Water, gas and electricity, [w:] Henry Ernest Dudeney, Amusements in mathematics, 1917, s. 73.
- Henry Dudeney, Perplexities, with some easy puzzles for beginners, „The Strand Magazine”, 46, 1913, s. 110.
- Kazimierz Kuratowski, Sur le problème des courbes gauches en topologie, „Fundamenta Mathematicae”, 15, 1930, s. 271–283 (fr.).
- Inne powierzchnie, [w:] Marcin Sydow, Grafy i Zastosowania. 7: Planarność, s. 17.
Linki zewnętrzne
[edytuj | edytuj kod]- Planar Graphs, [w:] Numberphile [online], YouTube, 11 listopada 2019 [dostęp 2019-11-12] (ang.).
- Eric W. Weisstein, Utility Graph, [w:] MathWorld, Wolfram Research [dostęp 2020-12-17] (ang.).


