Wielotaśmowa maszyna Turinga
Wielotaśmowa maszyna Turinga (ang. multitape Turing machine) jest jak zwykła maszyna Turinga z tą różnicą, że ma wiele taśm. Każda taśma ma własną głowicę do zapisu i odczytu danych. Początkowo dane wejściowe zapisane są na taśmie pierwszej, a pozostałe taśmy są puste[1].
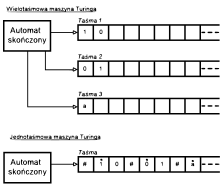
W niektórych publikacjach naukowych wielotaśmowa maszyna Turinga nazywana jest także maszyną Turinga z wieloma ciągami i kursorami, gdzie ciągi to innymi słowy taśmy, natomiast kursory to głowice[2].
Każdą wielotaśmową maszynę Turinga działającą w czasie niezależnie od liczby taśm, można zasymulować za pomocą jednotaśmowej maszyny Turinga w czasie [2]. Ponadto żadna z klas złożoności (np. czasu wielomianowego) nie podlega zmianom, a zatem zarówno w modelu jednotaśmowym, jak i wielotaśmowym są one takie same.
Zapis formalny
[edytuj | edytuj kod]Maszyna Turinga z -taśmami może być opisana jako gdzie:
- – skończony zbiór stanów,
- – skończony zbiór symboli wejściowych,
- – skończony zbiór dopuszczalnych symboli,
- – stan początkowy,
- – symbol pusty, który należy do zbioru dopuszczalnych symboli, ale nie może być symbolem wejściowym,
- – zbiór stanów końcowych,
- – funkcja częściowa, zwana funkcją przejść, gdzie jest liczbą taśm, to przesunięcie w lewo, przesunięcie w prawo, a to brak przesunięcia.
Maszyna Turinga z dwoma stosami
[edytuj | edytuj kod]Maszyna Turinga z dwoma stosami (ang. two-stack Turing machine) – to deterministyczna maszyna Turinga z taśmą wejściową służącą tylko do odczytu, oraz dwiema taśmami pamięci. Jeżeli na którejkolwiek z taśm pamięci głowica przesuwa się w lewo, to na danej taśmie drukowany jest symbol pusty.
Przetwornik ciągów skończonych
[edytuj | edytuj kod]Specjalnym przypadkiem wielotaśmowej maszyny Turinga jest maszyna posiadająca trzy taśmy: roboczą, wejściową i wyjściową. Na taśmie wejściowej umieszczone jest słowo wejściowe tylko do odczytu, bez możliwości zmiany zawartości komórek. Na taśmie wyjściowej w chwili początkowej umieszczone są wyłącznie symbole puste, a w trakcie wykonywania programu w komórkach zapisywane są pewne symbole wynikające z prowadzonych obliczeń[3].
Zobacz też
[edytuj | edytuj kod]Przypisy
[edytuj | edytuj kod]- ↑ Michael. Sipser, Introduction to the theory of computation, wyd. 2nd ed, Boston: Thomson Course Technology, 2006, ISBN 0-534-95097-3, OCLC 58544333 [dostęp 2018-11-26].
- ↑ a b Kanarek i inni, Złożoność obliczeniowa, wyd. 2, Warszawa: Wydawnictwa Naukowo-Techniczne, 2007, ISBN 978-83-204-3335-7, OCLC 749799507 [dostęp 2019-01-14].
- ↑ Bolesław Mikołajczak, Janusz Stokłosa, Złożoność obliczeniowa algorytmów, Instytut Podstaw Informatyki Polskiej Akademii Nauk, 1983 [dostęp 2019-01-12] (pol.).














