Kleinflaska

En handblåst kleinflaska

Kleinflaska eller kleinyta som det först kallades, är en konstruktion som fascinerat människor sedan den beskrevs första gången år 1882 av matematikern Felix Klein efter vilken den också är uppkallad. Kleinflaska är egentligen inte en flaska i ordets rätta mening utan en ensidig yta, där man antingen kan se det som att den saknar yttre eller inre yta eller där den tänkta inre/yttre ytan är samma. Ett möbiusband är ett band med endast en yta och en kantlinje. En kleinflaska är som ett möbiusband, men utan kantlinje. Det går enkelt att "bevisa" att den bara har en kontinuerlig yta genom att dra ett streck på "alla" ytor utan att lyfta pennan (något man inte kan göra på ett vanligt band).

Utseende

En kleinflaska är en icke-orienterbar yta. Ett sådant fenomen kan förklaras som att en yta som har en väg som gör att en tänkt vägfarare kommer tillbaka till samma punkt men spegelvänt. Ytan skiljer sig då till exempel ifrån en sfär, där man om man rör sig i en riktning kommer tillbaka till samma punkt men inte spegelvänt. Att den tänkta vägfararen skulle återkomma spegelvänt om vägfararen går längs den icke-orienterbara ytan låter måhända väldigt konstigt men det kan enkelt förklaras genom att jämföra ett möbiusband med en sfär eller ett vanligt band. Går vägfararen ett varv längs en sfär, kan man lätt se framför sig att vägfararen går ett varv runt jorden och återkommer till samma ställe. Går vägfararen ett varv längs ett möbiusband återkommer vägfararen till samma punkt men på andra sidan bandet det vill säga spegelvänt. En kleinflaska fungerar likadant men den har till skillnad från möbiusbandet, ingen kantlinje (vilket en sfär inte heller har).

Konstruktion

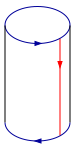
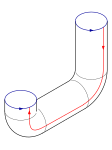
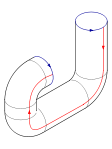
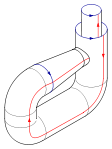
Nedan visas ett exempel på hur en kleinflaska kan skapas. Man använder sig oftast av flera cylindrar som man sätter ihop ungefär som nedan. Problemet med detta är då att ytorna(ytan) skär varandra. En "verklig" kleinflaska har inga skärningar med sig själv. Detta kan dock endast göras i fyra dimensioner så vi som lever i tre dimensioner får nöja oss med att ha en kleinflaska som skär sig själv (utan att den för den delen blir mindre intressant). En kleinflaska kan konstrueras genom att ta två möbiusband och länka ihop dessa. Kleinflaskan kan sedan givetvis också sönderdelas i möbiusband.

En torus är inte en kleinflaska, men vi kan dock skapa en kleinflaska av en torus (men det är mer korrekt att säga att man gör en kleinflaska utifrån en cylinder)

• 
• 
• 
• 
• 
• 
• 

Denna form av kleinflaska är tämligen svår och krånglig att uttrycka rent matematiskt, men nedan finns en annan variant, nämligen den "8"-formiga kleinflaskan.

• 

Denna variant kan även uttryckas relativt enkelt matematiskt genom parametrisering av x,y och z axlarna

$x(u,v)=\left[a+\cos \left({\tfrac {1}{2}}u\right)\sin(v)-\sin \left({\tfrac {1}{2}}u\right)\sin(2v)\right]\cos(u)$

$y(u,v)=\left[a+\cos \left({\tfrac {1}{2}}u\right)\sin(v)-\sin \left({\tfrac {1}{2}}u\right)\sin(2v)\right]\sin(u)$

$z(u,v)=\sin \left({\tfrac {1}{2}}u\right)\sin(v)+\cos \left({\tfrac {1}{2}}u\right)\sin(2v)$

där $u\in [0,2\pi ],v\in [0,2\pi ]$ och $a>2$

Övrigt

Kleinflaskan hette egentligen Kleinsche Fläche som betyder ungefär kleinyta. Felöversättningen blev dock permanent så kleinytan kallas nu flaska även på det tyska språket.

Kleinflaskan är lokalt endast tvådimensionell men i sin helhet fyrdimensionell.

Man kan använda kleinflaskan som en termometer genom att fylla den delvis med vatten. Då temperaturen ändras kommer trycket inuti kleinflaskan öka eller minska i volym och då ändra på vattennivån i "röret". Rätt markerat och avvägt för avdunstning är detta en möjlig termometer.

Se även

• Möbiusband

Referenser

Källor

• Weisstein, Eric W. ”Klein Bottle” (på engelska). MathWorld, Wolfram Research, Inc. http://mathworld.wolfram.com/KleinBottle.html. Läst 12 januari 2010. 
• ”The Math of Non-Orientable Surfaces”. 3 december 1998. http://www.carliner-remes.com/jacob/math/project/math.htm. Läst 12 januari 2010. 

Externa länkar

• Wikimedia Commons har media som rör Kleinflaska.
  Bilder & media