So, every year our family picks names for Christmas, but this year seemed odd.  My wife pointed out that one family always just happens to randomly pick another families name.  That is the majority of the time most of one family is always trading with another, the only rule is that each family member can not trade with a member of their own family. 

I was wondering if someone could come up with a way to calculate just how random the choice actually was from the previous year or years using whatever means necessary .. graph theory came to mind.  The draw was done behind closed doors, so my wife questioned how failrly that was done, and so brought me here with the question ...
Was the name choosing really random or was it actually a fixed draw?

In our group there are total of 9 adults and 9 children, but actually the 2 youngest children swap gifts so it's really 9 adults and 7 children who can swap presents.  But I will breakdown the families less the two trading children.

Family A - 2 adults 1 child
Family B - 2 adults 2 children
Family C - 2 adults 2 children
Family D - 2 adults 2 children
Family E - 1 adult

Oh, a child can trade with another child or a parent and similarily a parent can trade with another parent or a child.  

Many everyday decisions are made using the results of coin flips and die rolls, or of similar probabilistic events. Though we would like to assume that a fair coin is being used to decide who takes the trash out or if our favorite soccer team takes possession of the ball first, it is impossible to know if the coin is weighted from a single trial.

Instead, we can perform an experiment like the one outlined in Hypothesis Testing: Doctored Coin. This is a walkthrough document for testing if a coin is fair, or if it has been doctored to favor a certain outcome. 

This hypothesis testing document comes from Maple Learn’s new Estimating collection, which contains several documents, authored by Michael Barnett, that help build an understanding of how to estimate the probability of an event occurring, even when the true probability is unknown.

One of the activities in this collection is the Likelihood Functions - Experiment document, which builds an intuitive understanding of likelihood functions. This document provides sets of observed data from binomial distributions and asks that you guess the probability of success associated with the random variable, giving feedback based on your answer. 

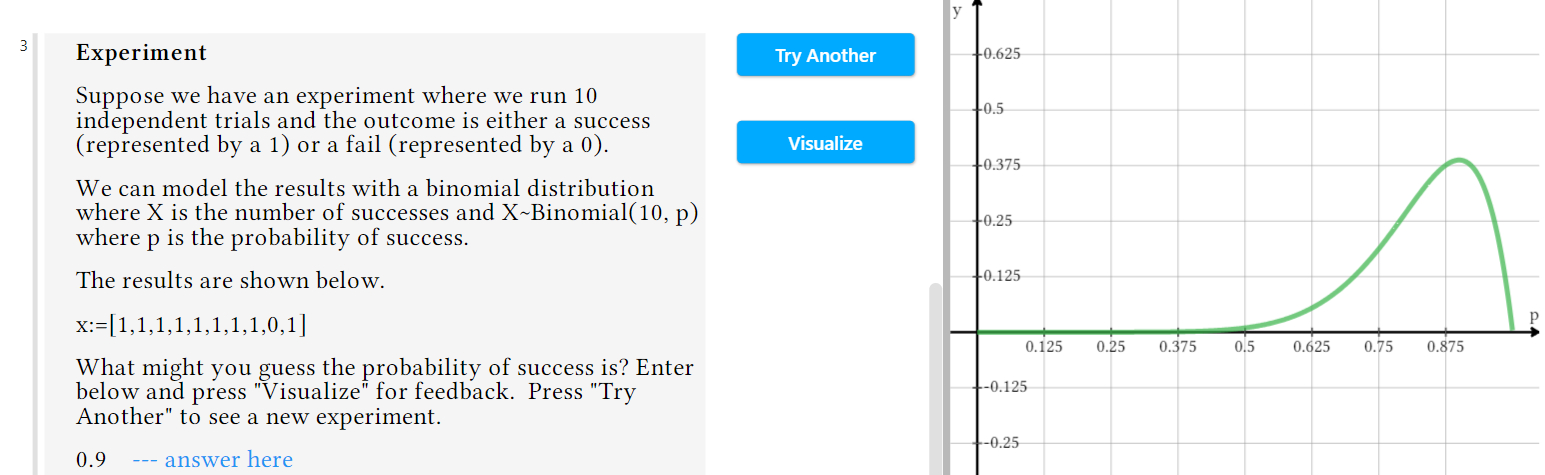
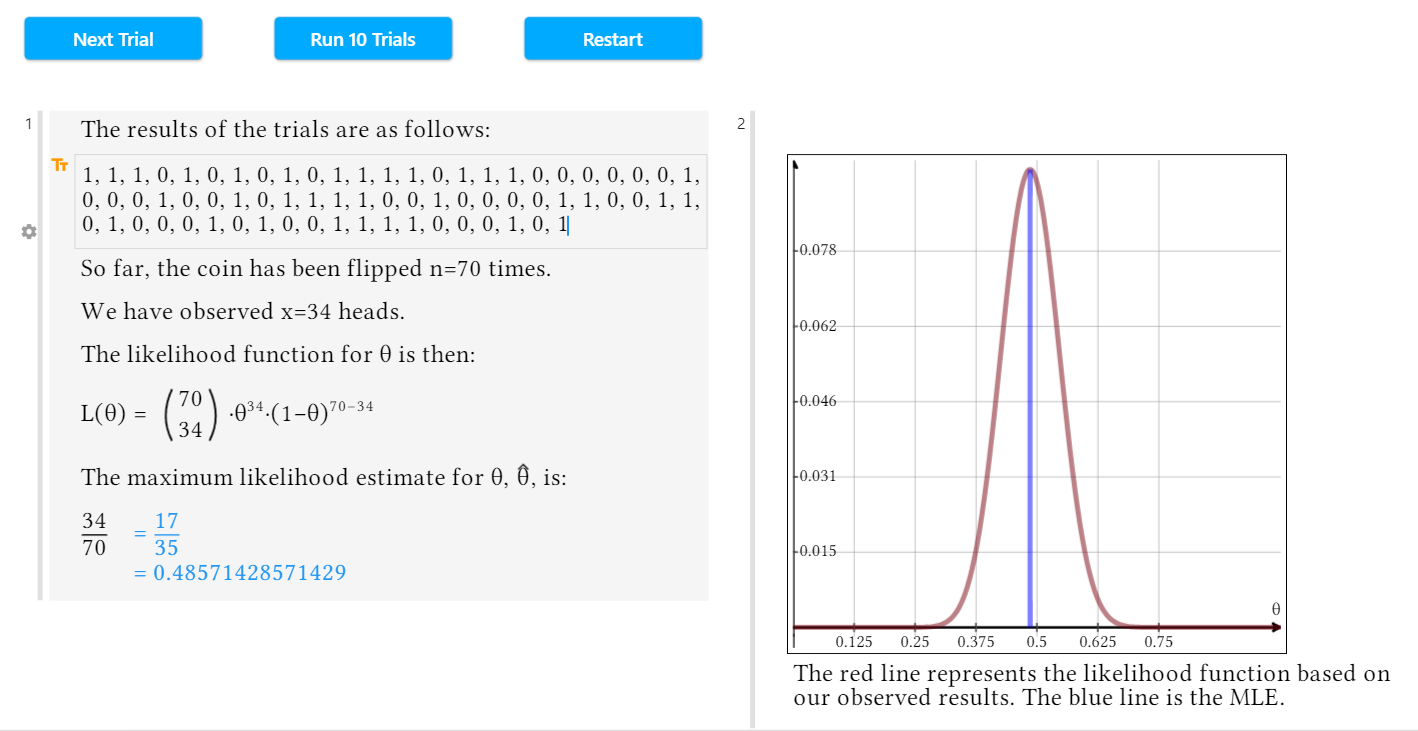
Once you’ve developed an understanding of likelihood functions, the next step in determining if a coin is biased is the Maximum Likelihood Estimate Example – Coin Flip activity. In this document, you can run as many randomized trials of coin flips as you like and see how the maximum likelihood estimate, or MLE, changes, bearing in mind that if a coin is fair, the probability of either heads or tails should be 0.5. 

Finally, in order to determine in earnest if a coin has been doctored to favor one side over the other, a hypothesis test must be performed. This is a process in which you test any data that you have against the null hypothesis that the coin is fair and determine the p-value of your data, which will help you form your conclusion.

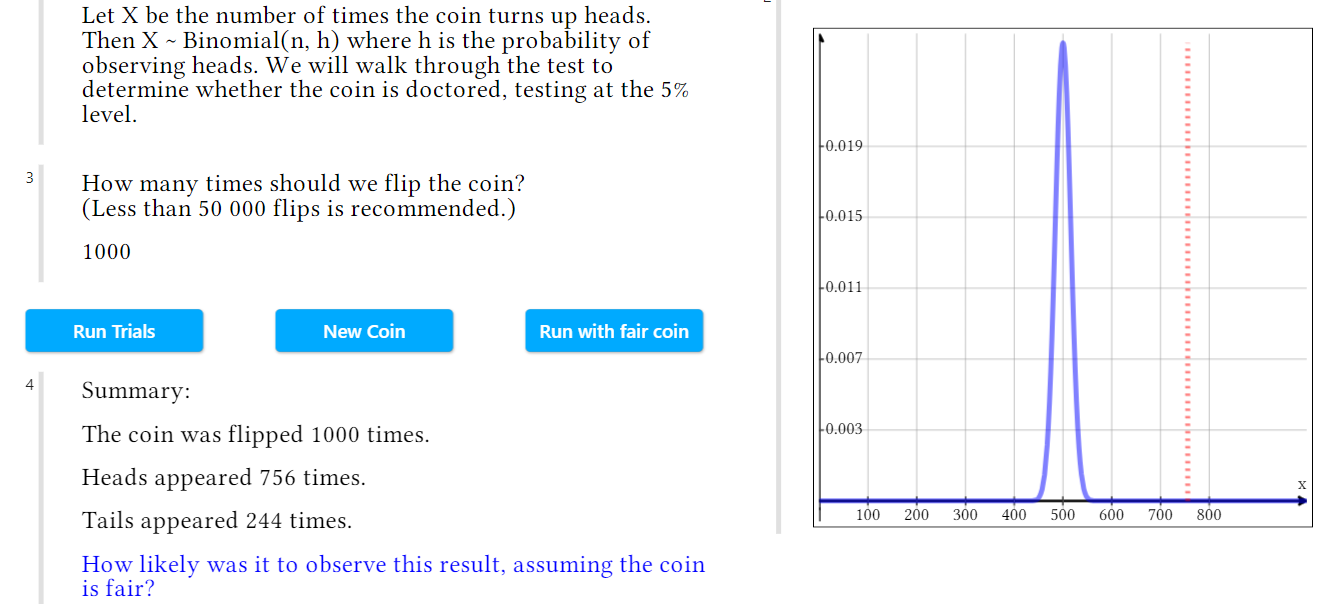
This Hypothesis Testing: Doctored Coin document is a walkthrough of a hypothesis test for a potentially biased coin. You can run a number of trials on this coin, determine the null and alternative hypotheses of your test, and find the test statistic for your data, all using your understanding of the concepts of likelihood functions and MLEs. The document will then guide you through the process of determining your p-value and what this means for your conclusion.

So if you’re having suspicions that a coin is biased or that a die is weighted, check out Maple Learn’s Estimating collection and its activities to help with your investigation!

Hi,

I wonder about how to generate the classical table of the standard normal distribution. Ideas ?

Many thanks

Probability distributions can be used to predict many things in life: how likely you are to wait more than 15 minutes at a bus stop, the probability that a certain number of credit card transactions are fraudulent, how likely it is for your favorite sports team to win at least three games in a row, and many more. 

Different situations call for different probability distributions. For instance, probability distributions can be divided into two main categories – those defined by discrete random variables and those defined by continuous random variables. Discrete probability distributions describe random variables that can only take on countable numbers of values, while continuous probability distributions are for random variables that take values from continuums, such as the real number line.

Maple Learn’s Probability Distributions section provides introductions, examples, and simulations for a variety of discrete and continuous probability distributions and how they can be used in real life. 

One of the distributions highlighted in Maple Learn’s Example Gallery is the binomial distribution. The binomial distribution is a discrete probability distribution that models the number of n Bernoulli trials that will end in a success.

This distribution is used in many real-life scenarios, including the fraudulent credit card transactions scenario mentioned earlier. All the information needed to apply this distribution is the number of trials, n, and the probability of success, p. A common usage of the binomial distribution is to find the probability that, for a recently produced batch of products, the number that are defective crosses a certain threshold; if the probability of having too many defective products is high enough, a company may decide to test each product individually rather than spot-checking, or they may decide to toss the entire batch altogether.

An interesting feature of the binomial distribution is that it can be approximated using a different type of distribution. If the number of trials, n, is large enough and the probability of success, p, is small enough, a Poisson Approximation to the Binomial Distribution can be applied to avoid potentially complex calculations. 

To see some binomial distribution calculations in action and how accurate the probabilities supplied by the distribution are, try out the Binomial Distribution Simulation document and see how the Law of Large Numbers relates to your results.