আরবি সংখ্যা
আরবি সংখ্যাগুলি দশটি সংখ্যা : ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮ এবং ৯। এই শব্দটি প্রায়শই এই অঙ্কগুলি ব্যবহার করে (দশমিকের সাথে রোমান সংখ্যার সাথে বিপরীত হলে) দশমিক সংখ্যা বোঝায়। তবে এই শব্দটি অঙ্কগুলি নিজেরাই বোঝাতে পারে যেমন বিবৃতিতে " অষ্টাল সংখ্যাগুলি আরবি সংখ্যা ব্যবহার করে লেখা হয়।"
যদিও হিন্দু – আরবি সংখ্যা পদ্ধতি (অর্থাৎ দশমিক) ভারতীয় গণিতবিদদের দ্বারা 500 খ্রিস্টাব্দের দিকে অঙ্কগুলির জন্য বেশ কয়েকটি বিভিন্ন রূপ প্রাথমিকভাবে ব্যবহৃত হয়েছিল। উত্তর আফ্রিকাতে এগুলি আরবি সংখ্যায় পরিবর্তিত হয়েছিল। এটি আলজেরীয় শহর বেজাইয়ায় ইটালিয়ান পণ্ডিত ফিবোনাচি প্রথম সংখ্যার মুখোমুখি হয়েছিলেন; ইউরোপ জুড়ে তাদের পরিচিত করার ক্ষেত্রে তাঁর কাজ অত্যন্ত গুরুত্বপূর্ণ ছিল। ইউরোপীয় বাণিজ্য, বই এবং colon পনিবেশবাদ বিশ্বজুড়ে আরবি সংখ্যাগুলি গ্রহণকে জনপ্রিয় করতে সহায়তা করেছিল। সংখ্যাগুলি লাতিন বর্ণমালার সমসাময়িক প্রসার ছাড়াই বিশ্বব্যাপী ব্যবহারের সন্ধান পেয়েছে, এমন অঞ্চলে যেখানে হিন্দু-আরবি সংখ্যাগুলির অন্যান্য রূপগুলি ব্যবহার করা হত, যেমন চীনা এবং জাপানি লেখার ক্ষেত্রে রচনার পদ্ধতিতে প্রবেশ করেছিল।
আরবি সংখ্যাটি শব্দটি পূর্ব আরবী সংখ্যাগুলির মতো আরবি রচনায় ব্যবহৃত সংখ্যার অর্থ বোঝাতে পারে। অক্সফোর্ড ইংলিশ ডিকশনারি পশ্চিমা অঙ্কগুলি উল্লেখ করার জন্য ছোট হাতের আরবি সংখ্যা ব্যবহার করে এবং পূর্বের অঙ্কগুলি উল্লেখ করার জন্য আরবি সংখ্যাগুলি বড় করে তোলে। [১]
অন্যান্য বিকল্প নাম হ'ল পশ্চিমা আরবি সংখ্যা, পশ্চিমী সংখ্যা এবং হিন্দু – আরবি সংখ্যাগুলি । ইউনিকোড কেবল অলংকৃত শব্দ সংখ্যা ব্যবহার করে। [২]
ইতিহাস
উৎপত্তি

দশমিক হিন্দু – আরবি সংখ্যা ব্যবস্থার ভারতে প্রায় 700 খৃষ্টাব্দে বিকাশ ঘটেছিল। [৫] বিকাশটি ধীরে ধীরে ছিল এবং কয়েক শতাব্দী জুড়ে বিস্তৃত ছিল, তবে সম্ভবত নির্ধারিত পদক্ষেপটি ব্রহ্মগুপ্তের zero২৮ সালে একটি সংখ্যা হিসাবে শূন্যের সূচনা দ্বারা সরবরাহ করা হয়েছিল।
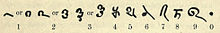
সংখ্যা সিস্টেম থেকে পরিচিতি লাভ করেন বাগদাদ আদালতে, যেখানে যেমন mathematicians ফার্সি আল-খোয়ারিজমি, যার বই হিন্দু সংখ্যা (সঙ্গে ক্যালকুলেশন উপর আরবি: الجمع والتفريق بالحساب الهندي আল-জামা ওয়াল-তাফরাক বিল-ইসিব আল-হিন্দী ) আরবী ভাষায় প্রায় ৮২২ টি রচিত হয়েছিল এবং তারপরে আরব গণিতবিদ আল-কিন্দি লিখেছিলেন, যিনি চারটি খন্ড লিখেছিলেন, ভারতীয় সংখ্যাগুলির ব্যবহার সম্পর্কে ( আরবি: كتاب في استعمال الأعداد الهندية 830 সালের দিকে কিতাব ফ ইসতিমাল আল-'আদাদ আল-হিন্দিয়া'য়। তাদের কাজটি মূলত মধ্য প্রাচ্য এবং পাশ্চাত্যে ভারতীয় সংখ্যা ব্যবস্থার বিস্তারের জন্য দায়ী ছিল। [৬]
মধ্য-পূর্বাঞ্চলের গণিতবিদগণ দশমিক সংখ্যাটি প্রসারিত করে ভগ্নাংশকে অন্তর্ভুক্ত করেছিলেন, যেমনটি 952-953 -এ আরব গণিতবিদ আবু-হাসান আল- উকলিদিসীর একটি গ্রন্থে লিপিবদ্ধ রয়েছে। দশমিক পয়েন্ট স্বরলিপি চালু হয়েছিল[কখন?] সিন্ধ ইবনে আলী রচিত, যিনি আরবি সংখ্যার উপর প্রথম গ্রন্থটিও লিখেছিলেন।
আরবি সংখ্যা চিহ্নগুলির উত্স
আল-বিরুনির মতে, ভারতে বহু ধরনের সংখ্যা ব্যবহৃত হয়েছিল এবং "আরবরা তাদের মধ্যে এমনটি বেছে নিয়েছিল যা তাদের কাছে সবচেয়ে কার্যকর বলে মনে হয়েছিল"।[তথ্যসূত্র প্রয়োজন] আল-নাসাভি একাদশ শতাব্দীর গোড়ার দিকে লিখেছিলেন যে গণিতবিদগণ অঙ্কের আকারে একমত নন, তবে তাদের বেশিরভাগই নিজেকে পূর্বের আরবি সংখ্যা হিসাবে পরিচিত ফর্মগুলির সাথে প্রশিক্ষণ দিতে রাজি হয়েছিল। [৭] মিশর থেকে 873–874 সালে প্রাপ্ত লিখিত সংখ্যাগুলির প্রাচীনতম নমুনাগুলিতে "2" সংখ্যাটির তিনটি রূপ এবং "3" সংখ্যার দুটি ফর্ম দেখা যায়, এবং এই প্রকরণগুলি পূর্বের হিসাবে পরিচিত হয়ে ওঠার মধ্যকার বিভেদকে নির্দেশ করে আরবি সংখ্যা এবং (পশ্চিমা) আরবি সংখ্যাগুলি। [৮]
প্রতীকগুলির পশ্চিম আরবি রূপগুলি মাগরেব এবং আল-আন্দালাসে ব্যবহৃত হতে শুরু করে, যা আধুনিক আরবি সংখ্যাগুলির সরাসরি পূর্বপুরুষ। [৯]
গণনাগুলি মূলত একটি ডাস্ট বোর্ড ( টখত, লাতিন: তাবুলা ) ব্যবহার করে সম্পাদিত হয় যা স্টাইলাস সহ চিহ্নগুলি লিখতে এবং গণনার অংশ হিসাবে মুছে ফেলার সাথে জড়িত। আল-উকালিদিসি তখন কালি ও কাগজ দিয়ে "বোর্ড এবং ভাঙা ছাড়াই" (দ্বি-গায়র তাকত ওয়া-ল-মাউ বাল বাল দ্বি-ওয়া ক্বিরিস ) দিয়ে গণনার একটি পদ্ধতি আবিষ্কার করেছিলেন। [৮] সঙ্গে হিসাব যেহেতু হিন্দু হিসাব ḥisāb আল-হিন্দি পূর্বাঞ্চলে বলা হত, এটা পশ্চিমে (আক্ষরিক মধ্যে ḥisāb আল-ghubār বলা হত, ": ধুলো বোর্ড ব্যবহারের পাশাপাশি পরিভাষা একটি বিকিরণ চালু হয়েছে বলে মনে হচ্ছে ধূলা ")। [৮] অঙ্কগুলিকে নিজেদের পশ্চিমে আশ্কাল আল-ঘোবার (ইবনে আল-ইয়াসমিনের ধূলিকণা) বা ক্বালাম আল-ঘোবার (ধূলিকণা) বলা হত। [৮] পরিভাষাটির বিবর্তনের ফলে কিছু পণ্ডিতকে এই প্রস্তাব দেওয়া হয়েছিল যে তথাকথিত "ঘুবরের সংখ্যা "গুলিতে পাশ্চাত্য আরবি সংখ্যাগুলির একটি পৃথক উত্স রয়েছে তবে উপলভ্য প্রমাণগুলি কোনও পৃথক উত্সের ইঙ্গিত দেয় না। [১০]
ওউপেকও প্রস্তাব দিয়েছেন যে আলেকজান্দ্রিয়ার মধ্য দিয়ে প্রাপ্ত মুরসের আগমনের পূর্বে স্পেনে পশ্চিমা আরবি সংখ্যাগুলি ইতিমধ্যে ব্যবহৃত হয়েছিল, তবে এই তত্ত্বটি পণ্ডিতদের দ্বারা গৃহীত হয়নি। [১১]
কিছু জনপ্রিয় পৌরাণিক কল্পকাহিনী যুক্তি দেয় যে এই চিহ্নগুলির মূল ফর্মগুলি তাদের সংখ্যা অনুসারে যে সংখ্যাগুলিকে ধারণ করেছিল, তার মধ্য দিয়ে তাদের সংখ্যাগত মান নির্দেশ করে, তবে এরূপ কোনও উত্সের প্রমাণ নেই। [১২]
ইউরোপে দত্তক




ইউরোপ এবং আমেরিকাতে ডিজিটগুলি বেশি বেশি "আরবি সংখ্যা" হিসাবে পরিচিত হওয়ার কারণ হ'ল দশম শতাব্দীতে উত্তর আফ্রিকার আরবি-স্পিকাররা ইউরোপের সাথে পরিচয় করিয়েছিল, যারা তখন লিবিয়া থেকে মরক্কোতে অঙ্কগুলি ব্যবহার করছিল। আরবরা অন্যান্য অঞ্চলে পূর্ব আরবি সংখ্যাগুলি (٠١٢٣٤٥٦٧٨٩) ব্যবহার করছিল।
৮২২ খ্রিস্টাব্দে আল-খুয়ারিজমি আরবিতে একটি গ্রন্থ রচনা করেছিলেন, হিন্দু সংখ্যার সাথে গণনার উপর, [১৩] যা কেবল দ্বাদশ শতাব্দীর লাতিন অনুবাদ, আলগোরিটমি দে নুমেরো ইন্দোরাম হিসাবে টিকে আছে । [১৪] [১৫] Algoritmi, লেখক নাম অনুবাদক এর প্রতিদান, শব্দ বৃদ্ধি দিয়েছেন অ্যালগরিদম । [১৬]
পাশ্চাত্যে অঙ্কগুলির প্রথম উল্লেখগুলি 976 এর কোডেক্স ভিজিলানাসে [১৭]
980s থেকে, এর Gerbert আরিলেক (পরবর্তীকালে, পোপ সিলভেস্টার দ্বিতীয় ) তার অবস্থানে ইউরোপে সংখ্যাসমূহ বিস্তারের জ্ঞান করতেন। গারবার্ট যৌবনে বার্সেলোনায় পড়াশোনা করেছিলেন। তিনি বিষয়ে গাণিতিক গ্রন্থ অনুরোধ করেছেন তাদের পরিচিত ছিল জ্যোতির্বিজ্ঞানের থেকে বার্সেলোনার Lupitus পর ফ্রান্সে ফিরে এসেছে।[তথ্যসূত্র প্রয়োজন]
লিওনার্দো ফিবানচি ( পিসা লিওনার্দো ), জন্ম একজন গণিতবিদ পিসা প্রজাতন্ত্র যারা পড়াশোনা করেছে মধ্যে Bejaia (মোমবাতি), আলজেরিয়া, তার 1202 বই সাথে ইউরোপে ভারতীয় সংখ্যা সিস্টেম উন্নীত লাইবার Abaci :
আমার বাবা, যিনি তার দেশ পিসান ব্যবসায়ীদের সেখানে অভিনয় করার জন্য বুগিয়ার প্রথা অনুসারে পাবলিক নোটারি হিসাবে নিযুক্ত ছিলেন, যখন দায়িত্বে ছিলেন, তখন আমি যখন ছোট ছিলাম তখনই তিনি আমাকে তাঁর কাছে ডেকেছিলেন এবং উপযোগিতার দিকে নজর রেখেছিলেন এবং ভবিষ্যতের সুবিধার্থে, আমাকে সেখানে থাকতে এবং অ্যাকাউন্টিং স্কুলে নির্দেশনা গ্রহণ করার ইচ্ছা করেছিল। সেখানে যখন আমি উল্লেখযোগ্য শিক্ষার মাধ্যমে ভারতীয়দের নয়টি প্রতীকের শিল্পের সাথে পরিচয় করিয়েছিলাম, তখন শিল্পের জ্ঞান খুব শীঘ্রই আমাকে অন্য সকলের থেকে সন্তুষ্ট করেছিল এবং আমি এটি বুঝতে পারি।
অঙ্কগুলির ইউরোপীয় গ্রহণযোগ্যতা মুদ্রণযন্ত্রের আবিষ্কার দ্বারা ত্বরান্বিত হয়েছিল এবং 15 তম শতাব্দীতে এগুলি ব্যাপকভাবে পরিচিত হয়ে ওঠে। ব্রিটেনে তাদের ব্যবহারের প্রারম্ভিক প্রমাণগুলির মধ্যে রয়েছে: ১৩ 139 hour সাল থেকে সমতুল্য এক ঘণ্টার চতুর্থাংশ [১৮] ইংল্যান্ডে, সাসেক্সের হিথফিল্ড চার্চের টাওয়ারে একটি 1445 শিলালিপি; বার্কশায়ার ব্রা চার্চের কাঠের লীচ-গেটে একটি 1448 শিলালিপি; এবং পিডলেট্রেন্থাইড গির্জার, ডরসেটের বেলফ্রি দরজার উপর একটি 1487 শিলালিপি; এবং স্কটল্যান্ডে এলগিন ক্যাথেড্রালের হান্টির প্রথম আর্লের সমাধিতে একটি 1470 শিলালিপি রয়েছে। (আরও উদাহরণের জন্য জিএফ হিল, ইউরোপের আরবি সংখ্যার বিকাশ দেখুন। ) মধ্য ইউরোপে, হাঙ্গেরির বাদশাহ লাডিসালাস মরণোত্তর, আরবি সংখ্যার ব্যবহার শুরু করেছিলেন, যা প্রথমবারের মতো ১৪৫6 এর রাজকীয় নথিতে প্রকাশিত হয়েছে। [১৯] ষোড়শ শতাব্দীর মধ্যভাগে, তারা ইউরোপের বেশিরভাগ ক্ষেত্রে প্রচলিত ছিল। [২০] রোমান সংখ্যাগুলি বেশিরভাগ এলো ডোমিনি বছরের স্বরলিপি এবং ক্লকফেসে সংখ্যার জন্য ব্যবহৃত হয়।
১ Europe৫7 সালে প্রকাশিত হিস্টোয়ার দে লা ম্যাথাম্যাটিক -এ ফরাসী পণ্ডিত জাঁ-এতিয়েন মন্টুচলার তৈরি একটি টেবিলের প্রথম দিকে ইউরোপের অঙ্কগুলির বিবর্তন এখানে দেখানো হয়েছে:
আজও রোমান সংখ্যাগুলি তালিকা অনুসারে (বর্ণানুক্রমিক গণনার বিকল্প হিসাবে), অনুক্রমিক খণ্ডের জন্য, একই প্রথম নামগুলির সাথে রাজা বা পরিবারের সদস্যদের পৃথক করতে এবং বইগুলিতে প্রিফেটরি উপাদানগুলিতে পৃষ্ঠাগুলির সংখ্যা পৃষ্ঠাতে পৃথক করার জন্য ব্যবহৃত হয় পাশাপাশি ক্লকফেসে।
রাশিয়ায় আরবি সংখ্যা গ্রহণ
সিরিলিক সংখ্যাগুলি দক্ষিণ ও পূর্ব স্লাভিক লোকেরা ব্যবহৃত সিরিলিক বর্ণমালা থেকে প্রাপ্ত একটি সংখ্যক পদ্ধতি ছিল। 18 শতকের গোড়ার দিকে রাশিয়ায় এই সিস্টেমটি ব্যবহৃত হয়েছিল যখন পিটার গ্রেট এটিকে আরবি সংখ্যার সাথে প্রতিস্থাপন করেছিলেন।
চীনে আরবি সংখ্যা গ্রহণ

মুসলিম হুই জনগণের দ্বারা ইউয়ান রাজবংশের (1271681368) সময় চীনে অবস্থানগত স্বরলিপি প্রবর্তিত হয়েছিল। 17 শতকের গোড়ার দিকে, ইউরোপীয় ধাঁচের আরবি সংখ্যা স্প্যানিশ এবং পর্তুগিজ জেসুইট দ্বারা প্রবর্তিত হয়েছিল by [২১] [২২] [২৩]
এনকোডিং
দশটি আরবি সংখ্যাগুলি মোর্স কোডের মতো বৈদ্যুতিন, রেডিও এবং ডিজিটাল যোগাযোগের জন্য ডিজাইন করা কার্যত প্রতিটি অক্ষর সেটগুলিতে এনকোড থাকে।
তারা 0x30 থেকে 0x39 পজিশনে ASCII এ এনকোডেড রয়েছে। নিম্ন 4 টি বাইনারি বিটগুলিতে মাস্কিং (বা শেষ হেক্সাডেসিমাল অঙ্কটি গ্রহণ করা) ডিজিটের মান দেয়, প্রাথমিক কম্পিউটারগুলিতে পাঠ্যকে সংখ্যায় রূপান্তরিত করতে একটি দুর্দান্ত সহায়তা। এই অবস্থানগুলি ইউনিকোডে উত্তরাধিকারসূত্রে প্রাপ্ত হয়েছিল। [২৪] EBCDIC বিভিন্ন মান ব্যবহার করেছে তবে এর চেয়ে কম 4 টি বিট ডিজিট মানের সাথেও রয়েছে।
| বাইনারি | অক্টাল | দশমিক | হেক্স | গ্লাইফ | ইউনিকোড | EBCDIC (হেক্স) |
|---|---|---|---|---|---|---|
| 00110000 | 060 | 48 | 30 | 0 | U + 0030 ডিজিট জিরো | F0 |
| 00110001 | 061 | 49 | 31 | ঘ | U + 0031 ডিজিট এক | F1 |
| 00110010 | 062 | 50 | 32 | ঘ | ইউ + 0032 ডিজিট দুটি | F2 |
| 00110011 | 063 | 51 | 33 | ঘ | U + 0033 তিনটি ডিজিট করুন | F3 |
| 00110100 | 064 | 52 | 34 | ঘ | U + 0034 ডিজিট চার | F4 |
| 00110101 | 065 | 53 | 35 | ৫ | U + 0035 পাঁচটি ডিজিট | F5 |
| 00110110 | 066 | 54 | 36 | । | U + 0036 ডিজিট সিক্স | F6 |
| 00110111 | 067 | 55 | 37 | 7 | U + 0037 ডিজিট সেভেন | F7 |
| 00111000 | 070 | 56 | 38 | 8 | U + 0038 ডিজিট আট | F8 |
| 00111001 | 071 | 57 | 39 | 9 | ইউ + 0039 ডিজিট নাইন | F9 |
তথ্যসূত্র
- ↑ "Arabic", Oxford English Dictionary, 2nd edition
- ↑ Official Unicode Consortium code chart
- ↑ Smith, David Eugene; Karpinski, Louis Charles (১৯১১)। The Hindu-Arabic numerals। Boston, London, Ginn and Company। পৃষ্ঠা 52।
- ↑ For a modern image
- ↑ O'Connor, J. J. and E. F. Robertson. 2000. Indian Numerals ওয়েব্যাক মেশিনে আর্কাইভকৃত ২৯ সেপ্টেম্বর ২০০৭ তারিখে, MacTutor History of Mathematics Archive, School of Mathematics and Statistics, University of St. Andrews, Scotland.
- ↑ The MacTutor History of Mathematics archive
- ↑ Kunitzsch, The Transmission of Hindu-Arabic Numerals Reconsidered 2003: "Les personnes qui se sont occupées de la science du calcul n'ont pas été d'accord sur une partie des formes de ces neuf signes; mais la plupart d'entre elles sont convenues de les former comme il suit."
- ↑ ক খ গ ঘ Kunitzsch, The Transmission of Hindu-Arabic Numerals Reconsidered 2003।
- ↑ Kunitzsch, The Transmission of Hindu-Arabic Numerals Reconsidered 2003: "While specimens of Western Arabic numerals from the early period—the tenth to thirteenth centuries—are still not available, we know at least that Hindu reckoning (called ḥisāb al-ghubār) was known in the West from the tenth century onward..."
- ↑ Kunitzsch, The Transmission of Hindu-Arabic Numerals Reconsidered 2003: 'I should think that, therefore, it is no longer justified for us to call the Western Arabic forms of the Hindu-Arabic numerals "ghubār numerals." Rather we should speak of the Eastern and the Western Arabic forms of the nine numerals.'
- ↑ Kunitzsch, The Transmission of Hindu-Arabic Numerals Reconsidered 2003: "Since edition of and research on the Pseudo-Boethius[41] we now know that the texts running under his name and carrying Arabic numerals date from the eleventh century. Thus the assumed way of transmission from Alexandria to Spain is impossible and this theory can no longer be taken as serious."
- ↑ Ifrah, Georges (১৯৯৮)। The universal history of numbers: from prehistory to the invention of the computer; translated from the French by David Bellos। Harvill Press। পৃষ্ঠা 356–357। আইএসবিএন 9781860463242।
- ↑ Philosophy Of Mathematics Francis, John – 2008 – Page 38
- ↑ The Ellipse: A Historical and Mathematical Journey Arthur Mazer – 2011
- ↑ "al-Khwarizmi - Muslim mathematician"।
- ↑ Models of Computation: An Introduction to Computability Theory – Page 1 Maribel Fernández – 2009
- ↑ "MATHORIGINS.COM_V"। www.mathorigins.com।
- ↑ "14th century timepiece unearthed in Qld farm shed"। ABC News।
- ↑ Erdélyi: Magyar művelődéstörténet 1-2. kötet. Kolozsvár, 1913, 1918
- ↑ Mathforum.org
- ↑ Encyclopaedia of the history of science, technology, and medicine in non-western cultures। Springer। ১৯৯৭। পৃষ্ঠা 198। আইএসবিএন 978-0-7923-4066-9।
- ↑ Meuleman, Johan H. (২০০২)। Islam in the era of globalization: Muslim attitudes towards modernity and identity। Psychology Press। পৃষ্ঠা 272। আইএসবিএন 978-0-7007-1691-3।
- ↑ Peng Yoke Ho (২০০০)। Li, Qi and Shu: An Introduction to Science and Civilization in China। Courier Dover Publications। পৃষ্ঠা 106। আইএসবিএন 978-0-486-41445-4।
- ↑ https://www.unicode.org/charts/PDF/U0000.pdf
বহিঃসংযোগ
- হিন্দু আরবি এবং ditionতিহ্যবাহী চীনা পাটিগণিতের বিকাশ
- গণনা পদ্ধতি এবং সংখ্যাগুলির ইতিহাস । 11 ডিসেম্বর 2005-এ পুনরুদ্ধার করা হয়েছে।
- নম্বর বিবর্তন ওয়েব্যাক মেশিনে আর্কাইভকৃত ২২ মার্চ ২০১২ তারিখে । 16 এপ্রিল 2005।
- ও'কনোর, জেজে এবং রবার্টসন, ইএফ ভারতীয় সংখ্যাগুলি ওয়েব্যাক মেশিনে আর্কাইভকৃত ৬ জুলাই ২০১৫ তারিখে । নভেম্বর 2000।
- সংখ্যার ইতিহাস
- আরবি সংখ্যা
- হিন্দু-আরবি সংখ্যা
- সংখ্যা এবং সংখ্যাগুলির ইতিহাস এবং কৌতূহল
- Gerbert d'আরিলেক এর হিন্দু-আরবি সংখ্যাসূচক প্রথম ব্যবহার ওয়েব্যাক মেশিনে আর্কাইভকৃত ১৩ জুলাই ২০১৫ তারিখে এ কনভার্জেন্স ওয়েব্যাক মেশিনে আর্কাইভকৃত ৮ আগস্ট ২০১৩ তারিখে
