Constructible polygon: Difference between revisions
→Gallery: I couldn't get the 257-gon animation to play in reduced mode, for some reason. |
Undid revision 1221232636 by EuclidIncarnated (talk) Making the definition of a Fermat prime accessible only through a hyperlink, and removing the brief gloss here, violates WP:TECHNICAL |
||
| (157 intermediate revisions by 70 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Regular polygon that can be constructed with compass and straightedge}} |
|||
[[Image:Pentagon construct.gif|thumb|Construction of a regular pentagon]] |
[[Image:Pentagon construct.gif|thumb|Construction of a regular pentagon]] |
||
In mathematics, a '''constructible polygon''' is a [[regular polygon]] that can be [[Compass and straightedge constructions|constructed with compass and straightedge]]. For example, a regular [[pentagon]] is constructible with compass and straightedge while a regular [[heptagon]] is not. |
In [[mathematics]], a '''constructible polygon''' is a [[regular polygon]] that can be [[Compass and straightedge constructions|constructed with compass and straightedge]]. For example, a regular [[pentagon]] is constructible with compass and straightedge while a regular [[heptagon]] is not. There are infinitely many constructible polygons, but only 31 with an [[odd number]] of sides are known. |
||
==Conditions for constructibility== |
==Conditions for constructibility== |
||
[[File:Constructible polygon set.svg|thumb|300px|Number of sides of known constructible polygons having up to 1000 sides (bold) or odd side count (red)]] |
|||
[[File:HeptadecagonConstructionAni.gif|thumb |
[[File:HeptadecagonConstructionAni.gif|thumb|Construction of the regular {{nowrap|17-gon}}]] |
||
Some regular polygons are easy to construct with compass and straightedge; others are not. This led to the question being posed: is it possible to construct ''all'' regular ''n''-gons with compass and straightedge? If not, which ''n''-gons are constructible and which are not? |
|||
Some regular polygons are easy to construct with compass and straightedge; others are not. The [[Greek mathematics|ancient Greek mathematicians]] knew how to construct a regular polygon with 3, 4, or 5 sides,<ref name=Bold/>{{rp|p. xi}} and they knew how to construct a regular polygon with double the number of sides of a given regular polygon.<ref name=Bold>Bold, Benjamin. ''Famous Problems of Geometry and How to Solve Them'', Dover Publications, 1982 (orig. 1969).</ref>{{rp|pp. 49–50}} This led to the question being posed: is it possible to construct ''all'' regular polygons with compass and straightedge? If not, which ''n''-gons (that is, [[polygon]]s with ''n'' edges) are constructible and which are not? |
|||
[[Carl Friedrich Gauss]] proved the constructibility of the regular [[heptadecagon|17-gon]] in 1796. Five years later, he developed the theory of [[Gaussian period]]s in his ''[[Disquisitiones Arithmeticae]]''. This theory allowed him to formulate a [[sufficient condition]] for the constructibility of regular polygons: |
{{anchor|1=Gauss–Wantzel theorem}}[[Carl Friedrich Gauss]] proved the constructibility of the regular [[heptadecagon|17-gon]] in 1796. Five years later, he developed the theory of [[Gaussian period]]s in his ''[[Disquisitiones Arithmeticae]]''. This theory allowed him to formulate a [[sufficient condition]] for the constructibility of regular polygons. Gauss stated without proof that this condition was also [[necessary condition|necessary]],<ref>{{cite book |last1=Gauss |first1=Carl Friedrich |title=Disquisitiones arithmeticae |date=1966 |publisher=Yale University Press |location=New Haven and London |pages=458–460 |url=https://archive.org/details/disquisitionesar0000carl/ |access-date=25 January 2023}}</ref> but never published his proof. |
||
:A regular ''n''-gon can be constructed with compass and straightedge if ''n'' is the product of a power of 2 and any number of distinct [[Fermat prime]]s. |
A full proof of necessity was given by [[Pierre Wantzel]] in 1837. The result is known as the '''Gauss–Wantzel theorem''': A regular ''n''-gon can be constructed with compass and straightedge [[if and only if]] ''n'' is the product of a [[power of 2]] and any number of distinct [[Fermat prime]]s. Here, a power of 2 is a number of the form <math>2^m</math>, where ''m'' ≥ 0 is an integer. A Fermat prime is a [[prime number]] of the form <math>2^{(2^m)} + 1</math>, where ''m'' ≥ 0 is an integer. The number of Fermat primes involved can be 0, in which case ''n'' is a power of 2. |
||
In order to reduce a [[geometry|geometric]] problem to a problem of pure [[number theory]], the proof uses the fact that a regular ''n''-gon is constructible if and only if the [[cosine]] <math>\cos(2\pi/n)</math> is a [[constructible number]]—that is, can be written in terms of the four basic arithmetic operations and the extraction of [[square root]]s. Equivalently, a regular ''n''-gon is constructible if any [[root of a function|root]] of the ''n''th [[cyclotomic polynomial]] is constructible. |
|||
Gauss stated without proof that this condition was also [[necessary condition|necessary]], but never published his proof. A full proof of necessity was given by [[Pierre Wantzel]] in 1837. The result is known as the '''Gauss–Wantzel theorem'''. |
|||
===Detailed results by Gauss' theory=== |
===Detailed results by Gauss's theory=== |
||
Restating the Gauss–Wantzel theorem: |
|||
| ⚫ | |||
:'' |
:A regular ''n''-gon is constructible with straightedge and compass if and only if ''n'' = 2<sup>''k''</sup>''p''<sub>1</sub>''p''<sub>2</sub>...''p''<sub>''t''</sub> where ''k'' and ''t'' are non-negative [[integer]]s, and the ''p''<sub>''i''</sub>'s (when ''t'' > 0) are distinct Fermat primes. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
:'' |
:''F''<sub>0</sub> = 3, ''F''<sub>1</sub> = 5, ''F''<sub>2</sub> = 17, ''F''<sub>3</sub> = 257, and ''F''<sub>4</sub> = 65537 {{OEIS|id=A019434}}. |
||
| ⚫ | |||
Since there are 31 nonempty subsets of the five known Fermat primes, there are 31 known constructible polygons with an odd number of sides. |
|||
:''n'' = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, … {{OEIS|id=A004169}}. |
|||
| ⚫ | |||
| ⚫ | |||
:''n'' = [[Equilateral triangle|3]], [[Square|4]], [[Pentagon|5]], [[Hexagon|6]], [[Octagon|8]], [[Decagon|10]], [[Dodecagon|12]], [[Pentadecagon|15]], [[Hexadecagon|16]], [[Heptadecagon|17]], [[Icosagon|20]], [[Icositetragon|24]], [[Triacontagon|30]], [[Triacontadigon|32]], [[Triacontatetragon|34]], [[Tetracontagon|40]], [[Tetracontaoctagon|48]], 51, [[Hexacontagon|60]], [[Hexacontatetragon|64]], 68, [[Octacontagon|80]], 85, [[Enneacontahexagon|96]], 102, [[120-gon|120]], 128, 136, 160, 170, 192, 204, 240, 255, 256, [[257-gon|257]], 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, ... {{OEIS|id=A003401}}, |
|||
| ⚫ | |||
:''n'' = [[Heptagon|7]], [[Enneagon|9]], [[Hendecagon|11]], [[Tridecagon|13]], [[Tetradecagon|14]], [[Octadecagon|18]], [[Enneadecagon|19]], [[Icosihenagon|21]], [[Icosidigon|22]], [[Icositrigon|23]], 25, [[Icosihexagon|26]], 27, [[Icosioctagon|28]], 29, 31, 33, 35, 36, 37, 38, 39, 41, [[Tetracontadigon|42]], 43, 44, 45, 46, 47, 49, [[Pentacontagon|50]], 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 65, 66, 67, 69, [[Heptacontagon|70]], 71, 72, 73, 74, 75, 76, 77, 78, 79, 81, 82, 83, 84, 86, 87, 88, 89, [[Enneacontagon|90]], 91, 92, 93, 94, 95, 97, 98, 99, [[Hectogon|100]], 101, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122, 123, 124, 125, 126, 127, ... {{OEIS|id=A004169}}. |
|||
===Connection to Pascal's triangle=== |
===Connection to Pascal's triangle=== |
||
Since there are 5 known Fermat primes, we know of 31 numbers that are products of distinct Fermat primes, and hence 31 constructible odd-sided regular polygons. These are 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, [[65537-gon|65537]], 196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295 {{OEIS|id=A045544}}. As [[John Conway]] commented in ''The Book of Numbers'', these numbers, when written in [[binary number|binary]], are equal to the first 32 rows of the [[Modular arithmetic|modulo]]-2 [[Pascal's triangle]], minus the top row, which corresponds to a [[monogon]]. (Because of this, the 1s in such a list form an approximation to the [[Sierpiński triangle]].) This pattern breaks down after this, as the next Fermat number is composite (4294967297 = 641 × 6700417), so the following rows do not correspond to constructible polygons. It is unknown whether any more Fermat primes exist, and it is therefore unknown how many odd-sided constructible regular polygons exist. In general, if there are ''q'' Fermat primes, then there are 2<sup>''q''</sup>−1 {{nowrap|odd-sided}} regular constructible polygons. |
|||
==General theory== |
==General theory== |
||
In the light of later work on [[Galois theory]], the principles of these proofs have been clarified. It is straightforward to show from [[analytic geometry]] that constructible lengths must come from base lengths by the solution of some sequence of [[quadratic equation]]s. |
In the light of later work on [[Galois theory]], the principles of these proofs have been clarified. It is straightforward to show from [[analytic geometry]] that constructible lengths must come from base lengths by the solution of some sequence of [[quadratic equation]]s.<ref>{{citation |
||
| last = Cox | first = David A. | authorlink = David A. Cox |
|||
| contribution = Theorem 10.1.6 |
|||
| doi = 10.1002/9781118218457 |
|||
| edition = 2nd |
|||
| isbn = 978-1-118-07205-9 |
|||
| page = 259 |
|||
| publisher = John Wiley & Sons |
|||
| series = Pure and Applied Mathematics |
|||
| title = Galois Theory |
|||
| year = 2012}}.</ref> In terms of [[field theory (mathematics)|field theory]], such lengths must be contained in a [[field extension]] generated by a tower of [[quadratic extension]]s. It follows that a field generated by constructions will always have [[degree of a field extension|degree]] over the base field that is a power of two. |
|||
In the specific case of a regular ''n''-gon, the question reduces to the question of constructing a length |
In the specific case of a regular ''n''-gon, the question reduces to the question of [[constructible number|constructing a length]] |
||
:cos |
:cos {{sfrac|2{{pi}}|''n''}} , |
||
This number lies in the ''n''-th [[cyclotomic field]] — and in fact in its real subfield, which is a [[totally real field]] and a [[rational |
which is a [[trigonometric number]] and hence an [[algebraic number]]. This number lies in the ''n''-th [[cyclotomic field]] — and in fact in its [[real number|real]] [[field extension|subfield]], which is a [[Totally real number field|totally real field]] and a [[rational number|rational]] [[vector space]] of [[Hamel dimension|dimension]] |
||
:½ |
:½  |
||
where |
where |
||
As for the construction of Gauss, when the Galois group is 2-group it follows that it has a sequence of |
As for the construction of Gauss, when the [[Galois group]] is a 2-group it follows that it has a sequence of [[subgroup]]s of orders |
||
:1, 2, 4, 8, ... |
:1, 2, 4, 8, ... |
||
that are nested, each in the next (a [[composition series]], in [[group theory]] |
that are nested, each in the next (a [[composition series]], in [[group theory]] terminology), something simple to prove by [[mathematical induction|induction]] in this case of an [[abelian group]]. Therefore, there are subfields nested inside the cyclotomic field, each of degree 2 over the one before. Generators for each such field can be written down by [[Gaussian period]] theory. For example, for [[heptadecagon|''n'' = 17]] there is a period that is a sum of eight [[roots of unity]], one that is a sum of four roots of unity, and one that is the sum of two, which is |
||
:cos {{sfrac|2{{pi}}|17}} . |
|||
:''cos''(2 |
|||
Each of those is a root of a quadratic equation in terms of the one before. Moreover these equations have real rather than |
Each of those is a root of a [[quadratic equation]] in terms of the one before. Moreover, these equations have [[real number|real]] rather than [[complex number|complex]] roots, so in principle can be solved by geometric construction: this is because the work all goes on inside a totally real field. |
||
In this way the result of Gauss can be understood in current terms; for actual calculation of the equations to be solved, the periods can be squared and compared with the 'lower' periods, in a quite feasible algorithm. |
In this way the result of Gauss can be understood in current terms; for actual calculation of the equations to be solved, the periods can be squared and compared with the 'lower' periods, in a quite feasible algorithm. |
||
| Line 55: | Line 74: | ||
== Compass and straightedge constructions == |
== Compass and straightedge constructions == |
||
Compass and straightedge |
[[Compass and straightedge construction]]s are known for all known constructible polygons. If ''n'' = ''pq'' with ''p'' = 2 or ''p'' and ''q'' [[coprime]], an ''n''-gon can be constructed from a ''p''-gon and a ''q''-gon. |
||
*If ''p'' = 2, draw a ''q''-gon and [[bisection|bisect]] one of its central angles. From this, a 2''q''-gon can be constructed. |
*If ''p'' = 2, draw a ''q''-gon and [[bisection|bisect]] one of its central angles. From this, a 2''q''-gon can be constructed. |
||
*If ''p'' > 2, inscribe a ''p''-gon and a ''q''-gon in the same circle in such a way that they share a vertex. Because ''p'' and ''q'' are |
*If ''p'' > 2, inscribe a ''p''-gon and a ''q''-gon in the same circle in such a way that they share a vertex. Because ''p'' and ''q'' are coprime, there exists integers ''a'' and ''b'' such that ''ap'' + ''bq'' = 1. Then 2''a'' |
||
Thus one only has to find a compass and straightedge construction for ''n''-gons where ''n'' is a Fermat prime. |
Thus one only has to find a compass and straightedge construction for ''n''-gons where ''n'' is a Fermat prime. |
||
*The construction for an equilateral triangle is simple and has been known since [[Ancient history| |
*The construction for an equilateral [[triangle]] is simple and has been known since [[Ancient history|antiquity]]; see [[Equilateral triangle]]. |
||
*Constructions for the regular pentagon were described both by [[Euclid]] (''[[Euclid's Elements|Elements]]'', ca 300 |
*Constructions for the regular [[pentagon]] were described both by [[Euclid]] (''[[Euclid's Elements|Elements]]'', ca. 300 BC), and by [[Ptolemy]] (''[[Almagest]]'', ca. 150 AD). |
||
*Although Gauss ''proved'' that the regular 17-gon is constructible, he did not actually ''show'' how to do it. The first construction is due to Erchinger, a few years after Gauss' work |
*Although Gauss ''proved'' that the regular [[heptadecagon|17-gon]] is constructible, he did not actually ''show'' how to do it. The first construction is due to Erchinger, a few years after Gauss' work. |
||
*The first explicit |
*The first explicit constructions of a regular [[257-gon]] were given by [[Magnus Georg Paucker]] (1822)<ref>{{cite journal |author=Magnus Georg Paucker |title=Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundersiebenundfünfzig-Ecks in den Kreis |language=German |journal=Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst |volume=2 |year=1822 | pages=160–219|url=https://books.google.com/books?id=aUJRAAAAcAAJ}}</ref> and [[Friedrich Julius Richelot]] (1832).<ref>{{cite journal |author=Friedrich Julius Richelot |title=De resolutione algebraica aequationis x<sup>257</sup> = 1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata |language=Latin |journal=Journal für die reine und angewandte Mathematik |volume=9 |year=1832 | pages=1–26, 146–161, 209–230, 337–358 |url=http://www.digizeitschriften.de/resolveppn/PPN243919689_0009 |doi=10.1515/crll.1832.9.337| s2cid=199545940 }}</ref> |
||
*A construction for a regular 65537-gon was first given by [[Johann Gustav Hermes]] (1894). The construction is very complex; Hermes spent 10 years completing the 200-page manuscript.<ref>{{cite journal | author=Johann Gustav Hermes |title=Über die Teilung des Kreises in 65537 gleiche Teile |language=German |journal=Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse | location=Göttingen | year=1894 |volume=3 |pages=170–186 |url=http://www.digizeitschriften.de/resolveppn/GDZPPN002496585}}</ref> |
*A construction for a regular [[65537-gon]] was first given by [[Johann Gustav Hermes]] (1894). The construction is very complex; Hermes spent 10 years completing the 200-page manuscript.<ref>{{cite journal | author=Johann Gustav Hermes |title=Über die Teilung des Kreises in 65537 gleiche Teile |language=German |journal=Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse | location=Göttingen | year=1894 |volume=3 |pages=170–186 |url=http://www.digizeitschriften.de/resolveppn/GDZPPN002496585}}</ref> |
||
===Gallery=== |
===Gallery=== |
||
[[File:Regular_Pentadecagon_Inscribed_in_a_Circle.gif]] |
|||
[[File:Regular Heptadecagon Using Carlyle Circle.gif|257px]] |
[[File:Regular Heptadecagon Using Carlyle Circle.gif|257px]] |
||
[[File:Regular 257-gon Using Carlyle Circle.gif]] |
[[File:Regular 257-gon Using Carlyle Circle.gif]] |
||
[[File:Regular 65537-gon First Carlyle Circle.gif|257px]]<BR> |
[[File:Regular 65537-gon First Carlyle Circle.gif|257px]]<BR> |
||
From left to right, constructions of a [[heptadecagon|17-gon]], 257-gon and 65537-gon. |
From left to right, constructions of a [[pentadecagon|15-gon]], [[heptadecagon|17-gon]], [[257-gon]] and [[65537-gon]]. Only the first stage of the 65537-gon construction is shown; the constructions of the 15-gon, 17-gon, and 257-gon are given completely. |
||
==Other constructions== |
==Other constructions== |
||
{{see also|Pierpont prime}} |
|||
The concept of constructibility as discussed in this article applies specifically to [[compass and straightedge]] constructions. More constructions become possible if other tools are allowed. The so-called [[neusis construction]]s, for example, make use of a ''marked'' ruler. The constructions are a mathematical idealization and are assumed to be done exactly. |
|||
A regular polygon with ''n'' sides can be constructed with ruler, compass, and [[angle trisection|angle trisector]] if and only if <math>n=2^r3^sp_1p_2\cdots p_k,</math> where ''r, s, k'' ≥ 0 and where the ''p''<sub>''i''</sub> are distinct [[Pierpont prime]]s greater than 3 (primes of the form <math>2^t3^u +1).</math><ref name="Gleason">{{cite journal|last=Gleason|first=Andrew M.|authorlink=Andrew M. Gleason|title=Angle trisection, the heptagon, and the triskaidecagon |journal=[[American Mathematical Monthly]]|date=March 1988|volume=95|issue=3 |pages=185–194 |doi= 10.2307/2323624|jstor=2323624 }}</ref>{{rp|Thm. 2}} These polygons are exactly the regular polygons that can be constructed with [[Conic section]], and the regular polygons that can be constructed with [[Mathematics of paper folding|paper folding]]. The first numbers of sides of these polygons are: |
|||
:3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 24, 26, 27, 28, 30, 32, 34, 35, 36, 37, 38, 39, 40, 42, 45, 48, 51, 52, 54, 56, 57, 60, 63, 64, 65, 68, 70, 72, 73, 74, 76, 78, 80, 81, 84, 85, 90, 91, 95, 96, 97, 102, 104, 105, 108, 109, 111, 112, 114, 117, 119, 120, 126, 128, 130, 133, 135, 136, 140, 144, 146, 148, 152, 153, 156, 160, 162, 163, 168, 170, 171, 180, 182, 185, 189, 190, 192, 193, 194, 195, 204, 208, 210, 216, 218, 219, 221, 222, 224, 228, 234, 238, 240, 243, 247, 252, 255, 256, 257, 259, 260, 266, 270, 272, 273, 280, 285, 288, 291, 292, 296, ... {{OEIS|A122254}} |
|||
==See also== |
==See also== |
||
*[[Polygon]] |
*[[Polygon]] |
||
*[[Carlyle circle]] |
|||
==References== |
==References== |
||
| Line 83: | Line 106: | ||
<references/> |
<references/> |
||
==External links== |
|||
* {{cite journal | author=Duane W. DeTemple |title=Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions | journal=[[The American Mathematical Monthly]] |volume=98 |issue=2 |year=1991 |pages=97–108 |doi=10.2307/2323939 |mr=1089454 |jstor=2323939}} |
* {{cite journal | author=Duane W. DeTemple |title=Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions | journal=[[The American Mathematical Monthly]] |volume=98 |issue=2 |year=1991 |pages=97–108 |doi=10.2307/2323939 |mr=1089454 |jstor=2323939}} |
||
* {{cite journal | author=Christian Gottlieb |title=The Simple and Straightforward Construction of the Regular 257-gon |journal=[[Mathematical Intelligencer]] |volume=21 |issue=1 |year=1999 |pages=31–37 |mr=1665155 | doi=10.1007/BF03024829}} |
* {{cite journal | author=Christian Gottlieb |title=The Simple and Straightforward Construction of the Regular 257-gon |journal=[[Mathematical Intelligencer]] |volume=21 |issue=1 |year=1999 |pages=31–37 |mr=1665155 | doi=10.1007/BF03024829|s2cid=123567824 }} |
||
* [http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html Regular Polygon Formulas], Ask Dr. Math FAQ. |
* [https://web.archive.org/web/20080412084431/http://mathforum.org/dr.math/faq/formulas/faq.regpoly.html Regular Polygon Formulas], Ask Dr. Math FAQ. |
||
| ⚫ | |||
* [http://www.math-cs.ucmo.edu/~mjms/1996.2/clements.ps Why Gauss could not have proved necessity of constructible regular polygons] |
|||
*[https://commons.wikimedia.org/wiki/File:01-65.537-Eck-Quadratrix.svg 65537-gon, exact construction for the 1st side], using the [[Quadratrix of Hippias]] and [[GeoGebra]] as additional aids, with brief description (German) |
|||
| ⚫ | |||
[[Category: |
[[Category:Constructible polygons| ]] |
||
[[Category:Euclidean plane geometry]] |
[[Category:Euclidean plane geometry]] |
||
[[Category:Carl Friedrich Gauss]] |
|||
[[ar:مضلع قابل للإنشاء]] |
|||
[[ca:Polígon construïble]] |
|||
[[de:Konstruierbare Polygone]] |
|||
[[es:Polígono construible]] |
|||
[[fr:Théorème de Gauss-Wantzel]] |
|||
[[hu:Szerkeszthető sokszögek]] |
|||
[[pl:Twierdzenie Gaussa-Wantzela]] |
|||
[[ru:Теорема Гаусса — Ванцеля]] |
|||
[[th:รูปหลายเหลี่ยมสร้างได้]] |
|||
[[uk:Теорема Гауса - Ванцеля]] |
|||
[[zh: |
|||
Revision as of 18:50, 28 April 2024

In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinitely many constructible polygons, but only 31 with an odd number of sides are known.
Conditions for constructibility

Some regular polygons are easy to construct with compass and straightedge; others are not. The ancient Greek mathematicians knew how to construct a regular polygon with 3, 4, or 5 sides,[1]: p. xi and they knew how to construct a regular polygon with double the number of sides of a given regular polygon.[1]: pp. 49–50 This led to the question being posed: is it possible to construct all regular polygons with compass and straightedge? If not, which n-gons (that is, polygons with n edges) are constructible and which are not?
Carl Friedrich Gauss proved the constructibility of the regular 17-gon in 1796. Five years later, he developed the theory of Gaussian periods in his Disquisitiones Arithmeticae. This theory allowed him to formulate a sufficient condition for the constructibility of regular polygons. Gauss stated without proof that this condition was also necessary,[2] but never published his proof.
A full proof of necessity was given by Pierre Wantzel in 1837. The result is known as the Gauss–Wantzel theorem: A regular n-gon can be constructed with compass and straightedge if and only if n is the product of a power of 2 and any number of distinct Fermat primes. Here, a power of 2 is a number of the form , where m ≥ 0 is an integer. A Fermat prime is a prime number of the form , where m ≥ 0 is an integer. The number of Fermat primes involved can be 0, in which case n is a power of 2.
In order to reduce a geometric problem to a problem of pure number theory, the proof uses the fact that a regular n-gon is constructible if and only if the cosine is a constructible number—that is, can be written in terms of the four basic arithmetic operations and the extraction of square roots. Equivalently, a regular n-gon is constructible if any root of the nth cyclotomic polynomial is constructible.
Detailed results by Gauss's theory
Restating the Gauss–Wantzel theorem:
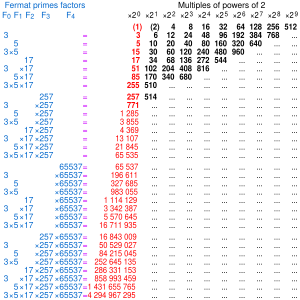
- A regular n-gon is constructible with straightedge and compass if and only if n = 2kp1p2...pt where k and t are non-negative integers, and the pi's (when t > 0) are distinct Fermat primes.
The five known Fermat primes are:
Since there are 31 nonempty subsets of the five known Fermat primes, there are 31 known constructible polygons with an odd number of sides.
The next twenty-eight Fermat numbers, F5 through F32, are known to be composite.[3]
Thus a regular n-gon is constructible if
- n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, ... (sequence A003401 in the OEIS),
while a regular n-gon is not constructible with compass and straightedge if
- n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 31, 33, 35, 36, 37, 38, 39, 41, 42, 43, 44, 45, 46, 47, 49, 50, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 65, 66, 67, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 81, 82, 83, 84, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 97, 98, 99, 100, 101, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122, 123, 124, 125, 126, 127, ... (sequence A004169 in the OEIS).
Connection to Pascal's triangle
Since there are 5 known Fermat primes, we know of 31 numbers that are products of distinct Fermat primes, and hence 31 constructible odd-sided regular polygons. These are 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295 (sequence A045544 in the OEIS). As John Conway commented in The Book of Numbers, these numbers, when written in binary, are equal to the first 32 rows of the modulo-2 Pascal's triangle, minus the top row, which corresponds to a monogon. (Because of this, the 1s in such a list form an approximation to the Sierpiński triangle.) This pattern breaks down after this, as the next Fermat number is composite (4294967297 = 641 × 6700417), so the following rows do not correspond to constructible polygons. It is unknown whether any more Fermat primes exist, and it is therefore unknown how many odd-sided constructible regular polygons exist. In general, if there are q Fermat primes, then there are 2q−1 odd-sided regular constructible polygons.
General theory
In the light of later work on Galois theory, the principles of these proofs have been clarified. It is straightforward to show from analytic geometry that constructible lengths must come from base lengths by the solution of some sequence of quadratic equations.[4] In terms of field theory, such lengths must be contained in a field extension generated by a tower of quadratic extensions. It follows that a field generated by constructions will always have degree over the base field that is a power of two.
In the specific case of a regular n-gon, the question reduces to the question of constructing a length
- cos 2
π /n ,
which is a trigonometric number and hence an algebraic number. This number lies in the n-th cyclotomic field — and in fact in its real subfield, which is a totally real field and a rational vector space of dimension
- ½
φ (n),
where
As for the construction of Gauss, when the Galois group is a 2-group it follows that it has a sequence of subgroups of orders
- 1, 2, 4, 8, ...
that are nested, each in the next (a composition series, in group theory terminology), something simple to prove by induction in this case of an abelian group. Therefore, there are subfields nested inside the cyclotomic field, each of degree 2 over the one before. Generators for each such field can be written down by Gaussian period theory. For example, for n = 17 there is a period that is a sum of eight roots of unity, one that is a sum of four roots of unity, and one that is the sum of two, which is
- cos 2
π /17 .
Each of those is a root of a quadratic equation in terms of the one before. Moreover, these equations have real rather than complex roots, so in principle can be solved by geometric construction: this is because the work all goes on inside a totally real field.
In this way the result of Gauss can be understood in current terms; for actual calculation of the equations to be solved, the periods can be squared and compared with the 'lower' periods, in a quite feasible algorithm.
Compass and straightedge constructions
Compass and straightedge constructions are known for all known constructible polygons. If n = pq with p = 2 or p and q coprime, an n-gon can be constructed from a p-gon and a q-gon.
- If p = 2, draw a q-gon and bisect one of its central angles. From this, a 2q-gon can be constructed.
- If p > 2, inscribe a p-gon and a q-gon in the same circle in such a way that they share a vertex. Because p and q are coprime, there exists integers a and b such that ap + bq = 1. Then 2a
π /q + 2bπ /p = 2π /pq. From this, a pq-gon can be constructed.
Thus one only has to find a compass and straightedge construction for n-gons where n is a Fermat prime.
- The construction for an equilateral triangle is simple and has been known since antiquity; see Equilateral triangle.
- Constructions for the regular pentagon were described both by Euclid (Elements, ca. 300 BC), and by Ptolemy (Almagest, ca. 150 AD).
- Although Gauss proved that the regular 17-gon is constructible, he did not actually show how to do it. The first construction is due to Erchinger, a few years after Gauss' work.
- The first explicit constructions of a regular 257-gon were given by Magnus Georg Paucker (1822)[5] and Friedrich Julius Richelot (1832).[6]
- A construction for a regular 65537-gon was first given by Johann Gustav Hermes (1894). The construction is very complex; Hermes spent 10 years completing the 200-page manuscript.[7]
Gallery




From left to right, constructions of a 15-gon, 17-gon, 257-gon and 65537-gon. Only the first stage of the 65537-gon construction is shown; the constructions of the 15-gon, 17-gon, and 257-gon are given completely.
Other constructions
The concept of constructibility as discussed in this article applies specifically to compass and straightedge constructions. More constructions become possible if other tools are allowed. The so-called neusis constructions, for example, make use of a marked ruler. The constructions are a mathematical idealization and are assumed to be done exactly.
A regular polygon with n sides can be constructed with ruler, compass, and angle trisector if and only if where r, s, k ≥ 0 and where the pi are distinct Pierpont primes greater than 3 (primes of the form [8]: Thm. 2 These polygons are exactly the regular polygons that can be constructed with Conic section, and the regular polygons that can be constructed with paper folding. The first numbers of sides of these polygons are:
- 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 24, 26, 27, 28, 30, 32, 34, 35, 36, 37, 38, 39, 40, 42, 45, 48, 51, 52, 54, 56, 57, 60, 63, 64, 65, 68, 70, 72, 73, 74, 76, 78, 80, 81, 84, 85, 90, 91, 95, 96, 97, 102, 104, 105, 108, 109, 111, 112, 114, 117, 119, 120, 126, 128, 130, 133, 135, 136, 140, 144, 146, 148, 152, 153, 156, 160, 162, 163, 168, 170, 171, 180, 182, 185, 189, 190, 192, 193, 194, 195, 204, 208, 210, 216, 218, 219, 221, 222, 224, 228, 234, 238, 240, 243, 247, 252, 255, 256, 257, 259, 260, 266, 270, 272, 273, 280, 285, 288, 291, 292, 296, ... (sequence A122254 in the OEIS)
See also
References
- ^ a b Bold, Benjamin. Famous Problems of Geometry and How to Solve Them, Dover Publications, 1982 (orig. 1969).
- ^ Gauss, Carl Friedrich (1966). Disquisitiones arithmeticae. New Haven and London: Yale University Press. pp. 458–460. Retrieved 25 January 2023.
- ^ Prime factors k · 2n + 1 of Fermat numbers Fm and complete factoring status by Wilfrid Keller.
- ^ Cox, David A. (2012), "Theorem 10.1.6", Galois Theory, Pure and Applied Mathematics (2nd ed.), John Wiley & Sons, p. 259, doi:10.1002/9781118218457, ISBN 978-1-118-07205-9.
- ^ Magnus Georg Paucker (1822). "Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundersiebenundfünfzig-Ecks in den Kreis". Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst (in German). 2: 160–219.
- ^ Friedrich Julius Richelot (1832). "De resolutione algebraica aequationis x257 = 1, sive de divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata". Journal für die reine und angewandte Mathematik (in Latin). 9: 1–26, 146–161, 209–230, 337–358. doi:10.1515/crll.1832.9.337. S2CID 199545940.
- ^ Johann Gustav Hermes (1894). "Über die Teilung des Kreises in 65537 gleiche Teile". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (in German). 3. Göttingen: 170–186.
- ^ Gleason, Andrew M. (March 1988). "Angle trisection, the heptagon, and the triskaidecagon". American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. JSTOR 2323624.
External links
- Duane W. DeTemple (1991). "Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions". The American Mathematical Monthly. 98 (2): 97–108. doi:10.2307/2323939. JSTOR 2323939. MR 1089454.
- Christian Gottlieb (1999). "The Simple and Straightforward Construction of the Regular 257-gon". Mathematical Intelligencer. 21 (1): 31–37. doi:10.1007/BF03024829. MR 1665155. S2CID 123567824.
- Regular Polygon Formulas, Ask Dr. Math FAQ.
- Carl Schick: Weiche Primzahlen und das 257-Eck : eine analytische Lösung des 257-Ecks. Zürich : C. Schick, 2008. ISBN 978-3-9522917-1-9.
- 65537-gon, exact construction for the 1st side, using the Quadratrix of Hippias and GeoGebra as additional aids, with brief description (German)





