Octahedron

Octahedron
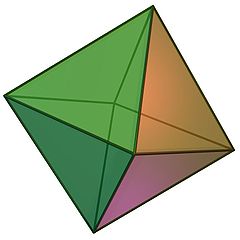Click on picture for large version. Click here for spinning version.
Type	Platonic
Faces	8 triangles
Edges	12
Vertices	6
Vertex configuration	3.3.3.3
Symmetry group	octahedral (Oh) of order 48
Dual polyhedron	Regular cube Rhombic rhombohedron
Dihedral angle	109.47122° = arccos(-1/3)
Properties	regular, convex, deltahedron
Vertex Figure

An octahedron (plural: octahedra) is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight faces each of which is an equilateral triangle four of which meet at each vertex. The regular octahedron is a special kind of triangular antiprism and of square bipyramid, and is dual to the cube.

Polygonal net

The octahedron in general

There are four import topological types of octahedra with dihedral symmetry:

• Hexagonal prism 6 triangles, 2 hexagons
• Septagonal pyramid - 7 triangles, 1 septagon
• Tetragonal bipyramid - 8 triangles, usually isosceles)
  • The regular octahedron is a special case with equilateral triangles
• Tetragonal trapezohedron - 8 kites

In the general meaning the term octahedron it is not much used because of these different types which have not much in common except having the same number of faces.

Canonical coordinates

Canonical coordinates for the vertices of a regular octahedron centered at the origin are (±1,0,0), (0,±1,0), (0,0,±1).

Area and volume

The area A and the volume V of a regular octahedron of edge length a are:

$A=2{\sqrt {3}}a^{2}$

$V={\begin{matrix}{1 \over 3}\end{matrix}}{\sqrt {2}}a^{3}$

Thus the volume is four times that of a regular tetrahedron with the same edge length, while the surface area is twice (because we have 8 vs. 4 triangles).

Geometric relations

The interior of the compound of two dual tetrahedra is an octahedron, and this compound, called the stella octangula, is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids. One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of an icosahedron. There are five octahedra that define any given icosahedron in this fashion, and together they define a regular compound.

Octahedra and tetrahedra can be mixed together to form a vertex, edge, and face-uniform tiling of space, called the octet truss by Buckminster Fuller. This is the only such tiling save the regular tessellation of cubes, and is one of the 28 Andreini tessellations. Another is a tessellation of octahedra and cuboctahedra.

The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess mirror planes that do not pass through any of the faces.

Using the standard nomenclature for Johnson solids, an octahedron would be called a square bipyramid.

Uses

Especially in roleplaying, this solid is known as a d8, one of the more common Polyhedral dice.

If each edge of an octahedron is replaced by a one ohm resistor, the resistance between opposite vertices is 0.5 ohms, and that between adjacent vertices 5/12 ohms.

See also

• Triakis octahedron
• Hexakis octahedron
• Truncated octahedron

External links

• Octahedron - Mathworld.com
• Spinning Octahedron - MathsIsFun.com
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Paper Models of Polyhedra Many links