Balentzia loturaren teoria

Kimikan, balentzia loturaren teoria, orbital molekularren teoriarekin batera, mekanika kuantikoaren metodoak erabiliz, molekulen propietateak azaltzeko, lotura kimikoa horien artean, garatu ziren teoriak dira. Balentzia loturaren teorian, ondoan dauden atomoen orbital atomikoak konbinatzean orbital molekularrak sortzen dira, Lewisen ereduan oinarrituta. Horrela, orbital molekular lokalizatuak dira teoria honen oinarrietako bat. Orbital molekularren teoriak, bestalde, molekula osoan sortutako orbital molekularrak hartzen ditu kontuan.^[1]

Historia

1916. urtean, G. N. Lewisek proposatu zuen lotura kimikoa partekatutako bi elektroien arteko interakzioaren ondorioz sortzen dela, molekulak Lewisen egituraz adieraziz. Teoria kuantikoaren garapenarekin batera, 1927an, Heiter-London teoria aurkeztu zen. Teoria honek ahalbidetu zuen, lehen aldiz, hidrogeno molekularen H₂ lotura propietateen kalkulua mekanika kuantika oinarritzat hartuz. Walter Heitlerek adierazi zuen nola erabili Schrödingerren uhin ekuazioa bi hidrogeno atomoen uhin funtzioak batu eta lotura kobalentea emateko. Ondoren Fritz London lankidea deitu eta teoriaren berezitasunetan lan egin zuten^[2]. Beranduago, Linus Paulingek, Lewisen elektroi pare lotzailea, eta, Heiter-London teoriak, erabili zituen balentzia lotura teoriaren bi aspektu garatzeko; erresonantzia (1928) eta orbitalen hibridazioa (1930). Azkeneko aurrerapen horiek guztiek hasiera eman zioten balentzia loturaren teoria berriari, non oinarria uhin-mekanika zen.

Born-Oppenheimerren hurbilketa

Edozein sistema kuantikoetan bezala, molekulei buruzko informazioa lortzeko Schrödinger ekuazioa ebatzi behar da. Egoera geldikorren kasuan, denborarekiko independientea den ekuazioa: $\operatorname {\hat {H}} \Psi =E\Psi$ . Ekuazio hau ebatziz sistemaren energia eta informazio guztia duen uhinfuntzioa lortuko dira. Kasu honetan, eta molekulak aztertzen ari garenez, Hamiltondar operadoreak hainbat osagai izango ditu bere barruan; nukleoen energia zinetikoa, ${\hat {T}}_{N}$ , elektroien energia zinetikoa, ${\hat {T}}_{e}$ , elektroi eta nukleo arteko energia potentziala, ${\hat {V}}_{eN}$ , nukleoen arteko energia potentziala, ${\hat {V}}_{NN}$ , eta elektroien arteko energia potentziala, ${\hat {V}}_{ee}$ .

Beraz, molekularen ezaugarriak ezagutzeko hurrengo Hamiltondarra erabili beharko litzateke:

{\hat {H}}={\hat {T}}_{N}+{\hat {T}}_{e}+{\hat {V}}_{eN}+{\hat {V}}_{NN}+{\hat {V}}_{ee}

Hala ere, operadore honekin gelditzen den ekuazioa zehaztasunez ebaztea ezinezkoa da eta horregatik, Born-Oppenheimerren hurbilketa erabiltzen da ekuazioa ebazteko, modu hurbilduan bada ere. Hurbilketa honetan, elektroien eta nukleoen mugimendua desakoplatua dagoela suposatzen da, eta horren ondorioz, elektroien eta nukleoen menpe dauden operadoreak banatu egingo dira, ondoren adierazten diren ekuazio sinpleagoak lortuz:

Elektroien menpeko ekuazioa:

{{\hat {H}}_{e}}\Psi _{e}=E_{e}\Psi _{e}

Nukleoen menpeko ekuazioa:

{{\hat {H}}_{N}}\Psi _{N}=E_{Tot}\Psi _{N}

Ekuazio elektronikoa ezin da zehaztasun osoz ebatzi bi elektroi baino gehiagoko kasuetarako. Horrela, ekuazio hori ebazteko hurbilketa gehiago egin behar dira, eta hurbilketa horietako bat balentzia loturaren teoria da.

Teoria

Teoria honek azaltzen duenez, bi atomoren elektroi desparekatudun balentzi orbitalen arteko gainezarpena ematen denean sortzen da lotura kobalentea. Gainezarpena gero eta handiagoa izan, loturaren sendotasuna handiagoa izango da. Balentzi lotura baten egitura, Lewis egituraren antzekoa da, baina Lewis egitura bakarraren bidez irudikatu ezin daitekeena, hainbat balentzi loturaren egituren bidez azaltzen da. Balentzi loturaren egitura hauetako bakoitzak Lewis egitura zehatz bat adierazten du. Balentzi loturen konbinazioak dira Erresonantzia teoriaren atal nagusia. Balentzi loturaren teoriak kontsideratzen du gainezarpenean parte hartzen duten atomoetako orbital bakoitzak osatzen duela lotura kimikoa. Gainezarpenaren ondorioz, elektroia aurkitzeko probabilitate handiena, loturaren zonaldean dago. Balentzia loturaren teoriaren ikuspuntutik, lotura bat, bi orbitalen arteko gainezarpen txikia eta ahula da. Orokorrean, Balentzi loturaren teoria errazagoa da aplikatzen, oinarrizko egoeran dauden molekulei. Balentzi orbital eta balentzi elektroiak ez direnek, ez dute aldaketarik jasaten loturen eraketan.

Orbital atomikoen arteko gainezarpenak ezberdinak izan daitezke. Bi moduak sigma (σしぐま) eta pi (πぱい) gainezarpenak dira. Sigma (σしぐま) lotura ematen da, orbitalen gainezarpena aurrez aurrekoa denean. Pi (πぱい) loturak berriz, gainezarpen paraleloa ematen denean ematen dira. Adibidez, bi S orbitaleko elektroien arteko lotura beti izango da sigma (σしぐま) lotura, orbital horien arteko gainezarpena beti izango baita koaxiala. Lotura ordenari dagokionez, lotura bakunak sigma (σしぐま) lotura bakarra izango du, lotura bikoitzak, sigma (σしぐま) eta pi (πぱい) lotura bat, eta hirukoitzak aldiz, sigma (σしぐま) bakarra eta bi pi (σしぐま) lotura izango ditu. Hala ere, loturetan parte hartzen dutenean, orbital atomikoak hibridoak (ezberdinak) izan daitezke. Askotan, loturetako orbital atomikoek orbital mota ezberdinen izaerak erakusten dituzte. Prozesu honi, hau da, orbital atomiko batek beharrezkoak diren ezaugarriak lortzeari, hibridazioa deritzo.

Balentzia loturaren teoria, gaur egun

Gaur egun, balentzia loturaren teoriak orbital molekularraren teoria osatzen du, baina ez dio gehitzen balentzia loturaren teoriari, elektroi pareak bi atomo espezifikoen artean kokatzen direla, baina banatuak daudela orbital molekularretan, molekula osoan zehar zabaldu daitezkeenak. Orbital molekularraren teoriak propietate magnetikoak (diamagnetismoa/paramagnetismoa) eta ionikoak aurresan ditzake modu zuzen batean. Balentzia loturaren teoria erabilita ordea, antzeko emaitzak lortzen dira modu zailago batean. Balentzia loturaren teoriaren arabera molekula aromatikoen propietateak πぱい orbitalen biraketen akoplamenduaren ondorio dira (Kekulé, Dewar egituren erresonantziaren ondorioa) eta orbital molekularraren arabera, propietate horiek ematen dira πぱい elektroien deslekutzearen ondorioz^[3]^[4]^[5]^[6]. Balentzia loturaren teoria murriztua dago molekula txikitara, lotura balentzien orbitalen ortogonalitate faltagatik, eta, lotura balentzien egituragatik. Orbital molekularrak ordea, guztiz ortogonalak dira. Bestalde, balentzia loturaren teoria erabiliz, argi ikus daiteke karga elektronikoaren berantolaketa erreakzio kimikoetan loturak sortu eta apurtzerako garaian. Esan dezakegu teoria honek ongi aurresaten duela molekula diatomiko homonuklearren disoziazioa atomo ezberdinetan, orbital molekularraren teoriak ordea, aurresaten du, atomo eta ioiez osaturiko nahasteen disoziazioa. Balentzia loturaren teoria modernoak,ordezkatu egingo du orbital atomikoen gainjartzea lotura balentzien orbitalen gainjartzearekin, molekula osoan zehar zabaltzen direnak. Korrelazio energetikoa jartzerakoan, energia erresultanteak konpetitiboagoak izango dira hartree fock uhin funtzioen erreferentziengatik^[7].

Balentzia loturaren teoriaren adibide batzuk

Balentzia loturaren teoriak aurresandako orbital-diagrama bentzeno molekularen πぱい-sistemarentzat.

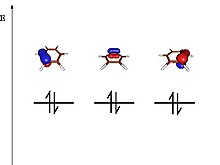
Irudietan ikus daitekeen moduan, Balentzia loturaren teoriaren bidez lortzen diren orbitalak, bi atomoren artean kokatzen dira; hau da, ez dira molekula osoan zehar deslokalizatuta dauden orbitalak lortzen, Orbital molekularren teoriak aurresango lukeenez. Horrez gain, Balentzia loturaren teoriari esker, jakin dezakegu zein izango den orbitalen arteko gainjartze maximoa. Hau dela eta, jakin dezakegu zein den sortu daitekeen lotura sendoena. Modu honetan, azaldu daitezke, sortzen diren lotura kobalente ugari.

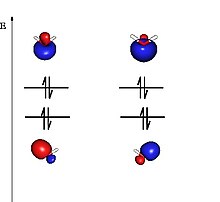
CH₄ molekulan, lau karbono hidrogeno lotura sortzen dira. Karbonoak hibridazioa jasaten du eta lau sp³ orbital hibrido osatzen ditu. Orbital hibrido bakoitzean, elektroi bat kokatzen da eta hidrogenoaren 1s orbitalekin lau lotura kobalente osatzen dira. H₂ molekulan, lotura sortzen duten orbitalen ezaugarriak ezberdinak direnez, lotura-luzera eta lotura-indarra aldatuko dira batetik bestera.

Bentzenoaren kasuan berriz, πぱい-loturak binaka osatzen dira karbonoen p-orbitalen gainezarpenaren ondorioz hiru πぱい-lotura finko osatuz. Hasieran proposatutako egitura honek datu esperimentalekin bat egiten ez zuela ikusita, erresonantzi kontzeptua txertatu zen Balentzia loturaren teorian. Honen ondorioz, sei atomoetan deslokalizatutako hiru πぱい-lotura lortzen dira.

Erreferentziak

↑ Murrel, J.N.; Kettle, S.F.A.; Tedder, J.M. (1985). The Chemical Bond (2nd ed.). John Wiley & Sons. ISBN 0-471-90759-6
↑ Walter Heitler– Key participants in the development of Linus Pauling's The Nature of the Chemical Bond
↑ Cooper, David L.; Gerratt, Joseph; Raimondi, Mario (1986). The electronic structure of the benzene molecule. Nature. 323 (6090): 699. Bibcode:1986Natur.323..699C. doi:10.1038/323699a0
↑ Pauling, Linus (1987). Electronic structure of the benzene molecule. Nature. 325 (6103): 396. Bibcode:1987Natur.325..396P. doi:10.1038/325396d0
↑ Messmer, Richard P.; Schultz, Peter A. (1987). The electronic structure of the benzene molecule. Nature. 329 (6139): 492. Bibcode:1987Natur.329..492M. doi:10.1038/329492a0
↑ Harcourt, Richard D. (1987). The electronic structure of the benzene molecule. Nature. 329 (6139): 491. Bibcode:1987Natur.329..491H. doi:10.1038/329491b0
↑ Shaik, Sason S.; Phillipe C. Hiberty (2008). A Chemist's Guide to Valence Bond Theory. New Jersey: Wiley-Interscience. ISBN 978-0-470-03735-5

Kanpo estekak

Datuak: Q517973

[1] Murrel, J.N.; Kettle, S.F.A.; Tedder, J.M. (1985). The Chemical Bond (2nd ed.). John Wiley & Sons. ISBN 0-471-90759-6

[2] Walter Heitler– Key participants in the development of Linus Pauling's The Nature of the Chemical Bond

[3] Cooper, David L.; Gerratt, Joseph; Raimondi, Mario (1986). The electronic structure of the benzene molecule. Nature. 323 (6090): 699. Bibcode:1986Natur.323..699C. doi:10.1038/323699a0

[4] Pauling, Linus (1987). Electronic structure of the benzene molecule. Nature. 325 (6103): 396. Bibcode:1987Natur.325..396P. doi:10.1038/325396d0

[5] Messmer, Richard P.; Schultz, Peter A. (1987). The electronic structure of the benzene molecule. Nature. 329 (6139): 492. Bibcode:1987Natur.329..492M. doi:10.1038/329492a0

[6] Harcourt, Richard D. (1987). The electronic structure of the benzene molecule. Nature. 329 (6139): 491. Bibcode:1987Natur.329..491H. doi:10.1038/329491b0

[7] Shaik, Sason S.; Phillipe C. Hiberty (2008). A Chemist's Guide to Valence Bond Theory. New Jersey: Wiley-Interscience. ISBN 978-0-470-03735-5

[1]

[2]

[3]

[4]

[5]

[6]

[7]