AnglePath[{
{0,0}から
AnglePath[{{r1,
AnglePath[
![]()
AnglePath[{x,y},{step1,step2,…}]
![]()
AnglePath[{{x,y},
![]()
AnglePath[{{x,y},{dx,dy}},{step1,step2,…}]
{x,y}から{x+dx,y+dy}へ
AnglePath[init,steps,form]


AnglePath
AnglePath[{
{0,0}から
AnglePath[{{r1,
AnglePath[
![]()
AnglePath[{x,y},{step1,step2,…}]
![]()
AnglePath[{{x,y},
![]()
AnglePath[{{x,y},{dx,dy}},{step1,step2,…}]
{x,y}から{x+dx,y+dy}へ
AnglePath[init,steps,form]
詳細 とオプション


- AnglePathは,
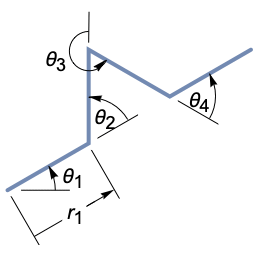
経路 の形成 で達 した各 点 で,事実 上 ,まず指定 された相対 角度 で回転 し,次 に指定 された距離 を進 む. - Quantityオブジェクトとして
明示 的 に与 えられない限 り,角度 θ iは,ラジアン単位 で反 時計 回 りに大 きくなるとみなされる(Degreeをかけて度 から変換 することができる). - AnglePath[{
θ 1,θ 2,θ 3,…}]では,角度 θ 1は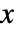
軸 と相対 的 であるとみなされる. - AnglePath[…,form]の form には
以下 を使 うことができる. -
"Position" 直交 座標 {xi,yi}(デフォルト)"FrameMatrix" 現行 フレームの初期 フレームに対 する回転 行列 "RelativeMatrix" 現行 フレームの以前 のフレームに対 する回転 行列 "FrameAngle" 初期 ステップに対 する回転 角 "RelativeAngle" 以前 のステップに対 する回転 角 "Translation" 初期 ステップからの平行 移動 変換 "Rotation" 初期 ステップからの回転 変換 "RotationTranslation" 初期 ステップからの回転 平行 移動 変換 {form1,form2,…} 形 のリスト - AnglePathの
引数 は記号 的 なものでよい.また,Quantityオブジェクトでもよい. - AnglePathには,
生成 された数 の精度 を決定 するWorkingPrecisionオプションが使 える. - デフォルト
設定 のWorkingPrecisionAutomaticでは,比較的 パスが短 い場合 にのみ,厳密 な入力 に対 しては厳密 数 が生成 される.パスが長 い場合 には機械 精度 が使 われる.
関連 するガイド
-
▪
-
反復 写像 とフラクタル
▪
-
計算 系
▪
-
角度 と極座標
テキスト
Wolfram Research (2015), AnglePath, Wolfram
CMS
Wolfram Language. 2015. "AnglePath." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/AnglePath.html.
APA
Wolfram Language. (2015). AnglePath. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AnglePath.html
BibTeX
@misc{reference.wolfram_2025_anglepath, author="Wolfram Research", title="{AnglePath}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/AnglePath.html}", note=[Accessed: 18-August-2025]}
BibLaTeX
@online{reference.wolfram_2025_anglepath, organization={Wolfram Research}, title={AnglePath}, year={2019}, url={https://reference.wolfram.com/language/ref/AnglePath.html}, note=[Accessed: 18-August-2025]}